문제 출처 : https://www.acmicpc.net/problem/9370
난이도 : 골드 2

문제 파악

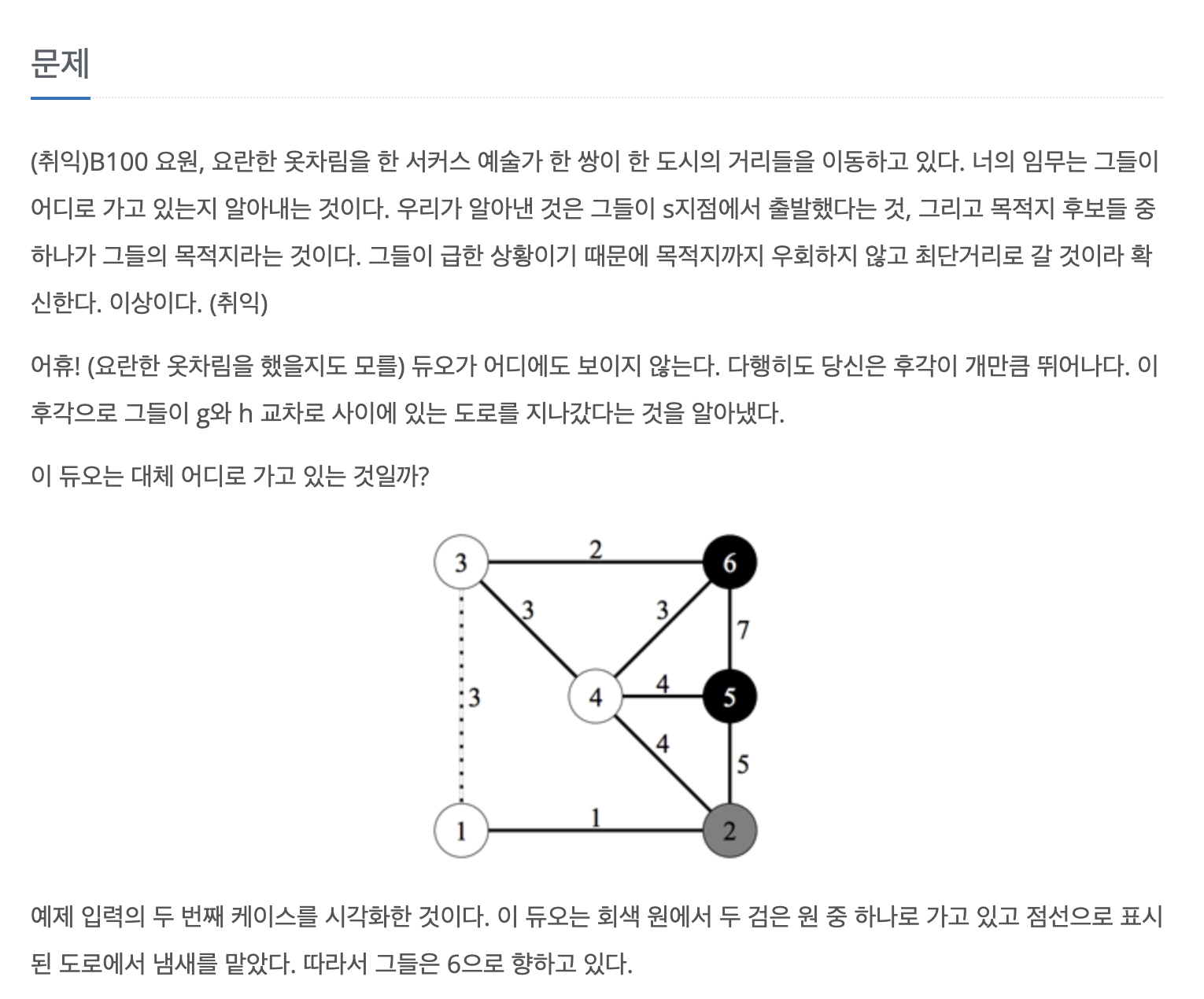
출발지 s에서 여러 목적지 후보 x들 중, 최단경로 중에 반드시 g-h 간선을 지나가는 후보만 골라 출력하는 문제다.

이전에 풀었던 백준 1504번: 특정한 최단경로 문제가 도움이 되었다.

출발지 s -> 목적지 후보 x 사이에 g-h or h-g 경로가 있어야 하기에

s-> g-> h-> x
or
s-> h-> g-> x 의 최단경로 수가

다이렉트 s-> x 와 같다면 찾고 있는 진짜 목적지 후보가 된다.

이전 1504번 문제 처럼 다익스트라 3번을 돌려 출발지가 각각 s, g, h 인 거리배열을 만들어 풀 수 있다.

해답 및 풀이

import sys
import heapq
input = sys.stdin.readline

INF = 10**15

def dijkstra(start, graph, n):
    dist = [INF] * (n + 1)
    dist[start] = 0
    pq = [(0, start)]
    while pq:
        cost, node = heapq.heappop(pq)
        if cost > dist[node]:
            continue
        for nxt, w in graph[node]:
            ncost = cost + w
            if ncost < dist[nxt]:
                dist[nxt] = ncost
                heapq.heappush(pq, (ncost, nxt))
    return dist

T = int(input())
for _ in range(T):
    n, m, t = map(int, input().split())
    s, g, h = map(int, input().split())

    graph = [[] for _ in range(n + 1)]
    wGH = None

    for _ in range(m):
        a, b, d = map(int, input().split())
        graph[a].append((b, d))
        graph[b].append((a, d))
        if (a == g and b == h) or (a == h and b == g):
            wGH = d

    candidates = [int(input()) for _ in range(t)]
    candidates.sort()

    distS = dijkstra(s, graph, n)
    distG = dijkstra(g, graph, n)
    distH = dijkstra(h, graph, n)

    ans = []
    for x in candidates:
        if distS[x] == INF:
            continue

        path1 = distS[g] + wGH + distH[x]  # s -> g -> h -> x
        path2 = distS[h] + wGH + distG[x]  # s -> h -> g -> x

        if distS[x] == path1 or distS[x] == path2:
            ans.append(x)

    print(*ans)