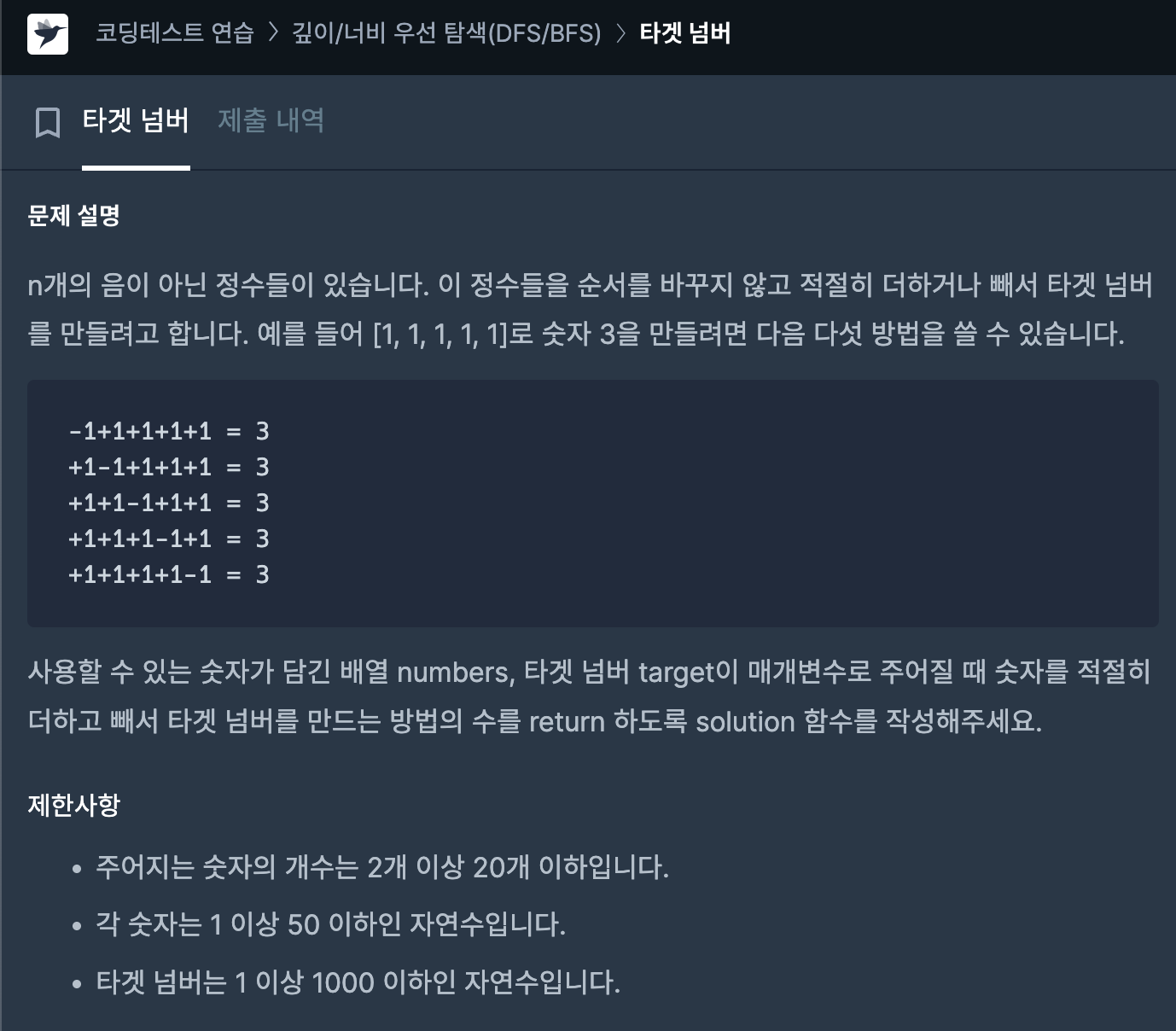
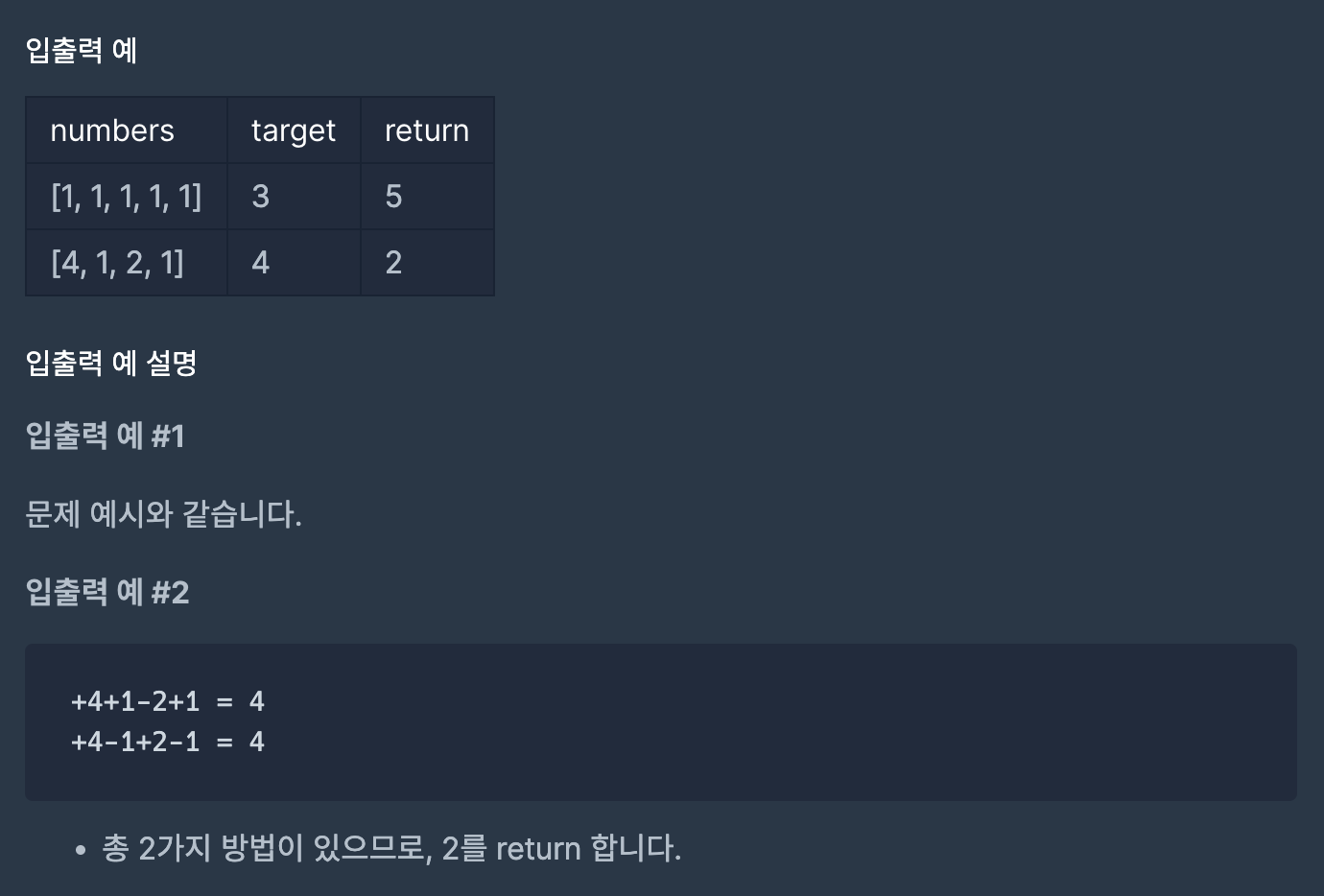
문제 출처 : https://school.programmers.co.kr/learn/courses/30/lessons/43165
난이도 : Level 2

---

문제 파악

numbers에 있는 숫자들을 순서대로 보면서, 각 숫자 앞에 +를 붙일지 -를 붙일지 선택한다.
모든 선택을 끝까지 했을 때 만들어진 합이 target이면 그 경우를 세면 된다.

예를 들어 numbers가 [1, 1, 1]이면, 각 숫자마다 선택지가 2개(+ 또는 -)라서 전체 경우의 수는 2^3 = 8개다.
이 8개를 전부 검사하면 되는데, 이 “선택을 하나씩 내려가며 끝까지 가는 방식”이기에 DFS(깊이 우선 탐색) 을 활용하면 좋을 것 같다.

---

DFS로 푼다는 건 “상태를 들고 내려간다”는 뜻이다.

그렇다면 어떤 상태를 들고 내려가야 할까?

1. idx : 지금 몇 번째 숫자를 처리 중인지
2. total : 지금까지 만든 누적합이 얼마인지

dfs(idx, total)
= idx번째 숫자부터 선택을 계속해서, 최종적으로 target을 만드는 경우의 수

---

종료 조건은 끝까지 다 선택했을 때 가 되시겠다.

중간에 target과 같아도 끝난 게 아니다.
모든 숫자에 +/−를 다 붙여야 “하나의 완성된 경우”가 된다.

그래서 종료 조건은:
idx == len(numbers) (모든 숫자를 다 사용했다)
total == target이면 경우의 수 1, 아니면 0

재귀(다음으로 내려가는 방법)는 항상 2갈래이다.

더하기: total + numbers[idx]
빼기: total - numbers[idx]

그리고 idx는 다음 숫자로 넘어가니까 idx + 1.
즉:
dfs(idx+1, total + numbers[idx])
dfs(idx+1, total - numbers[idx])

해답 및 풀이

def solution(numbers,target):
    
    n = len(numbers)
    
    def dfs(idx, total):
        if idx == n:
            return 1 if total == target else 0
        
        return dfs(idx+1, total + numbers[idx]) + dfs(idx+1, total - numbers[idx])
    
    return dfs(0,0)

사실 이 문제를 네달전에도 풀었었다.
그때는 재귀로 푸는 것이 너무 와닿지 않아 BFS로 풀었는데
지금은 재귀가 조금은 와닿는 것 같아 DFS로 접근했는데 더 적절한 코드인 듯 하다.

사실 조금 더 친절한 코드는 또 다음 코드로 볼 수 있다.

def solution(numbers, target):
    n = len(numbers)
    count = 0

    def dfs(idx, total):
        nonlocal count # 바깥 함수(상위 함수)의 지역변수
 
        # 모든 숫자 다 썼으면 결과 체크
        if idx == n:
            if total == target:
                count += 1
            return

        # 이번 숫자를 +로 쓰는 경우
        dfs(idx + 1, total + numbers[idx])
        # 이번 숫자를 -로 쓰는 경우
        dfs(idx + 1, total - numbers[idx])

    dfs(0, 0)
    return count

---

다음날 풀어본 코드

def solution(numbers,target):
    n = len(numbers)
    
    def dfs(idx, total):
        # 종료 조건
        if idx == n:
            if total == target:
                return 1
            else:
                return 0
        
        return dfs(idx+1, total + numbers[idx]) + dfs(idx+1, total - numbers[idx])
    
    return dfs(0,0)