프로그래머스 Level 3 | 정수 삼각형 | Python 풀이

https://school.programmers.co.kr/learn/courses/30/lessons/43105

---

문제 파악

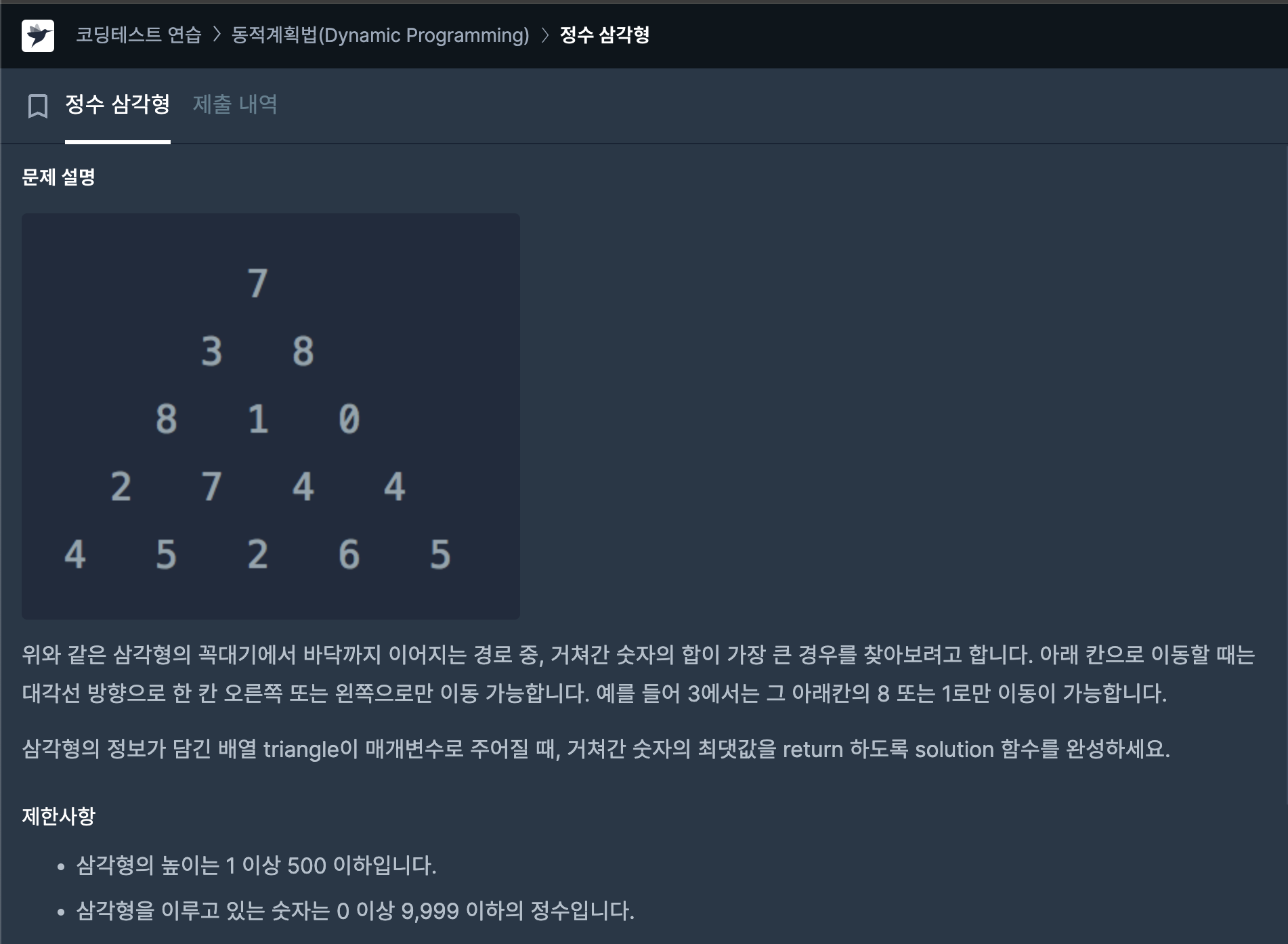
정수들로 이루어진 삼각형이 있다.

맨 위 꼭짓점에서 아래로 내려가는 중
거쳐가는 경로의 정수들의 합이 가장 큰 경우를 찾으려고 하는 문제이다.

이때 아래로 내려가는 방법에는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동이 가능하다.

입출력은 다음과같이 2차원 배열로 삼각형을 이루는 정수들을 받고,
최댓값을 return 해주면 된다.

위 예시에서는
7-3-8-7-5 를 거친 합인 30이 답이다.

---

어떻게 풀 수 있을까?

이는 dp로 풀이가 가능한데 dp를

dp[i][j] = i번째 줄 j칸까지 내려오며 만들 수 있는 최대 합

으로 놓고 풀면 편하다.

이때 i가 위아래 이고, j가 좌우 이다.

위에서 아래로 내려오는 방법은 두가지 중 하나이니까 그 둘중 더 크게 오는 경로에다가 내려왔을때의 값을 더해주는식으로 dp 배열을 만들 수 있다.

단, 삼각형 가장 가장자리의 경우(왼쪽, 오른쪽 둘다)
내려올 수 있는 경로가 한가지이다. 그래서 이것을 예외처리 해주어 dp를 구현해주면 된다.

해답 및 풀이

def solution(triangle):
    n = len(triangle)

    # dp 테이블을 triangle과 같은 모양으로 만들어준다.
    dp = []

    for row in triangle:
        dp.append(row[:]) # triangle 의 요소를 복사(슬라이싱)하여 새로운 row로 만들어 dp배열에 넣어준다.

    for i in range(1,n):
        for j in range(i + 1):    
            if j == 0: # 왼쪽 가장 자리
                dp[i][j] = dp[i-1][j] + triangle[i][j]
            
            elif j == i: #오른쪽 가장 자리
                dp[i][j] = dp[i-1][j-1] + triangle[i][j]
            
            else:
                dp[i][j] = max(dp[i-1][j-1], dp[i-1][j]) + triangle[i][j]

    return max(dp[-1])