
https://school.programmers.co.kr/learn/courses/30/lessons/1843
문제 파악
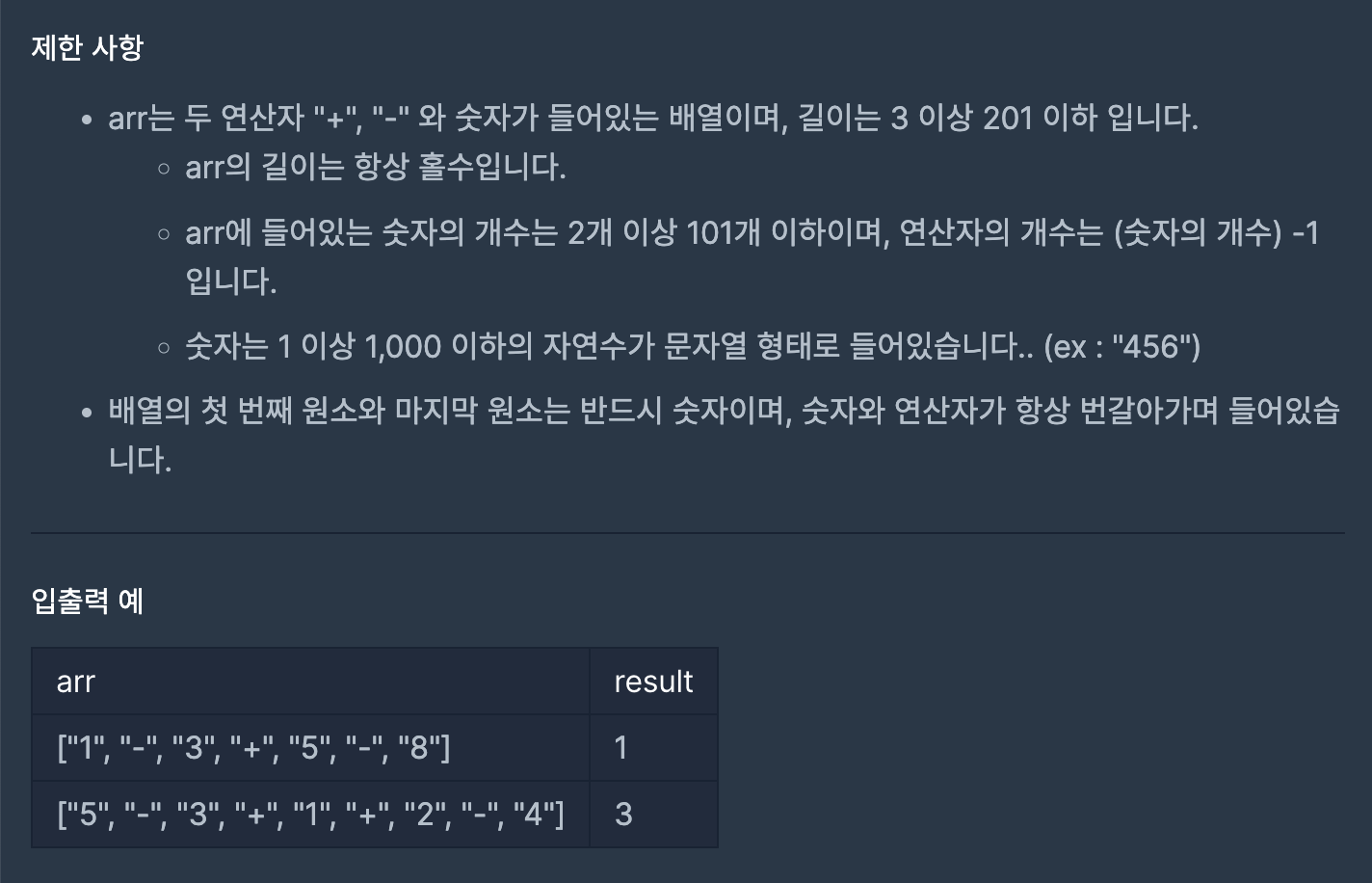
입력값으로 문자열 형태의 숫자와 사칙연산 기호들을 입력받는다.
이 문자열들을 순서바꿔가며 연산을 했을 때 나올 수 있는 결괏값들 중 최대값을 return해주면 된다.
인줄 알았는데 아니었다.
문자열들의 순서를 바꾸면 안되고,
순서는 그대론데 괄호만을 이용해서, 즉 연산 순서만 조작을 해주어서 최댓값을 도출해야 한다.
해결 아이디어 : DP
구간을 나누면서 최댓값/최솟값을 반복적으로 계산해야 하기 떄문에
같은 부분식을 여러번 쓰게 되니까 DP배열에 기억해둔다.
DP 배열 정의
max_dp[i][j]: i번째 수부터 j번째 수까지 계산했을 때 얻을 수 있는 최댓값
min_dp[i][j]: 같은 구간에서의 최솟값
왜 min_dp도 필요하냐면
뺄셈의 경우 최대-최소를 빼야 최댓값을 구할 수 있기 때문
초기값
구간 길이 1일 때는 그냥 자기 자신.
max_dp[i][i] = nums[i]
min_dp[i][i] = nums[i]
점화식
구간 [i..j]를 구하려면,
중간 k에서 나눠서
[i..j] = i..k [k+1..j]
op == '+':
max = left_max + right_max
min = left_min + right_min
op == '-':
max = left_max - right_min
min = left_min - right_max
구간 확장 방식
길이 1 구간은 초기화
길이 2, 3, … n 구간을 차례대로 계산
최종 답은 max_dp[0][n-1] 0부터 n-1까지의 최댓값
숫자가 n개면 인덱스는 0부터 n-1까지 있기 때문
해답 및 풀이
def solution(arr):
# 1) 숫자와 연산자 분리
nums = []
ops = []
for i in range(len(arr)):
if i % 2 == 0: # 짝수 인덱스 -> 숫자
nums.append(int(arr[i]))
else: # 홀수 인덱스 -> 연산자
ops.append(arr[i])
n = len(nums)
# 숫자가 하나라면 그대로 리턴
if n == 1:
return nums[0]
# 2) DP 테이블 준비
"""
max_dp[i][j]
i번째 숫자부터 j번째 숫자까지 계산했을 때 만들 수 있는 최댓값
min_dp[i][j]
i번째 숫자부터 j번째 숫자까지 계산했을 때 만들 수 있는 최솟값
nums = [1, 3, 5]라면
max_dp[0][2] = 1번째 숫자(1)부터 3번째 숫자(5)까지 계산했을 때의 최댓값
min_dp[0][2] = 같은 구간에서의 최솟값
"""
INF = 10 ** 15
max_dp = []
min_dp = []
for _ in range(n):
max_dp.append([-INF] * n) # 초기값은 아주 작은 수
min_dp.append([INF] * n) # 초기값은 아주 큰 수
# 3) 구간 길이가 1일때, 자기 자신이 최댓값이자 최솟값이다.
for i in range(n):
max_dp[i][i] = nums[i]
min_dp[i][i] = nums[i]
# 4) 구간 길이가 2 ~ n 일때
for length in range(2, n + 1): # 구간 길이: 2,3,...,n
for i in range(0, n - length + 1): # i = 시작 인덱스, j = 끝 인덱스
j = i + length - 1 # 예: i=0, length=3 → j=2 → [0..2]
# i~j 사이에서 구간을 나눌 분할점 k
for k in range(i,j):
op = ops[k]
left_max = max_dp[i][k]
left_min = min_dp[i][k]
right_max = max_dp[k+1][j]
right_min = min_dp[k+1][j]
if op == '+':
# 덧셈은 max끼리 더하면 최댓값, min끼리 더하면 최솟값
cand_max = left_max + right_max
cand_min = left_min + right_min
else: # op =='-': , 뺄셈은 대-소 = 최댓값, 소-대 = 최솟값
cand_max = left_max - right_min
cand_min = left_min - right_max
if cand_max > max_dp[i][j]:
max_dp[i][j] = cand_max
if cand_min < min_dp[i][j]:
min_dp[i][j] = cand_min
return max_dp[0][n-1] # 전체 구간 0~n-1 의 최댓값이 답 