조합논리회로
조합논리회로는 NOT, AND, OR의 세 가지 기본 논리회로의 조합으로 구성된 논리회로이며, 입력신호, 논리게이트, 출력신호로 구성됩니다.
2진 데이터를 입력받아서 원하는 2진 출력 데이터를 얻습니다.
가산기
가산기 adder는 조합논리회로에서 가장 기본적인 장치입니다.
반가산기
반가산기 half-adder는 한자리 2진수 2개를 입력받아 합 S와 캐리 C를 계산하는 조합논리회로입니다. 반가산기에서 캐리 C는 입력 A, B가 모두 1인 경우에만 1이되고 합 S는 입력 A, B 둘 중 하나만 1인 경우에 1이 됩니다.
다음은 반가산기의 진리표와 구조입니다.
| 입력 A | 입력 B | S | C |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
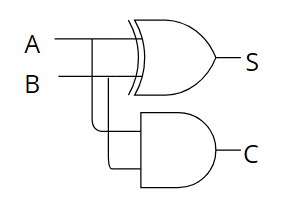
전가산기
반가산기는 2진수 한자릿수 덧셈을 수행하므로 아랫자리에서 올라온 캐리를 고려하여 계산할 수가 없습니다. 이러한 문제를 해결하고자 아랫자리의 캐리를 고려해 만든 조합논리회로가 전가산기 full-adder입니다.
전가산기는 입력 A, B 그리고 아랫자리에서 올라온 캐리 C-in을 포함한 한 자릿수 2진수 3개를 조합하는 회로입니다.
다음은 반가산기의 진리표와 구조입니다.
| 입력 A | 입력 B | C-in | S | C-out |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
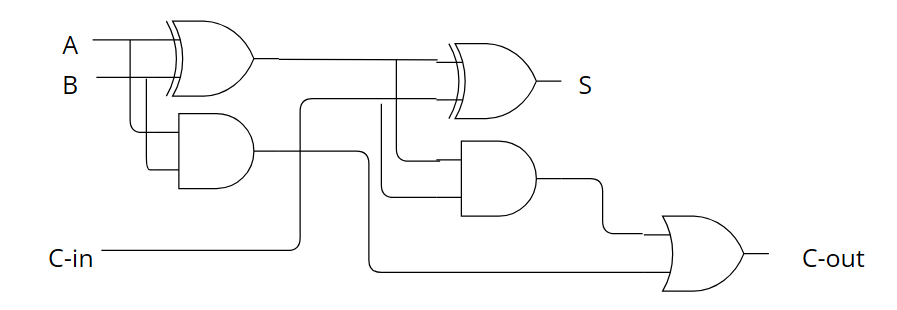 회로를 보면 알 수 있지만, 전가산기는 반가산지 2개와 OR 게이트 하나로 구성할 수 있습니다.
회로를 보면 알 수 있지만, 전가산기는 반가산지 2개와 OR 게이트 하나로 구성할 수 있습니다.
병렬가산기
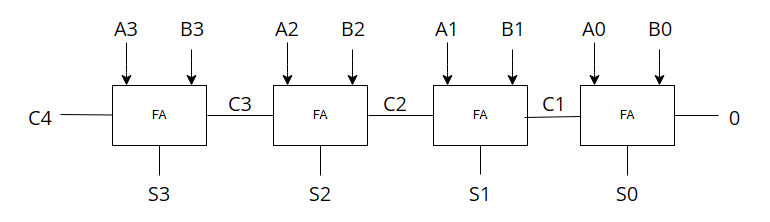
전가산기를 병렬로 연결하면 2비트 이상의 계산을 하는 가산기를 만들 수 있으며 이를 병렬가산기라고 합니다. 병렬 가산기에서 최하위 비트가 받는 캐리의 값은 0으로 고정합니다.
이때 병렬가산기의 입력 B들을 부호와 XOR 연산을 하여 입력으로 사용하면 덧셈과 뺄셈이 모두 가능한 병렬감가산기가 됩니다.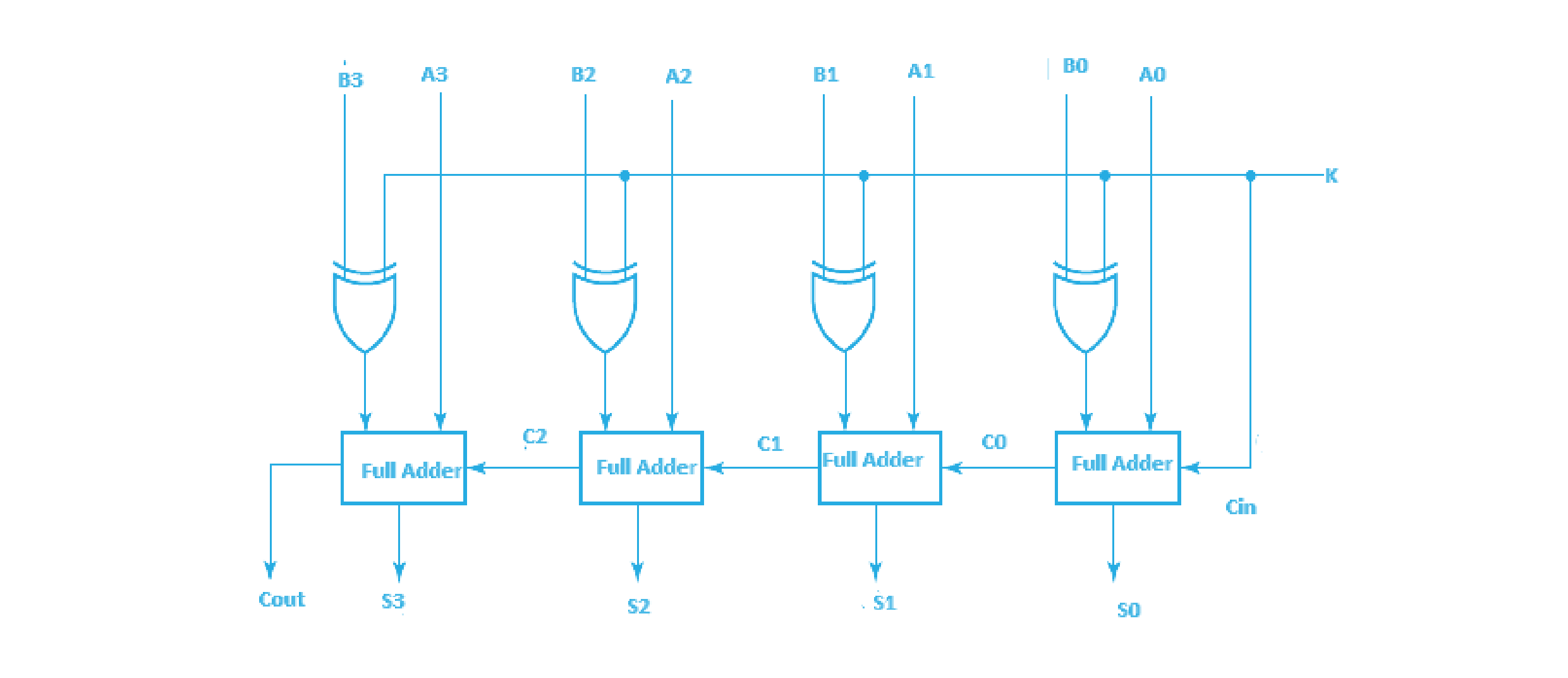
비교기
비교기 comparator는 두 2진수 값의 크기를 비교하는 회로입니다.
1비트 비교기
1비트 비교기의 회로와 진리표는 다음과 같습니다.
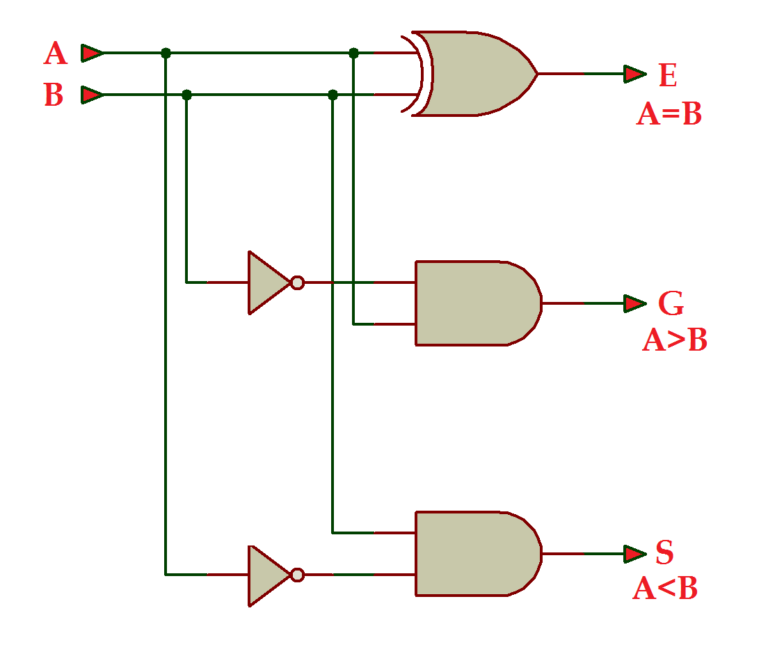
| 입력 A | 입력 B | 출력 E (A = B) | 출력 G (A > B) | 출력 S (A < B) |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 |
2비트 비교기
2비트 비교기의 회로와 진리표는 다음과 같습니다.
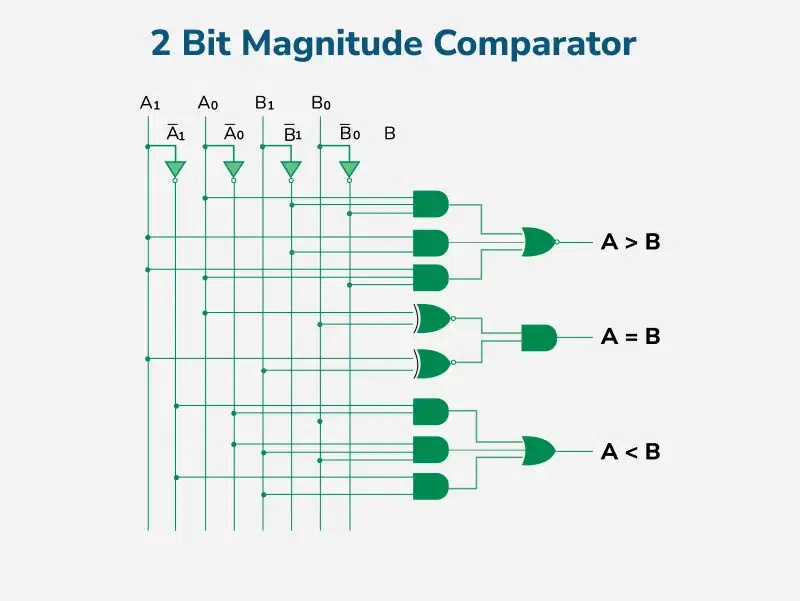
이미지 출처
https://www.geeksforgeeks.org/digital-logic/magnitude-comparator-in-digital-logic/
| A1 | A0 | B1 | B0 | A<B | A=B | A>B |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 |

