10진수
10진수(decimal number)는 우리가 일상에서 사용하는 숫자 체계입니다. 0에서 9까지 10개의 숫자를 사용해서 수를 표시합니다. 정수의 각 자릿수는 10의 거듭제곱으로 나타내고, 소수점은 10의 음의 거듭제곱의 형태로 나타냅니다.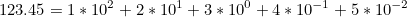
2진수
2진수(bunary number)는 주로 컴퓨터공학과 전자공학 분야에서 사용되는 체계로 0과 1의 두 가지 숫자로 수를 표현합니다.
초기에는 천공 카드를 이용해서 컴퓨팅을 했는데 구멍이 뚫리면 1 아니면 0과 같은 방식으로 사용했습니다. 그리고 반도체가 개발되면서 전류의 유무에 따라 1, 0을 표현하게 되었습니다.
10진수와 마찬가지로 2의 거듭제곱을 통해 정수부와 소수부를 표시합니다.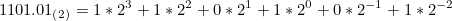
8진수
8진수(octal number)는 0~7까지의 숫자를 이용해 표기합니다. 2진수로 나타내면 정보가 너무 길어지기 때문에 이를 줄이고자 8진수와 후에 언급할 16진수를 사용하는 경우가 있습니다.
마찬가지로 8의 거듭제곱을 통해 정수부와 소수부를 표시합니다.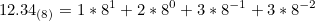
16진수
16진수(hexadecimal number)는 0~9까지의 숫자와 영어 A, B, C, D, E, F를 사용해 총 16개의 문자로 숫자를 표기하는 방식입니다. 8진수보다 더욱 축약시킬 수 있어서 어셈블리 레벨에서 자주 사용되는 체계입니다.
16진수의 영문자들의 경우 각각 10진수로
A는 10,B는 11,C는 12,D는 13,E는 14,F는 15에 대응됩니다.
역시 10의 거듭제곱을 통해 정수부와 소수부를 표시합니다.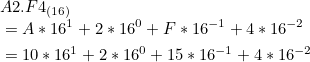
진법 변환
대표적으로 사용되는 4가지 진법들에 대해 알아보았으니, 이번엔 각 진법간 변환 방법을 알아보겠습니다.
2진수 -> 10진수
2진수에서 10진수 변환은 각 자릿수에 대해 2의 거듭제곱을 계산합니다.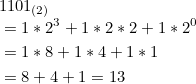
2진수-8진수, 2진수-16진수
2진수-8진수, 2진수-16진수간의 변환은 정말 간단합니다.
-
2진수 -> 8진수
아주 간단합니다. 소수점을 기준으로 2진수를 세 자리씩 끊은 후 끊은 수를 8진수로 바꾸면 됩니다.1101010100은1 101 010 100로 끊어집니다. 그리고 각 자릿수를 계산하면1 5 2 4라는 8진수로 간단하게 변환이 가능합니다. -
8진수 -> 2진수
이 경우는 각 자릿수를 3자리의 이진수로 변환하면 됩니다.436이라는 8진수가 있다고 가정하면,4 3 6을 3자리 이진수로 바꿔줍니다.
따라서100 011 110이라는 2진수로 변환이 됩니다. -
2진수 -> 16진수
8진수와 원리가 같습니다. 다만 이번에는 4자리씩 끊어서 변환합니다. 위에서 언급했듯이 10이면 A, 11이면 B, ...로 변환합니다.1101010100은11 0101 0100로 끊어집니다. 따라서3 5 4라는 16진수로 변환이 됩니다. -
16진수 -> 2진수
마찬가지로 각 자리를 4자리의 2진수로 변환합니다.A3B는1010 0011 1011로 변환됩니다.
10진수 변환
10진수 -> 2진수
10진수에서 2진수 변환은 정수부와 소수부일 경우가 다릅니다.
먼저 정수부분의 변환은 10진수를 2로 나눕니다. 이때 나온 나머지가 2진수의 앞부분에 붙습니다.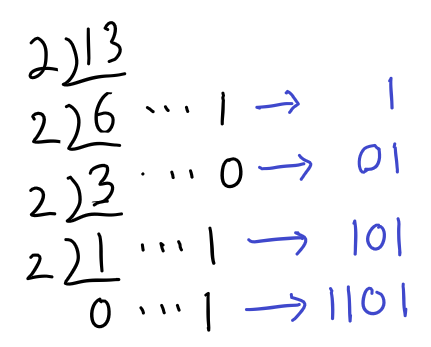
반대로 소수부분은 소수부에 2를 곱합니다. 그러면 정수 1의 자리가 1또는 0이 되는데, 이 일의 자리를 소숫점의 뒤에 붙여줍니다. 이때 연산은 소수부가 0이 될 때 까지 반복해서 수행합니다.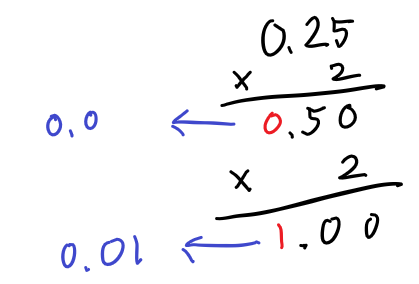
소수부분의 변환의 경우 대부분의 경우에서 무한대로 반복하여 나타나는 경우가 있습니다. 이 경우에 특정 자릿수에 끊게 되는데 이런 이유로 인해서 몇몇 연산의 경우 오차가 발생합니다.
10진수 -> 8진수
역시 동일한 방식으로 진행합니다.
정수부는 8로 나눈 나머지를 채우고, 소수부는 8을 곱한 일의 자리를 채워넣습니다.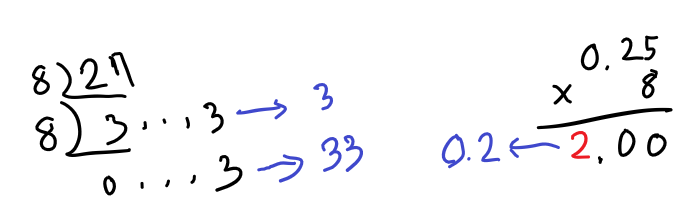
10진수 -> 16진수
마찬가지로 정수부는 16을 나눈 나머지를 채우고, 소수부는 16을 곱한 일의 자리를 채웁니다.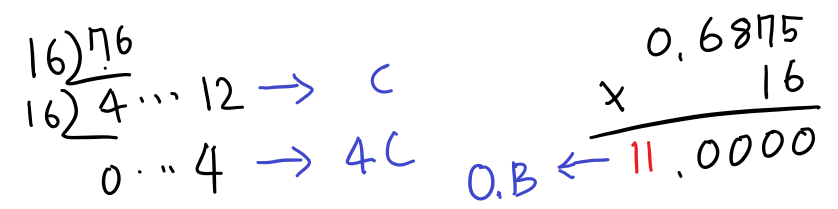
이렇게 디지털 시스템에서 사용되는 자주 사용되는 숫자 체계인 2, 8, 10, 16진수와 그 변환법에 대해서 알아보았습니다.
개인적인 경험으로는 10진수에서 8 또는 16진수를 변환할 때는 8을 나누고 곱하고, 16을 나누고 곱하는 연산이 실수가 발생할 확률이 높았습니다.
그래서 10진수를 2진수로 바꾸고 3자리씩 끊어서 8진수로 변환하고, 4자리씩 끊어서 16진수로 변환하는 방식을 사용하여 좀 더 빠르고 정확하게 진법 변환을 수행할 수 있었습니다.

