컴퓨터에서 사용되는 몇 가지 코드들에 대해 알아보겠습니다.
BCD 코드
BCD 코드(Binary Coded Decimal)은 10진수 0~9를 2진화한 코드입니다. 표기는 2진수지만 실제 표기는 10진수 처럼 사용하게 됩니다. 이에 따라 10 이상의 수를 의미하는 1010 ~ 1111은 사용하지 않습니다.
말로 하면 어렵지만 각 자릿수를 0 ~ 9의 2진수로 나타낸다고 생각하면 쉽습니다.
| 10진수 | BCD 코드 | 10진수 | BCD 코드 |
|---|---|---|---|
| 0 | 0000 | 10 | 0001 0000 |
| 1 | 0001 | 11 | 0001 0001 |
| 2 | 0010 | 21 | 0010 0001 |
| 3 | 0011 | 31 | 0011 0001 |
| 4 | 0100 | 41 | 0100 0001 |
| 5 | 0101 | 99 | 1001 1001 |
| 6 | 0110 | 100 | 0001 0000 0000 |
| 7 | 0111 | 101 | 0001 0000 0001 |
| 8 | 1000 | 111 | 0001 0001 0001 |
| 9 | 1001 | 777 | 0111 0111 0111 |
BCD 코드의 연산
BCD 코드의 연산은 10진수 처럼 수행합니다.
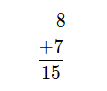
위와 같은 10진수 연산을 BCD 코드 연산으로 나타내면 다음과 같습니다.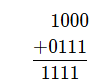
이때 1111이라는 결과처럼 BCD 코드에서 사용되는 수의 범위를 넘어서게 되면, 계산 결과에 6 (0110 BCD)를 더해줍니다.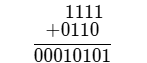
결과가 BCD 코드 0001 0101 즉, 15로 나오게 됩니다.
3초과 코드
3초과 코드 (excess-3 code)는 BCD 코드에 3(0011)을 더한 코드입니다.
| 10진수 | BCD 코드 | 3초과 코드 |
|---|---|---|
| 0 | 0000 | 0011 |
| 1 | 0001 | 0100 |
| 2 | 0010 | 0101 |
| 9 | 1001 | 1100 |
이 코드는 자기 보수의 성격을 가집니다.
보수 補數, Complement는 다음과 같습니다.
현재값 x에 대해 n의 보수라고 표현하게 되는 경우,n - x의 값을 x에 대한 n의 보수라고 합니다.예를들어 10진수에서 3에 대한 5의 보수는 2가 됩니다.
3초과 코드의 자기 보수 성격은 어떤 수에 대해 9의 보수를 취하면 그 결과가 유효한 3초과 코드가 된다라는 것을 의미합니다.
예를들면 10진수 2의 3초과 코드는
0101, 7은1010인데 이들은 서로 비트 반전(서로 유효한 3초과 코드이자 9의 보수) 효과를 가지게 됩니다. 즉, 비트 반전으로 9의 보수를 쉽게 찾을 수 있다는 특징이 있습니다.
또한 0000, 0001, 0010, 1101, 1110, 1111은 3초과 코드에서 등장하지 않으므로 오류 검출시에 이들이 검출되면 오류가 발생했다는 것을 알 수 있게 됩니다.
그레이 코드
그레이 코드 (gray code)는 입출력 장치나 아날로그-디지털 변환에 사용되는 코드입니다. 그레이 코드는 연속된 코드들 간에 하나의 비트만 변하여 다음 코드가 됩니다. 그렇기 때문에 입력 시에 그레이 코드를 사용하면 오차가 적어진다는 특징을 갖습니다.
| 10진 코드 | 2진 코드 | 그레이 코드 |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 11 | 1011 | 1110 |
2진 코드 <-> 그레이 코드 변환
다음과 같은 과정으로 2진 코드를 그레이 코드로 변환합니다.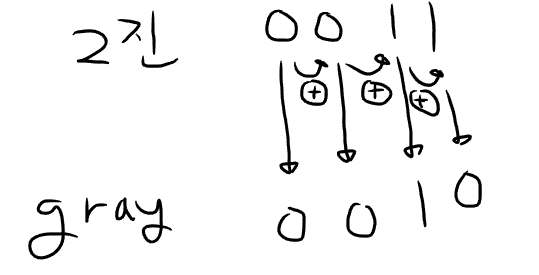
- 최상위 비트는 그대로 쓴다. (위 그림에선 4비트 2진 코드이므로 제일 왼쪽 비트)
- 그 다음 자리 코드와 비교해서
같으면 0, 다르면 1을 쓴다. (XOR 연산)
반대로 그레이 코드를 2진 코드로 변경하는 법은 다음과 같습니다.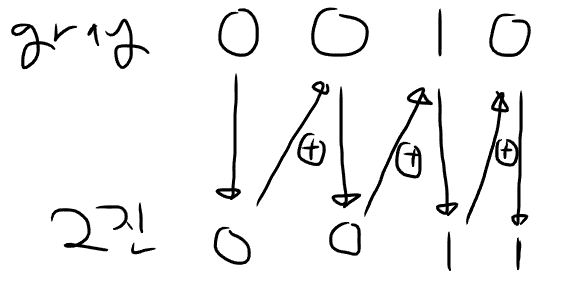
- 최상위 비트는 그대로 쓴다.
- 생성된 2진 비트와 그 다음 자릿수의 그레이 코드를 비교하여
같으면 0, 다르면 1을 쓴다. (XOR 연산)
패리티 비트
주기억장치에서 사용되는 가장 간단한 에러 검출 코드로는 패리티 비트 (parity bit)를 사용합니다.
패리티 비트는 데이터 내에서 1의 개수를 짝수로 맞춰주는 짝수 패리티와 홀수로 맞춰주는 홀수 패리티가 존재합니다. 따라서 데이터 전송 후 에러 검출 시 1의 개수가 짝수 개이고 짝수 패리티이거나 홀수 개이고 홀수 패리티라면 데이터가 이상 없이 정확하게 전송된 것입니다. 만약 패리티와 1의 홀짝이 맞지 않는다면 데이터 전송과정에서 에러가 발생된 것을 확인할 수 있게됩니다.
패리티 비트를 하나만 사용하는 경우에는 에러를 검출할 수 있지만 정정할 수는 없습니다. 따라서 에러 검출 및 정정을 위해서는 병렬 패리티라는 개념을 사용합니다.
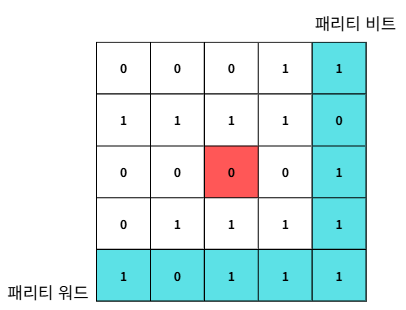위 표와 같이 가로와 세로에 대해 패리티 비트를 만들고 블록 단위로 전송합니다. 이때 블록의 패리티 비트, 워드를 검사해서 틀린 부분이 있다면 그 교차 지점(붉은색)에서 에러가 발생했다고 검출 및 정정이 가능해집니다.
ASCII 코드
ASCII 코드 (American Standard Code for Information Interchange)는 3비트의 zone과 4비트의 digit에 1비트의 패리티 코드를 추가한 8비트짜리 코드이며 영어 대소문자, 특수문자, 숫자, 제어문자 등을 나타냅니다.
아스키 코드는 총 128가지 문자를 표현이 가능하며 확장된 아스키 코드를 통해 최대 255개의 추가 문자를 제공하고 있습니다.
https://www.ascii-code.com/
위 링크에서 0~127개의 기본 아스키 코드 및 확장된 아스키 코드를 확인하실 수 있습니다.
유니코드
영어권만 표현할 수 있는 아스키 코드나 기타 언어/기호들을 표현하기 위해 다른 기호화 시스템을 추가적으로 사용해야하는 불편함을 덜기 위해 유니코드 unicode가 개발되었습니다.
유니코드는 아스키 코드의 한계성을 극복한 인터넷의 표준 코드입니다. 각 언어의 문자 표현을 위해 고유한 코드 포인트를 부여하여 U+XXXX의 형태로 언어를 나타내게 됩니다. (예: U+0041 = 'A', U+AC00 = '가', 이때 X는 16진수 U+0000 ~ U+FFFF)
이런 유니코드를 실제로 저장하거나 전송하기 위해서는 인코딩을 수행해야합니다. 대표적인 유니코드 인코딩은 다음과 같습니다.
- UTF-8: 가변 길이 1 ~ 4바이트 인코딩, 아스 코드 호환, 인터넷 표준
- UTF-16: 2바이트 or 4바이트, Windows OS/Java 내부 문자열 표현에서 사용
- UTF-32: 고정 길이 4바이트. 단순하게 표현되나 메모리 사용량이 많아 비효율적
가 → 코드 포인트: U+AC00
- UTF-8: EA B0 80 (3바이트)
- UTF-16: AC00 (2바이트)
- UTF-32: 0000AC00 (4바이트)
