논리 게이트
논리 게이트는 하나 이상의 입력 단자와 하나의 출력 단자로 구성되는 전자 회로이며, 논리 게이트들이 모여 하나의 논리회로를 구성하게 됩니다.
디지털 시스템에서는 흐르는 전압의 양을 1과 0의 두 가지 구분된 값으로 인식하게 됩니다. 이에따라 논리 게이트는 1과 0 두 가지 신호를 발생시키는 기능을 합니다.
논리 게이트는 기본적으로 스위치의 역할을 하는 트랜지스터로 구성되어 있습니다.
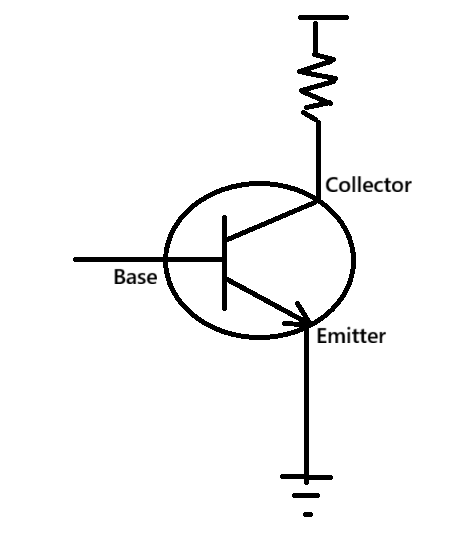베이스의 입력 전압이 임계값보다 작으면 높은 저항 상태가 되고 입력된 전압이 출력에 나타나게 됩니다. 이 값이 논리 1에 해당하는 전압값이면 전기 신호를 1로 나타내게 됩니다. 반면 입력 전압이 임계값보다 크면 컬렉터와 에미터가 연결되고 출력은 0이 됩니다. (논리 부정 NOT으로 동작)
디지털 시스템(컴퓨터 포함)들은 여러 논리게이트가 모여 조합논리회로, 순서논리회로로 구성되며 각 게이트는 서로 다른 그림으로 표현됩니다.
논리게이트 조합에서 NOT, AND, OR은 기본이 되는 논리게이트이고, 기본 논리게이트들을 조합하여 다른 게이트를 만드는데 이들 종류에는 NAND, NOR, XOR, XNOR 게이트 등이 있습니다.
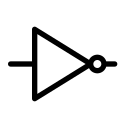
NOT 게이트
NOT 게이트 는 입력 하나와 출력 하나로 구성된 게이트이며 논리 부정을 의미합니다. 논리 부정에 의해 입력의 반대로 출력됩니다.
NOT 게이트의 입력/출력 값 및 기호는 다음과 같습니다.
| 입력 A | 출력 F |
|---|---|
| 0 | 1 |
| 1 | 0 |
버퍼 게이트
버퍼 게이트는 입력된 신호를 그대로 출력하는 게이트입니다.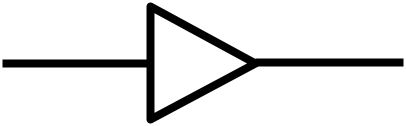
| 입력 A | 출력 F |
|---|---|
| 0 | 0 |
| 1 | 1 |
논리식: A'
3상태 버퍼 게이트는 출력이 3개의 값 중 하나(Low 0, High 1, 하이 임피던스) 중 하나의 값을 갖는 논리 게이트입니다.
버퍼에 제어단자 E를 추가했으며, E는 입력과 출력 사이의 회로 개폐 상태(Low or High)를 제어하는 역할을 합니다.
- 제어단자가 Low인 경우
| 입력 A | 제어단자 E | 출력 F |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 하이 임피던스 |
| 1 | 1 | 하이 임피던스 |
- 제어단자가 High인 경우
| 입력 A | 제어단자 E | 출력 F |
|---|---|---|
| 0 | 0 | 하이 임피던스 |
| 1 | 0 | 하이 임피던스 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
AND 게이트
AND 게이트는 2개 이상의 입력에 대해 1개의 출력을 얻는 게이트이며 논리곱을 의미합니다.
AND 게이트는 입력이 모두 1인 경우에만 출력이 1이되고, 입력에 하나라도 0이 있다면 출력이 0이 됩니다.
다음은 입력이 2개인 AND 게이트에 대한 기호와 출력 값입니다.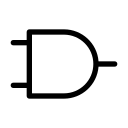
| 입력 A | 입력 B | 출력 F |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
논리식: F = AB
OR 게이트
OR 게이트는 2개 이상의 입력에 대해 1개의 출력을 얻는 게이트이며 논리합을 의미합니다.
OR 게이트는 입력이 모두 0인 경우에만 출력이 0이되고, 입력에 하나라도 1이 있다면 출력이 1이 됩니다.
다음은 입력이 2개인 OR 게이트에 대한 기호와 출력 값입니다.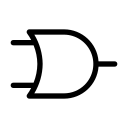
| 입력 A | 입력 B | 출력 F |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
논리식: F = A + B
NAND 게이트
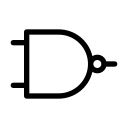
NAND 게이트는 2개 이상의 입력에 대해 1개의 출력을 얻는 게이트입니다. 동작은 AND 게이트의 부정 (NOT-AND)으로 입력이 모두 1인 경우에만 출력이 0이 되고, 그렇지 않은경우 출력이 1이 됩니다.
| 입력 A | 입력 B | 출력 F |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
논리식: F = (AB)'
NOR 게이트
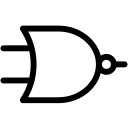
NOR 게이트는 2개 이상의 입력에 대해 1개의 출력을 얻는 게이트입니다. 동작은 OR 게이트의 부정 (NOT-OR)으로 입력이 모두 0인 경우에만 출력이 1이 되고, 그렇지 않은경우 출력이 0이 됩니다.
| 입력 A | 입력 B | 출력 F |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
논리식: F = (A + B)'
XOR 게이트
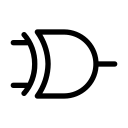
XOR 게이트(eXclusive OR)는 2개 이상의 입력에 대해 1개의 출력은 얻는 게이트입니다. XOR 게이트는 1이 홀수 개만큼 입력되면 1을 출력하고, 짝수 개만큼 입력되면 0을 출력합니다.
| 입력 A | 입력 B | 출력 F |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
논리식: F = AB' + A'B
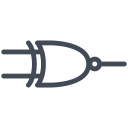
XNOR 게이트
XNOR 게이트(eXclusive NOT-OR)는 2개 이상의 입력에 대해 1개의 출력을 얻는 게이트입니다. XNOR 게이트는 짝수 개의 1이 입력되면 1을 출력하고, 홀수 개만큼 입력되면 0을 출력합니다.
| 입력 A | 입력 B | 출력 F |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
논리식: F = A'B' + AB
정논리, 부논리
지금까지의 게이트에 대한 설명은 High에서 1, Low에서 0 논리를 의미했습니다. 이러한 개념을 정논리 positive logic이라고 합니다. 반대로 High에서 0, Low에서 1을 의미하는 논리 개념을 부논리 negative logic이라고 합니다.
정논리와 부논리의 이러한 관계에 따라 정논리의 입력과 출력에 NOT 개념을 추가하면 부논리로 변환됩니다.
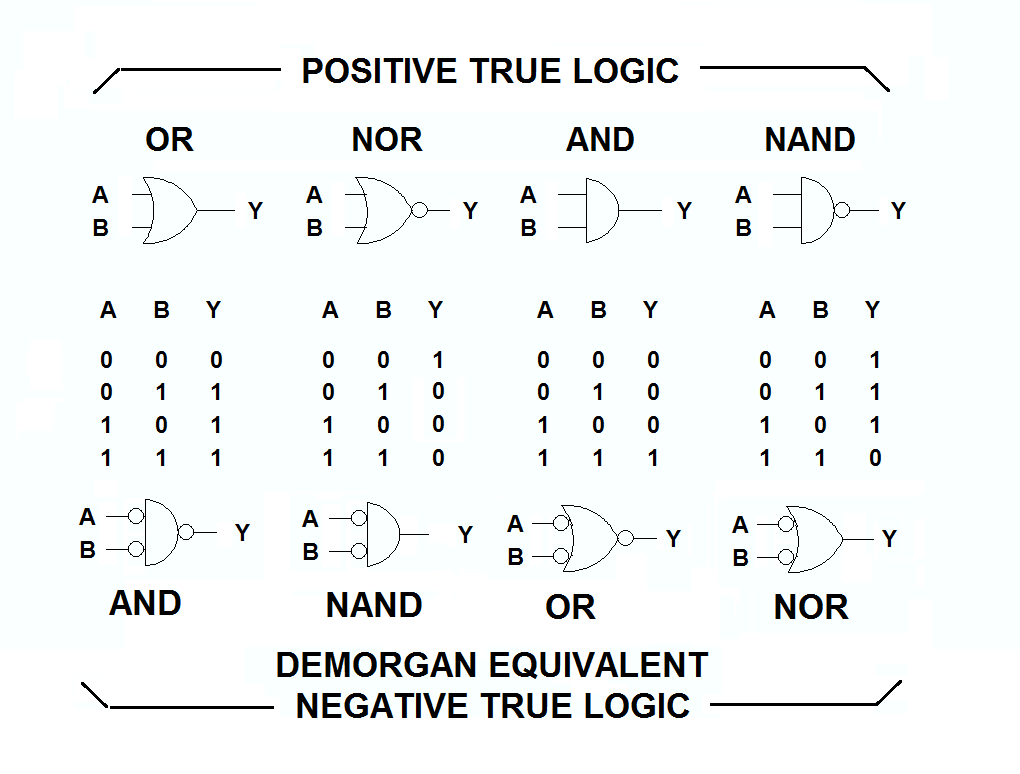
이미지 출처: https://electronics.stackexchange.com/questions/53019/negative-logic-and-positive-logic-gates
