불 대수
불 대수(Boolean Algebra)는 논리식을 간소화하여 표현하기 위한 수학 개념입니다.
불 대수는 NOT, AND, OR 연산을 이용하고, 각 입력과 출력에는 알파벳을 사용합니다. 이때
NOT은 ' 또는 윗줄, AND는 곱셈, OR는 덧셈을 이용하여 표현합니다.
불 대수 법칙
불 대수 공리
AND, OR 연산에 적용되는 공리는 다음과 같습니다.
- P1:
A = 0orA = 1 - P2:
0 * 0 = 0 - P3:
1 * 1 = 1 - P4:
0 + 0 = 0 - P5:
1 + 1 = 0 - P6:
1 * 0 = 0 * 1 = 0 - P7:
1 + 0 = 0 + 1 = 1
불 대수 기본 법칙
위에서 소개한 공리를 바탕으로 나타내는 불 대수의 기본 법칙은 다음과 같습니다.
| 종류 | 불 대수식 |
|---|---|
| 기본 | A+0=0+A=A A+1=1+A=1 A+A=A A·0=0·A=0 A·1=1·A=A A·A=A A+A′=1 A·A′=0 A″=A |
| 교환 | A+B=B+A A·B=B·A |
| 결합 | A+(B+C)=(A+B)+C A·(B·C)=(A·B)·C |
| 분배 | A·(B+C)=A·B+A·C A+(B·C)=(A+B)(A+C) |
| 흡수 | A+(A·B)=A A·(A+B)=A A+(A′·B)=A+B |
| 드모르간 | (A+B)′=A′·B′ (A·B)′=A′+B′ |
논리회로의 논리식 변환
이제 불 대수의 공리 및 법칙들을 알아봤으니 간단한 논리회로를 가지고 논리회로를 논리식으로 변환하는 방법에 대해서 알아보도록 하겠습니다.
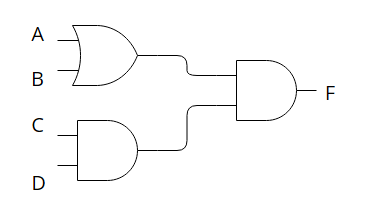위와 같은 논리회로에서 출력 F를 의미하는 불 대수 논리식을 도출해보겠습니다.
입력 A, B, C, D부분부터 시작합니다.
- A와 B는
OR 게이트 (논리합)으로 입력되므로A + B - C와 D는
AND 게이트 (논리곱)으로 입력되므로CD - 이후
A + B,CD가AND 게이트로 입력되므로(A + B)CD
따라서 위 회로의 논리식은 F = (A + B)CD가 됩니다.
논리식의 논리회로 변환
반대로 논리식의 논리회로 변환도 가능합니다. 논리회로의 논리식 변환을 반대로 수행하면 됩니다.
- 논리식의 항을
(A + B)와 CD로 나눈다. 이들은 논리곱으로 연결되어 있으니 최종 게이트에AND 게이트를 그립니다. - 이후 분리된 각 항의 입력과 게이트를 분석하여 회로를 구성해나갑니다.
불 대수식의 표현
불 대수식은 곱의 합 (SOP, Sum Of Product, AND-OR 결합)과 합의 곱(POS, Product Of Sum, OR-AND 결합) 두 가지 기본 형태로 표현됩니다.
곱의 합과 최소항
곱의 합은 입력의 1단계가 AND 항(곱의 항)으로 구성되고 출력인 2단계가 OR 항(합의 항)으로 이루어진 논리식입니다. 즉, 각 항은 모두 AND로 구성되고 구성된 항들을 OR 항으로 결합한 것들을 곱의 합이라고 합니다. (ex. F = AB' + ABC + CD, F = AC + B, F = A 등)
동일한 결과를 하는 논리식을 다양한 형태의 곱의 합으로 나타낼 수 있습니다. 이때 여러 SOP들 중에서 최소 곱들의 항들로 이루어진 식을 최소항라고 합니다.
합의 곱과 최대항
합의 곱은 입력의 1단계가 OR 항(합의 항)으로 구성되고 출력인 2단계가 AND 항(곱의 항)으로 이러진 논리식입니다. 즉, 각 항은 모두 OR로 구성되고 구성된 항들을 AND 항으로 결합한 것들을 합의 곱이라고 합니다. (ex. F = (A + B)(A + C), F = A + B, F = A 등)
모든 입력 변수를 포함하는 OR 항을 최대항이라고 합니다.
최소항과 최대항
앞에서 본 개념에 따르면 최소항은 특정 식에서만 출력이 1인 항을 SOP로, 최대항은 특정 식에서만 출력이 0인 항을 POS로 나타낸 것이기 때문에 최소항과 최대항은 서로 보수 관계에 있다고 할 수 있습니다.
