[논문 리뷰] Scalable and Equitable Math Problem Solving Strategy Prediction in Big Educational Data

논문: https://arxiv.org/abs/2308.03892

학생의 문제 해결 전략을 이해하는 것은 지능형 튜터링 시스템(Intelligent Tutoring Systems, ITS) 및 적응형 교육 시스템(Adaptive Instructional Systems, AIS)을 통한 효과적인 수학 학습에 큰 영향을 미칠 수 있다.

문제 해결에 사용된 전략은 학생의 숙련도를 나타낼 수 있다. 또한, 잘못된 전략에서 드러나는 특정 오개념을 바로잡기 위한 개인화 학습을 제공하고, 전략을 개선하기 위한 특정 문제를 설계하며, 학생의 사고 방식을 반영한 지도로 학생의 좌절감을 최소화할 수 있다.

PURPOSE

수학 학습에 있어서 확장 가능하고 공정한
학생의 문제 풀이 전략 예측 모델을 개발하는 것이 논문의 목표이다.

• 확장 가능성:
  전체 데이터의 일부만을 샘플링하더라도 효율적인 학습 가능한 것.

• 공정성:
  (숙련도나 기술 수준에 차이가 존재하는) 학습자 유형에 따라 모델 정확도가 다르지 않은 것.

DATASET

미국 수학 교육 플랫폼인 MATHia를 활용한 실제 학생들의 학습 데이터를 사용했다.

• 학생과 컴퓨터 간의 상호작용 및 학생의 문제 해결 행동에 대한 로그를 포함한 것이다.
  (예: 사용된 지식 구성 요소(Knowledge Component), 해당 단계(KC)가 올바르게 완료되었는지 여부, 힌트가 필요한지 여부 등)

• PSLC datashop을 통해 공개적으로 이용 가능하다고 논문에 적혀 있었으나, 실제 데이터셋을 다운받아 확인해보기 어려웠다.
  Bridge to Algebra 2008-2009 (BA08),
  Carnegie Learning MATHia 2019-2020 (CL19).

• 연립방정식 문제를 해결하는 3가지 전략으로,
  유사한 색상은 유사한 단계(KC)를 나타내며, 여러 전략들은 완전히 동일하지 않더라도 유사하거나 대칭적인 경우가 많다.

3. PROPOSED APPROACH

학생 $𝑆$와 문제 $𝑃$에 대해,
$𝑆$가 $𝑃$를 해결하는데 사용할 전략(KC 시퀀스)을 예측하는 것이
논문에서 해결하고자하는 과제이다.

3.1 MVec Embeddings

Node2Vec와 유사한 접근법을 활용하되, KC $K$에 대한 학생 $S$의 숙련도(Mastery)를 이용해 그래프에서 경로를 샘플링하여 임베딩을 학습하는 것이다.

숙련도 값은 Attention 모델을 활용해 각 KC가 문제 해결에서 차지하는 역할(중요도)를 포함하여 계산한다.

관계 그래프 $G=(V,E)$의 구성

• 훈련 데이터의 각 학생과 문제, KC를 노드 $V∈V$로 표현한다.

• 학생 $S$가 문제 $P$를 해결하는 데 KC $K$를 사용하는 경우, 두 개의 간선 $E,E′∈E$가 생성된다.

  • $E$: 학생 노드와 KC 노드를 연결.
  • $E′$: KC 노드와 문제 노드를 연결.

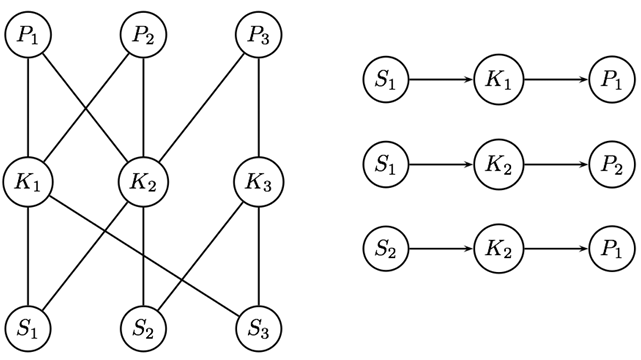
• 좌측 그래프는 3명의 학생, 문제, 그리고 KC에 대한 예시 그래프이며,
  우측은 임베딩을 학습하기 위해, 그래프에서 경로를 샘플링한 결과이다.

• 간단한 샘플링 전략 $Q$는 노드의 이웃을 무작위로 샘플링하는 것이지만,
  학생이 KC를 문제에 성공적으로 적용했다면, 해당 간선은 더 큰 중요도를 부여받아야 한다. 따라서 Attention 모델을 훈련하여 그래프 $G$의 간선에 대한 샘플링 확률을 추정한다.

숙련도(CFA) 정량화

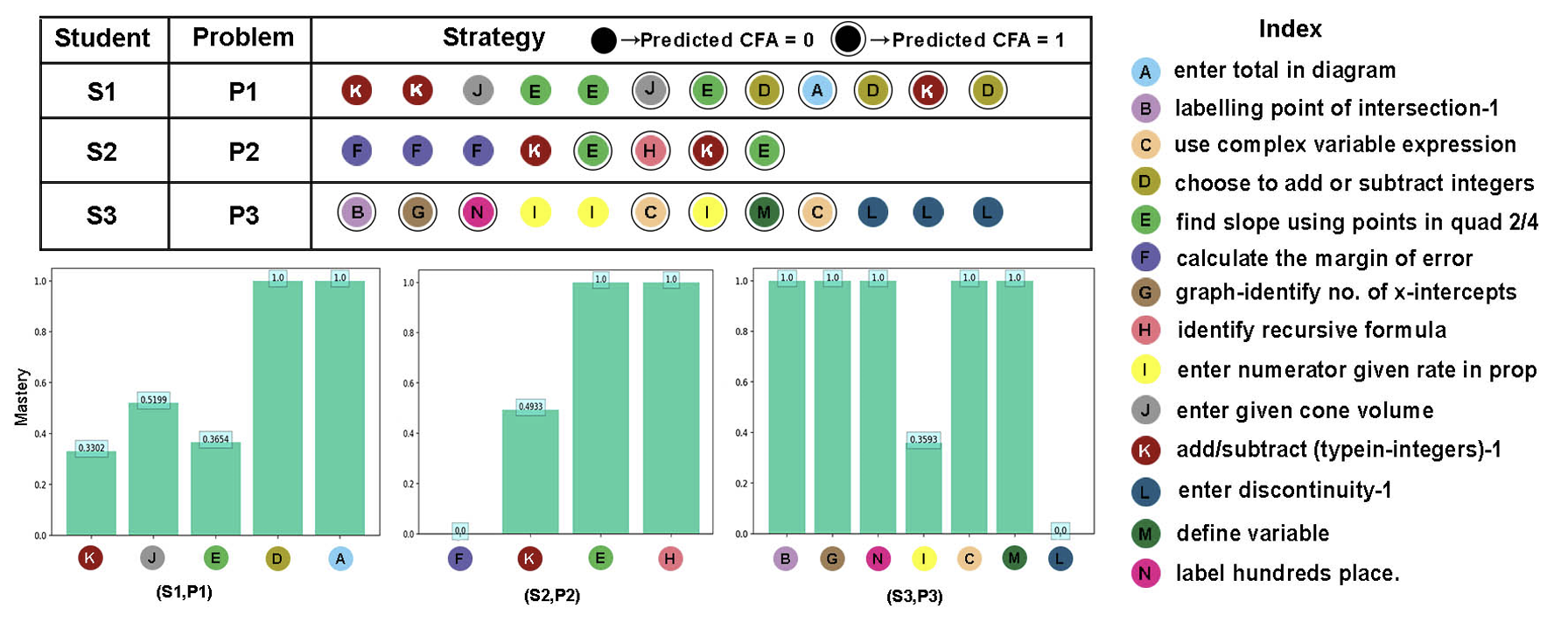
• 세 학생이 각 문제에 대해 KCs를 적용할 기회를 갖는 모습을 설명한다.

• CFA(Correct First Attempt)

  • 각 KC 시퀀스에 대해, 학생이 해당 KC를 적용할 기회를 가졌을 때 첫 번째 시도에서 올바르게 해결했는지(Correct, 1) 또는 잘못했는지(Wrong, 0)를 예측하는 값이다.
  • 1번 학생은 동일한 KC을 적용하는데 있어 일관성이 부족하다.
    (앞선 두번의 KC K는 올바르게 해결하지 못하였지만, 뒤에서는 올바르게 해결한 모습 등으로 CFA 값이 0과 1 사이의 값을 가짐)
    반면, 2, 3번 학생은 동일한 KC를 일관되게 적용하므로, 숙련도가 높다고 볼 수 있다.

• 교육과정 구조(단원 → 차시)를 기반으로 Attention 모델을 학습시켰다.

• 각 차시에서 학생이 해결한 문제 $P$를 선택하고,
  $P$에서 사용된 각 KC에 대한 CFA 값을 예측하도록 모델을 훈련했다

• (CFA 값 예측을 위한) Attention 모델 구조

  • 인코더-디코더(encoder-decoder) 구조로, 입력은 KC 시퀀스로 구성되며, 인코더는 이 시퀀스를 잠재 표현으로 매핑하고 디코더는 CFA 값을 하나씩 디코딩한다.

  • Attention 가중치 계산:

    $\text{Attention}(\gamma, \kappa, \eta) = \text{softmax}\left(\frac{\gamma \kappa^T}{\sqrt{d_k}} \eta\right)$
    • $γ, κ, η$: 각각 쿼리(query), 키(key), 값(value) 행렬.
    • $d_k$​: 잠재 표현의 차원.
    • 각 KC가 문제 해결에서 차지하는 역할(중요도)을 나타낸다고 볼 수 있다.

  • KC $K$에 대한 학생 $S$와 문제 $P$의 숙련도(CFA) 투영 계산:

    $\alpha(S, P, K) = \frac{\sum_{v \in \pi(a_i)} v}{\sum_{v \in \pi(a_i)} v + \sum_{v' \in \bar{\pi}(a_i)} v'}$
    • $π(⋅)$: 입력 벡터에서 모델이 해당 단계를 올바르게 해결했다고 예측한 값만 추출.
    • $\bar{\pi}(\cdot)$: $π(⋅)$의 보완 집합으로, 학생이 해당 단계를 틀렸다고 예측한 값 추출.
    • $i$: $K$가 사용된 모든 인스턴스의 합산.

그래프 $G$에서 경로 샘플링

분리된 분포(아래의 식)를 사용해서 그래프 G에서 경로를 샘플링한다.

• $Q(S)$: 학생 노드를 샘플링할 확률.
  • 균등 분포로 가정 (즉, 모든 학생이 동일한 확률로 선택됨).

• $Q(K∣S)$: 학생 $S$에게 주어진 $K$(Knowledge Component)를 샘플링할 확률.

  $Q(K|S) = \frac{1}{n} \sum_p \alpha(S, P, K)$
  • $n$: 학생 $S$가 KC $K$를 적용할 기회.
  • $\alpha(S, P, K)$: 학생 $S$의 문제 $P$에 대한 KC $K$의 숙련도.

• $Q(P∣K,S)$: S와 K가 주어졌을 때 문제 P를 샘플링할 확률.
  

MVec 임베딩 학습

1. $Q(S)$에서 무작위로 학생 $S$ 샘플링.
2. $Q(K∣S)$에서 $K$를 샘플링.
3. $Q(P∣K,S)$에서 $P$를 샘플링.
4. Word2Vec 모델을 통해 이웃 노드를 사용하여, 경로의 각 노드 예측.
5. Word2Vec 모델의 은닉 계층에서 임베딩 학습.

---

3.2 Non-Parametric Clustering

DP-Means HDP 클러스터링 기법을 활용한 비모수적 접근법을 이용하되, 전략 대칭성에 기반하여 학생과 문제의 MVec 임베딩을 공동으로 클러스터링하는 것이다.

이후 전체 데이터가 아닌 생성된 각 클러스터에서 샘플을 선택하여 모델을 훈련함으로써 정확도를 희생하지 않고 확장성을 확보할 수 있다.

• 대칭성(symmetry)에 기반한 비모수적 접근법을 통해 학생과 문제의 MVec 임베딩을 공동으로 클러스터링한다.

• 데이터셋 $D$에 대해, $S$는 학생 집합이고 $P$는 문제 집합이다.

Definition 1. 전략 불변 분할 (strategy-invariant partitioning)

• 분할 $\{S_i\}_{i=1}^{k_1}$와 $\{P_j\}_{j=1}^{k_2}$로 정의.
• 모든 $i$, $j$에 대해:
  만약 $S,S′∈S_i​$이고 $P,P′∈P_j$​라면, $S$와 $S′$은 각각 $P$와 $P′$에 대해 동일한 전략을 따른다.
• $k_1$​: 학생 분할/클러스터의 수, $k_2$​: 문제 분할/클러스터의 수.

• 전략 불변 분할을 통해 전체 데이터가 아닌 각 클러스터에서 샘플을 선택하여 모델을 훈련함으로써 정확도를 희생하지 않고 확장성을 확보할 수 있다.

  • Introduction에서 DNN 모델이 전체 데이터 분포를 기반으로 학습할 때, 다수 그룹에게 편향될 수 있다는 점을 지적한 부분과 관련이 있다.

접근법 공식화

• 학생 집합: $S=\{x_{i1}\}_{i=1}^{N}$, 문제 집합: $P=\{x_{j2}\}_{j=1}^{M}$.

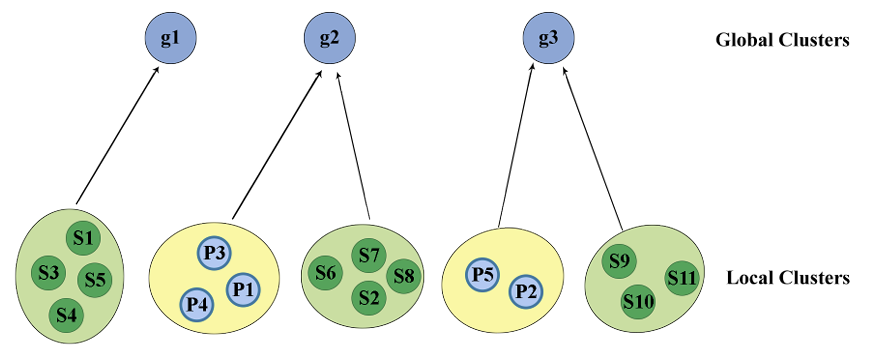
• 로컬 클러스터(Local Clusters): 학생 및 문제 각각의 클러스터.

• 글로벌 클러스터(Global Clusters): 학생 클러스터와 문제 클러스터를 결합한 클러스터.

• DP-Means HDP 클러스터링(2.3에서 다룸)

  $\sum_{p=1}^{g} \sum_{x_{ij} \in \ell_p} \|x_{ij} - \mu_p\|^2 + \lambda_\ell k + \lambda_g g$
  • 전역 페널티 $λ_g$의 값이 클수록 적은 수의 거친(cloarse) 클러스터가 생성되고, 페널티 값이 작을수록 많은 수의 세밀한(fine-grained) 클러스터가 생성된다.

  1. 초기 클러스터링: $\ell_1, \ell_2, \ldots, \ell_g$는 현재의 글로벌 클러스터.

  2. 각 클러스터 내의 전략 대칭성을 기반으로 점수 $S(\ell_1, \ldots, \ell_g)$를 계산한다.

  3. 반복(iteration)마다 점수가 개선될 경우, $λ_g$를 점진적으로 감소시켜 더 세밀한 클러스터를 생성한다. (Coarse-to-fine refinement 접근법)

---

3.3 Refining Clusters using Symmetry

전략을 MVec 임베딩과 위치 인코딩의 조합으로 표현하며, Smith-Waterman(SW) 알고리즘을 이용하여 위치 임베딩 간의 정렬을 계산함으로써 전략 대칭성을 계산하는 것이다.

• 글로벌 클러스터: 각 글로벌 클러스터는 전략 집합을 암묵적으로 나타낸다.

  • 학생-문제 쌍 $(s,p)$이 클러스터에 속할 경우, 이는 $s$가 문제 $p$를 해결할 때 사용한 전략을 나타낸다.

• 클러스터 내 전략 간의 대칭성(symmetric similarity)을 정량화하는 것이 목표이다.
  
  

전략의 근사적 정렬 및 대칭성 계산

• 각 전략은 MVec임베딩과 위치 인코딩(positional encodings)의 조합으로 표현된다.

• 전략에서 특정 KC K를 다음 벡터로 표현:

  $\vec{K} = \vec{K}_e + \vec{K}_p$
  • $\vec{K}_e$​: $K$의 MVec 임베딩.
  • $\vec{K}_p$​: $K$의 전략 내 위치 인코딩.

• 전략 간 대칭성을 계산하기 위해, 우리는 위치 임베딩 간의 정렬을 계산할 때, Smith-Waterman 알고리즘(SW)을 이용한다.

  • 두 시퀀스 간 가능한 최적의 정렬을 계산하기 위해 지역 탐색(local search) 수행한다.

  • 유사도 함수가 필요하며, 두 KC 간의 유사도로, $s(K,K′)=\vec{K}^\top \vec{K}'$으로 설정된다. 즉, $K$와 $K′$의 위치 임베딩 간의 코사인 유사도이다.

  • 정렬에 갭(gap, 비어있는 단계)을 남기는 비용을 나타내는 갭 페널티를 필요로 하며, 대칭성을 갭에 대해 불변으로 유지하기 위해 갭 페널티를 0으로 설정한다.
    즉, 두 전략이 대칭적이라면 전략에 추가 단계를 포함하는 것이 허용하는 것이다.

  • 로컬 정렬에 기반한 스코어링 행렬(scoring matrix)을 반복적으로 계산한다. 최적의 정렬에 대한 스코어를 제공하는 스코어링 행렬을 계산하는 최악의 경우 복잡도는 $O(m \cdot n)$이며, 여기서 $m$과 $n$은 전략의 길이를 나타낸다.

전략 대칭성 정량화 및 클러스터링 대칭성 점수

• 두 전략 $K$와 $K′$ (길이 $n$과 $m$) 간의 대칭성을 SW 알고리즘을 기반으로 정렬 $L(K,K′)$을 통해 계산한다.

  • 정렬에는 $K$와 $K′$ 각각에서 매칭되거나 정렬된 KC 쌍 또는 갭(gap, 즉 $K$의 KC가 $K′$의 어떤 KC와도 정렬되지 못한 경우)이 포함된다.

• $K$와 $K′$ 간의 대칭 점수 계산:

  $r(K, K') = \frac{1}{\max(n, m)} \sum_{(K, K') \in L(K, K')} (\vec{K}^\top \vec{K}')$
  • $(K,K′)∈L(K,K′)$: 정렬된 KC 쌍.
  • $\vec{K}^\top \vec{K}'$: 두 KC의 코사인 유사도. 따라서 $0≤r(K,K′)≤1$.

• 클러스터링 대칭성 추정:

  $S(\ell_1, \ldots, \ell_g) = \frac{1}{g} \sum_{p=1}^g \frac{1}{Z_p} \sum_{K, K' \in T(\ell_p)} r(K, K')$
  • $T(ℓ_p​)$: 클러스터 $ℓ_p​$에 포함된 모든 전략의 집합.
  • $Z_p = \frac{2}{|T(\ell_p)|(|T(\ell_p)|-1)}$​: 정규화 항.
  • $S(ℓ_1​,\dots,ℓ_g​)$의 값이 클수록 $ℓ_1,…,ℓ_g$에 속하는 클러스터링이 높은 전략 대칭성을 가진다.
  • 반복(iteration) 중 대칭성 점수 $S$가 감소하지 않는 한, 또는 고정된 반복 횟수 내에서 $\lambda_g$를 $\epsilon$만큼 감소시키면서 $\lambda_g$를 조정한다.(Coarse-to-fine refinement 접근법)

---

3.4 Training the Model

학생과 문제 벡터를 입력으로 받아 KC 시퀀스를 출력으로 생성하는 One-to-Many LSTM 구조를 사용하여 전략을 예측한다.

4. EXPERIMENTS

4.3 Comparison to Baselines

1. Shakya et al. 의 접근법(CS):
   동일한 데이터셋에서 중요도 샘플링(importance sampling)을 사용해 LSTM을 훈련하는 특화된 접근법.
   다만, 숙련도(mastery)나 근사 대칭성(approximate symmetries)을 고려하지 않아 다양한 훈련 인스턴스를 효과적으로 찾지 못한다.

2. 계층적 샘플링(GS, Group Sampling):
   학생이 해결한 문제의 수에 비례하여 샘플링하는 접근법.

3. 랜덤 샘플링(RS, Random Sampling):
   학생과 문제를 균등하게 무작위로 샘플링하는 단순한 방법.

4. 어텐션 샘플링(AS, Attention Sampling):
   논문에서의 접근법으로, 대칭성과 숙련도를 고려한 샘플링을 수행하는 접근법.

---

4.4 Results and Discussion

Accuracy & Scalability

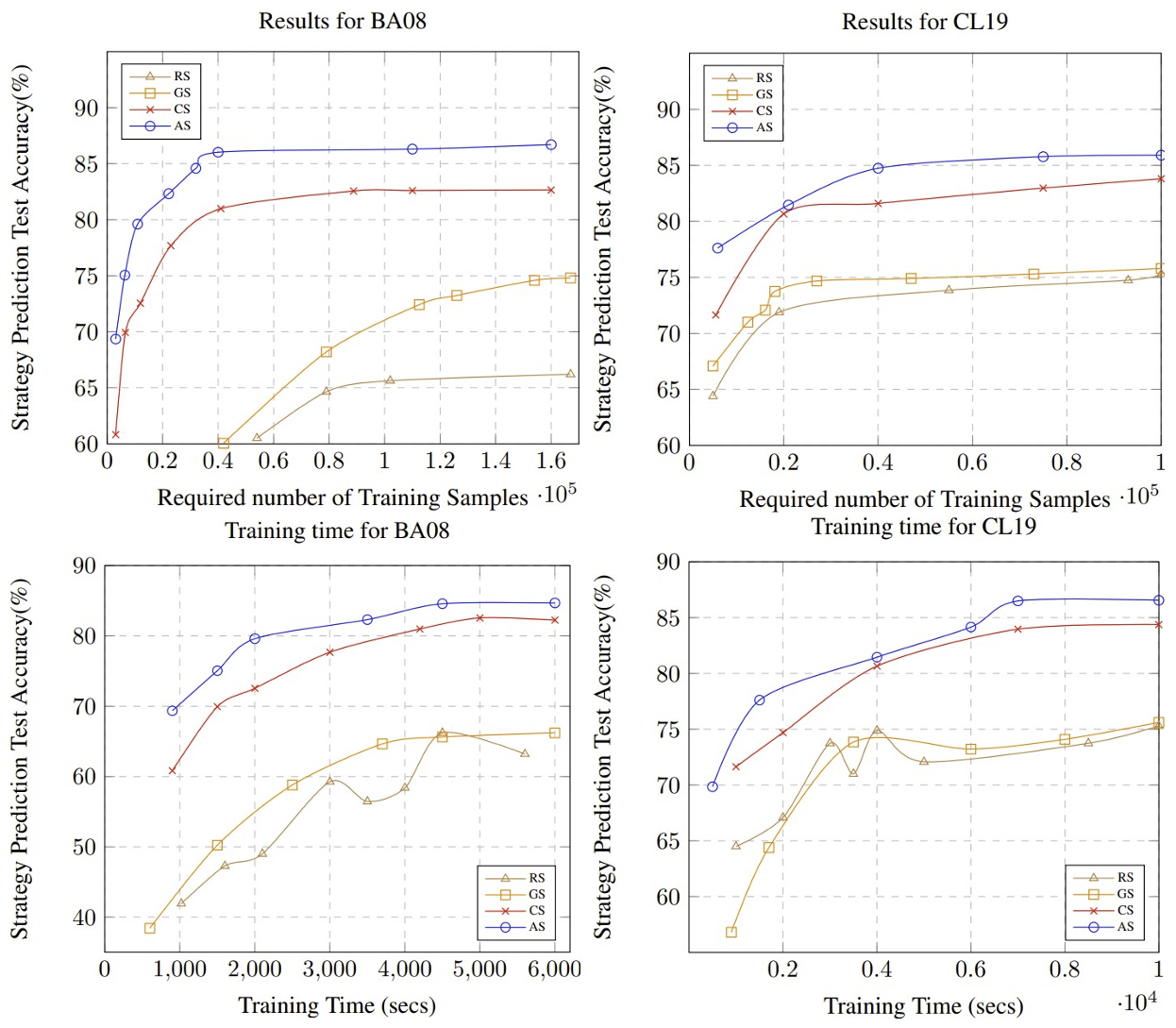
• AS는 BA08 데이터셋(1.6M)의 1% 미만으로 80% 이상의 테스트 정확도를 달성했다.
• AS에서 추가적인 숙련도 임베딩 생성 및 비모수적 클러스터링 처리가 필요했음에도 가장 빠른 성능을 보였다.
• 전체 데이터셋을 사용한 모델 훈련 시도에서 모델 수렴에 실패했다.

---

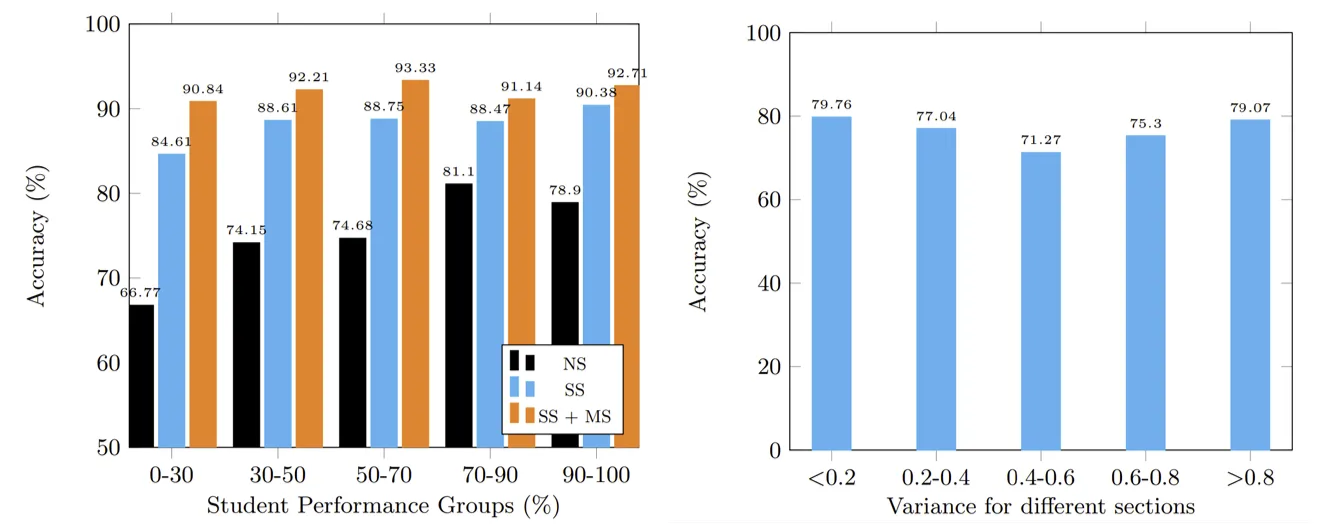
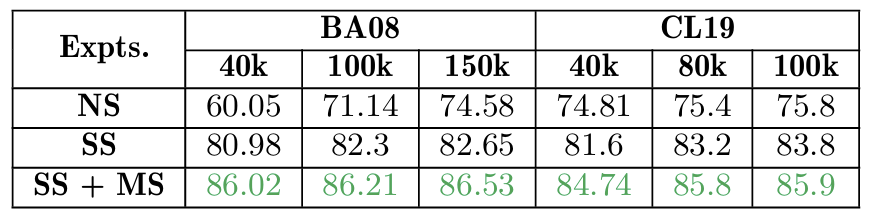
Ablation Study

접근법에 각 구성 요소를 단계적으로 추가하면서, 훈련 데이터 샘플 크기 변화에 따른 테스트 정확도를 관찰했다.

• No Symmetries(NS):
  대칭성을 사용하지 않으며, 클러스터링을 무작위로 수행했다.

• StrategySymmetries(SS):
  대칭성을 사용하되, 숙련도를 이용하여 임베딩을 학습하지 않았다.
  Word2Vec 입력으로 학생($S$), 문제($P$), KC($K$)의 삼중 쌍 $(S,P,K)$만 사용하여 임베딩을 생성했다.

• SS + Mastery(SS + MS):
  대칭성과 함께, 숙련도를 포함하여 MVec 임베딩을 학습했다.

---

Fairness

1. 성취 수준이 다른 학생그룹에 대해 정확도가 크게 다르지 않는지 확인했다.

2. 희귀 전략을 사용하는 하위 문제 그룹에서 차별적 오류가 발생하는지 확인했다.
   문제 섹션을 $𝐸𝑑𝑖𝑡𝐷𝑖𝑠𝑡𝑎𝑛𝑐𝑒$를 이용해 계산한 전략 간 분산에 따라
   5개의 하위 그룹으로 나누었다. ($𝐸𝑑𝑖𝑡𝐷𝑖𝑠𝑡𝑎𝑛𝑐𝑒 = \frac{변화된 단계 수}{총 단계 수}$)