EECS 498-007 Lecture 19 | Generative Models, Part 1

shyoon·2025년 2월 25일

EECS498-007 딥러닝 머신러닝 컴퓨터비전

EECS 498-007

목록 보기

11/13

✍ 해당 시리즈 포스팅은 미시간 대학의 EECS 498-007 강의 내용을 정리한 글입니다.

Supervised vs Unsupervised Learning

그동안 다뤘던 supervised learning과, unsupervised learning의 차이는 무엇일까?

Supervised Learning

Supervised learning은 dataset이 주어지고, 이는 input $x$ 에 대한 output $y$ 로 이루어져 있다. 주된 목표는 해당 $x$ 와 $y$ 셋을 받아서, 입력 $x$ 를 출력 $y$ 로 mapping시키는 함수를 학습하고자 한다.

하지만 이렇게 $y$ 가 주어진 데이터 셋을 구축하기 위해서는, 수집 된 $x$ 데이터에 대해서 사람들이 직접 annotate 해야 한다는 번거로움이 있다. 그동안 배웠던 classificastion, regression, object detection 등을 수행할 수 있다.

Unsupervised Learning

반면, 우리가 $x$ 만 얻고 어떠한 종류의 ground truth를 얻을 수 없는 경우에 정답 레이블 없이 학습하는 unsupervised learning을 활용할 수 있다.

Unsupervised learning의 목표는 이러한 방대한 양의 데이터에서 label 없이도 모델이 알아서 데이터의 구조를 발견할 수 있는 시스템을 구축하고자 하는 것이다.

대표적으로는 다음과 같은 기법들이 있다.

Clustering
- 유사한 샘플끼리 군집을 형성하고, 각각을 클래스로 정의하는 방법 ex) K-Means
Dimensionality Reduction
- 고차원 데이터에서 저차원의 manifold를 발견하여 label 없이도 예측 가능하도록 하는 데이터의 구조를 발견하는 방법 ex) Principal Components Analysis
Feature Learning
- input에 대해서 가장 잘 압축하는 중간층의 latent feature를 찾고, 이에서 원본 데이터를 다시 복원할 수 있도록 학습하는 방법 ex) AutoEncoders
Density Estimation
- 주어진 데이터 포인트들이 어떤 확률 밀도 함수에 따라 생성되었다고 가정하고 그 분포를 추정하는 과정. 데이터의 내재된 구조나 패턴을 이해하는 데 good

Discriminative vs Generative Models

Discriminative Model

Input $x$ 를 받아서 그에 대한 label이 나올 확률을 구한다. 즉, $p(y|x)$ 를 학습하는 것인데, 이는 각 input에 대한 가능한 label들 사이에서 경쟁하는 것과 같다. 이러한 Discriminative한 방식은 대체로 $y$ 가 주어지는 supervised 방식으로 많이 활용이 된다.

이는 만약 우리가 가지는 label 후보값들에 대해 터무니없는 이미지가 input으로 들어오게 되더라도, 무조건 어느 클래스인지 답을 내야 한다. 즉, 차악이라도 선택을 해야 한다.

Generative Model

반면 Generative한 방법은, 그저 주어진 $x$ 에 대한 확률 분포 $p(x)$ (모두 합하면 1)를 학습하도록 하며, 모든 이미지가 probability mass에 대해서 경쟁한다. 이를 학습하려면 이미지에 대한 깊은 이해가 필요하며, 모델은 터무니 없는 input에 대해서는 확률을 매우 낮게 설정하여 reject 할 수 있다.

이는 정말 어려운 이야기인데, 이 이미지가 실제로 존재할 가능성을 숫자로 지정하고, 어떤 이미지가 다른 이미지보다 더 가능성이 높을지를 알려줘야 하기 때문이다.

강아지가 앉은 것 vs 서 있는 것 , 강아지의 다리가 3개인 것 vs 원숭이의 팔이 3개인 것 중 어느 것이 더 그럴듯한지 등 모든 경우의 수에 따라 존재 가능성으로써 표현해야 한다.

Conditional Generative Model

Conditional Generative Model(조건부 생성 모델)은 모든 가능한 label에 대해서 학습이 진행된다. 어떤 카테고리에도 속하지 않는 이미지는 reject되고, 전과는 다르게 label이 주어져서 해당 label 내에서 모든 이미지끼리 확률을 구하게 된다.

이러한 Conditional Generative Model의 $p(x|y)$ 를 학습하는 방식은 Bayes’ rule에 따라 이미 discriminative model과 generative model로 구한 값들을 통해 아래와 같이 구해질 수 있다.

$P(x|y)$ 는 $y$ 가 주어졌을 때 $x$ 의 확률로, 우리가 구하고자 하는 사후 확률(Posterior probability)
$P(y|x)$ 는 $x$ 가 주어졌을 때 $y$ 의 확률로, discriminative model에서 학습하는 우도(likelihood)
$P(x)$ 는 generative model에서 학습하는 $x$ 의 사전 확률
$P(y)$ 는 y의 전체 확률(사전 분포). 이는 train set의 label 수를 세는 것과 같다.

그래서 세 가지 종류의 모델을 활용하여 무엇을 할 수 있을까?

Discriminative Model
- 여태껏 해 왔듯이, 데이터에 label을 할당할 수 있다.
- Label을 갖고 feature learning을 수행할 수 있다.
Generative Model
- 입력 받은 image가 학습에 사용되었던 데이터에 비해 가능성이 매우 낮은 경우 이상치로 판별하는 이상 탐지에서 쓰일 수 있다.
- Label 없이도 feature를 학습할 수 있다.
- 새로운 데이터를 생성하기 위한 샘플링을 수행할 수 있다.
Conditional Generative Model
- Outlier들은 reject하면서 label을 할당할 수 있다.
- Input label에 조건화 된 새로운 데이터를 생성할 수 있다. 예를 들면, 새로운 고양이 이미지나 강아지 이미지를 생성하도록 할 수 있다.

Taxonomy of Generative Models

위는 Generative models의 분류 체계로, 강의에서는 빨간 박스로 쳐진 모델 위주로 수업을 진행하게 된다.

Autoregressive models

Explicit density estimation model에 속하는 autoregressive model에 대해 알아보자.

우선 Explicit density estimation의 목적은 $x$ 와 learnable weight matrix인 $W$ 를 입력으로 받아서 해당 이미지에 대한 density function값을 내보내고자 하는 것이다.

Maximizing weight $W^*$ 는 training data의 probability를 최대화하고, log를 취해서 곱을 합으로 변환하한 후 $p(x^{(i)})$ 를 $f(x^{(i)}, W)$ 로 대체한 후, gradient descent를 통하여 $W$ 를 최적화한다.

이제 Autoregressive 방식에 대해서 자세히 알아보자.

우리의 input data $x$ 가 $x_1, x_2, … , x_T$ 등의 다양한 subparts로 포함된다고 보자. (이미지를 예로 들면, $x$ 는 한 이미지 샘플이고, subparts는 해당 이미지의 픽셀로 볼 수도 있다.)

그렇다면 $p(x) = p(x_1, x_2, x_3, … , x_T)$ 가 되고, 이는 chain rule에 따라서 $p(x_1)p(x_2|x_1)p(x_3|x_1,x_2)... = \prod^T_{t=1}p(x_t|x_1,...,x_{t-1})$ 로 표현될 수 있다.

이러한 조건부 확률을 학습하기 위해 순환신경망 RNN이 사용될 수 있다.

PixelRNN

순차적으로 픽셀을 처리(좌→우, 상→하)하면서 하나의 색을 저장하고, 이전 픽셀들의 정보를 hidden state에 저장한다. 다음 픽셀의 값을 예측할 땐 R,G,B 세 개의 채널 별로 softmax 분포를 예측한다.

하지만 NxN 크기의 이미지에 대해서 2N-1번의 순차적인 step이 필요하다는 점과, RNN의 한계처럼 long-term dependencies를 학습하기 어려워 성능이 제한적이다.

PixelCNN

마찬가지로 코너부터 시작하여 이미지 픽셀을 생성해내는데, 현재 시점의 픽셀을 예측할 때 이전에 만들어진 픽셀값들을 이용하여 softmax loss를 통해 결과를 얻게 된다. 학습 시에는 convolution을 병렬화해서 PixelRNN보다 훨씬 빠르지만 여전히 test 시에는 한 번에 하나의 픽셀을 생성하므로 느리다.

PixelRNN과 pixelCNN같은 autoregressive model의 특징은 아래와 같다.

Explicit하기 때문에 test 시 input image에 대해서 명확한 density function을 얻을 수 있고, 이는 좋은 평가 지표가 되어 생성 모델의 성능 및 품질을 정량적으로 평가 가능토록 한다.
다양성을 많이 갖고, edge, local/global structure를 모델링한다.
Test time에 순차적으로 생성이 이루어지기 때문에 느리다.

Non-variational Autoencoders

Variational Autoencoders를 알아보기 전에 먼저, variational을 뺀, 그냥 autoencoder는 무엇일까?

이는 raw data $x$ 로부터 어떠한 label 없이 feature vectors를 학습하는데, 이는 probabilistic하진 않은unsupervised 방법이다. 일반적으로 해당 $z$ 를 얻는 과정은 CNN을 통해 학습된다.

그래서 raw data로부터 이러한 feature transform을 어떤 방식으로 학습할까?

그 후에 $z$ 를 입력으로 받아서 decoder를 거쳐 기존의 input data를 reconstruct하는데, 이 때 trasnposed convolution 등의 upsampling 과정을 거치게 된다.

그래서 loss는 input $x$ 와 reconstruct 된 input $\hat x$ 의 차이가 되고, 이러한 identity function을 학습하는 부분이 유용하다기 보단, $z$ 가 input $x$ 에 비해서 훨씬 작은 크기의 feature vector를 갖게 되고, 이를 다시 reconstruct 하는 과정에서 학습하는 것이 어떤 의미를 갖게 된다. 이를 위한 bottleneck 구조가 중요한 부분이다.

학습이 끝난 이후엔 decoder는 제거하고 downstream task를 위해 encoder만 사용하고, 경우에 맞춰서이렇게 학습된 feature $z$ 를 transfer learning에 사용한다.

하지만 이런 단순한 Autoencoders는 probabilistic하지 않기 때문에 학습된 모델에서 새로운 이미지를 sampling할 수 없어서 생성 모델로서의 역할을 할 순 없다.

Variational Autoencoders

Variational Autoencoders는 density function 값을 직접적으로 구할 수 없지만, lower bound는 구할 수 있다. 이러한 lower bound를 maximize하는 데 목표를 둔다.

즉, 기존 Autoencoders를 probabilistic하도록 바꾼 모델이고, 기존 autoencoders처럼 raw data $x$ 로부터 latent features를 학습 가능할 뿐 아니라, 모델에서 new data를 생성도 가능하다.

VAE의 동작 원리는 아래와 같다.

학습 데이터 $\{x^{(i)}\}^N_{i=1}$ 는 관찰되지 않은 latent representation $z$ 로부터 생성되었다고 가정
latent vector $z$ 는 데이터 $x$ 를 생성하는 latent factor(이미지를 구성하는 핵심 요소 ex. 고양이의 크기, 방향, 포즈 등)
Encoder에 $x$ 를 입력받아서 출력되는 latent variable $z$ 의 분포( $p_\theta(z)$ )는 보통 표준 가우시안 분포로 가정되어 모델이 복잡하지 않도록 유지된다.

Decoder는 $z$ 가 주어졌을 때 데이터 $x$ 를 생성하는 분포 $p_\theta(x|z^{(i)})$ 를 모델링한다. (Conditional probability) 즉, 평균 $\mu_{x|z}$ , diagonal covariance $\sum_{x|z}$ 를 출력한다. 이는 Neural Network를 통해 구해진다. 이 때 각 픽셀끼리는 independent하다는 가정을 함.

만약 우리가 각 $x$ 에 대한 $z$ 를 관측할 수 있다면 conditional generative model $p(x|z)$ 를 학습할 수 있지만, $z$ 를 관측 불가하므로 아래와 같이 marginalize 해야 한다.

p_\theta(x) = \int p_\theta(x,z)dz = \int p_\theta(x|z)p_\theta(z)dz

여기서 $p_\theta(x|z)$ 는 decoder network로부터 계산 가능하고, $p_\theta(z)$ 우리가 사전에 표준 가우시안으로 정의한 부분이다.

하지만 모든 $z$ 에 대해 적분하는 것은 불가능하여, Bayes’ Rule을 사용한다.

그렇게되면 마찬가지로 분자 부분은 계산이 가능하지만, 여전히 분모 부분은 계산이 불가하다. 이를 어느정도 해결하기 위해서 $p_\theta(z|x)$ 를 근사할 수 있도록 $q_\phi(z|x)$ 를 학습하는 Encoder가 필요하게 된다.

그렇게 $p_\theta(x|z)$ 와 $q_{\phi}(z|x)$ 를 encoder와 decoder를 통해 joint하게 학습하는 구조가 된다.

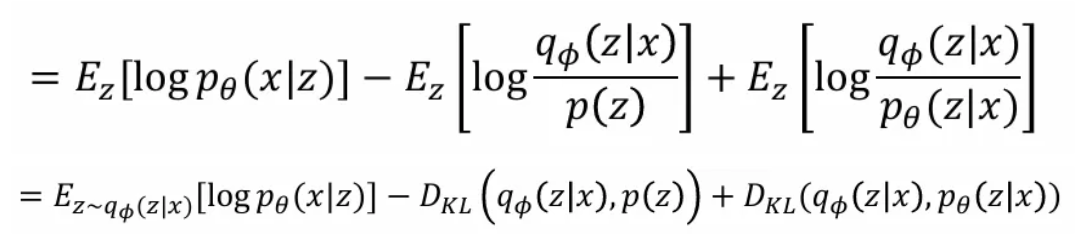
그렇게 $log \ p_\theta(x)$ 는 위와 같이 근사할 수 있다. 이렇게 얻은 마지막 식에서 첫 번째 term은 data reconstruction, 두 번째 term은 prior와 encoder network로부터 얻은 sample의 KL divergence를, 마지막 세 번째 term은 encoder와 decoder의 posterior의 KL divergence를 의미한다.