
✍ 해당 시리즈 포스팅은 미시간 대학의 EECS 498-007 강의 내용을 정리한 글입니다. cs231n 강의와 유사하여 해당 시리즈 포스팅과 겹치는 부분이 많이 있을 수 있습니다.
Problem of FCN in Images
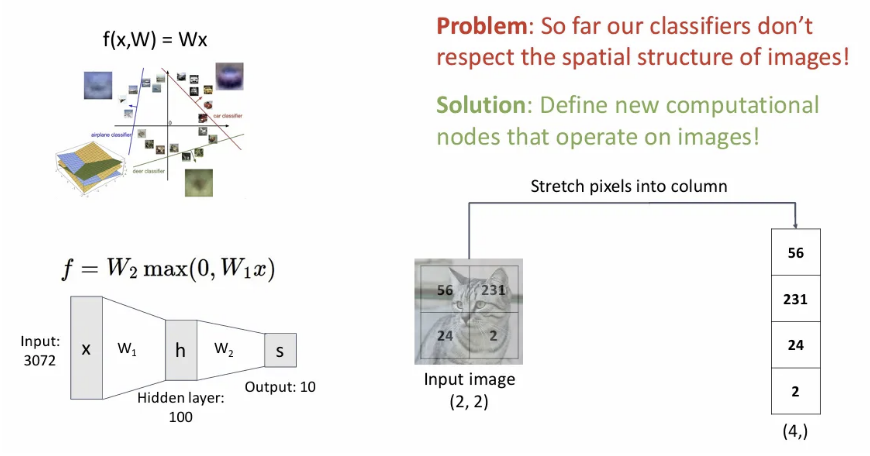
지난 시간까지 배웠던 FCN 구조에 우리는 입력 이미지를 그림과 같이 flatten해서 하나의 벡터로 집어넣었다. 하지만 이는 이미지의 가장 큰 특징 중 하나의 spatial structure 정보를 파괴하는 행위이다.
이미지의 spatial structure를 잘 활용하기 위한 새로운 계산 방식이 필요하다.
Fully-Connected Layers to Convolution layers
지금까지 FCN layer와 activation function에 대해 다뤘었다면, 이제 이미지를 위한 convolutional neural network와 이에 관련된 추가 기본 연산들에 대해 다뤄본다.
Fully-Connected Layer
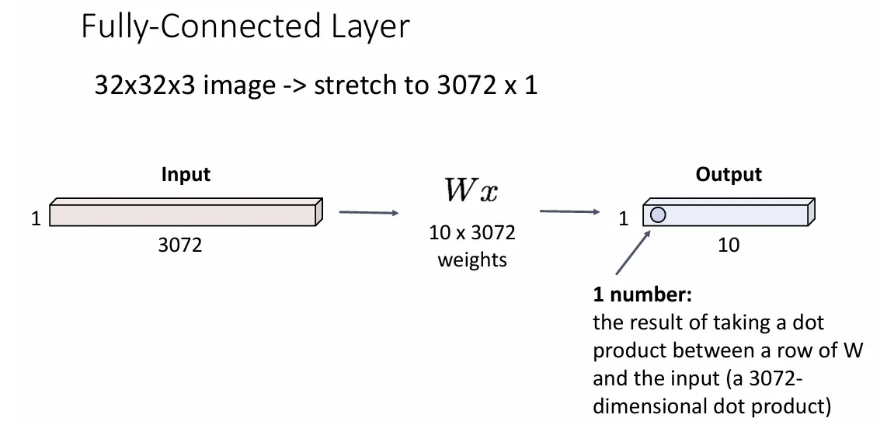
다시 한 번, 이미지를 입력받았을 경우, 예를 들어 32x32x3 이미지를 입력 받으면 이를 flatten하여 3072 길이의 벡터로 만들어서 FCN의 입력으로 집어넣게 되고, weight matrix 와 곱해져서 output으로는 역시 클래스 길이의 어떤 벡터를 얻게 된다.
Convolution Layer
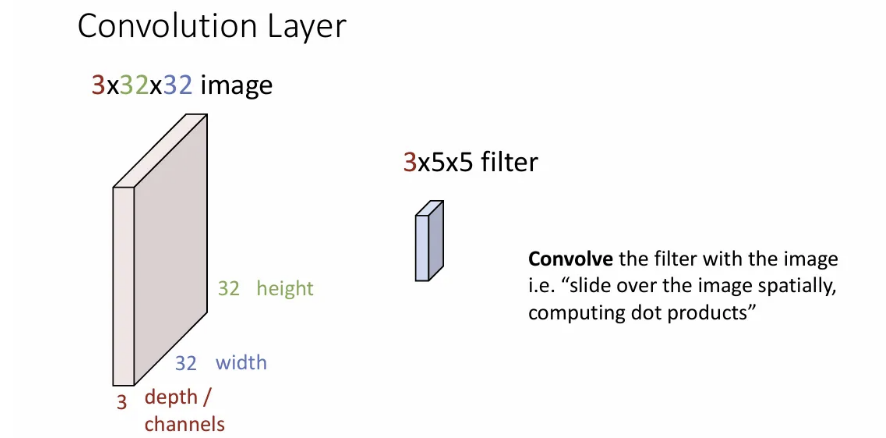
이제 알아볼 convolution layer는 이미지를 그대로 3차원 volume 입력으로 받아서 같은 depth를 갖고, 작은 크기의 width와 height를 갖는 filter로 입력 이미지의 모든 공간 위치에 걸쳐 슬라이딩해가며 계산을 수행하게 되는데,

이 계산은 필터와 이미지가 겹치는 구간에서 dot product를 해서 하나의 scala값을 얻는 연산이 된다. (사실 bias 값을 더해주는 것도 포함되지만 보통 그림에서는 생략함)
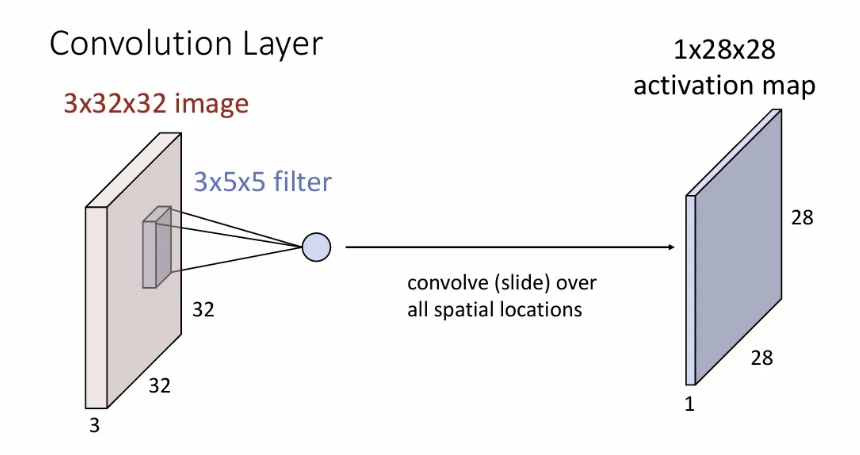
그렇게 입력 이미지의 좌측 상단부터 우측 하단까지 필터를 슬라이딩해가며 내적값을 얻으면 오른쪽과 같은 하나의 activation map이 만들어지게 된다. 여기서 입력 이미지의 width/height보다 activation map의 width/height가 줄어들었는데, 이는 뒤에서 알아보자.
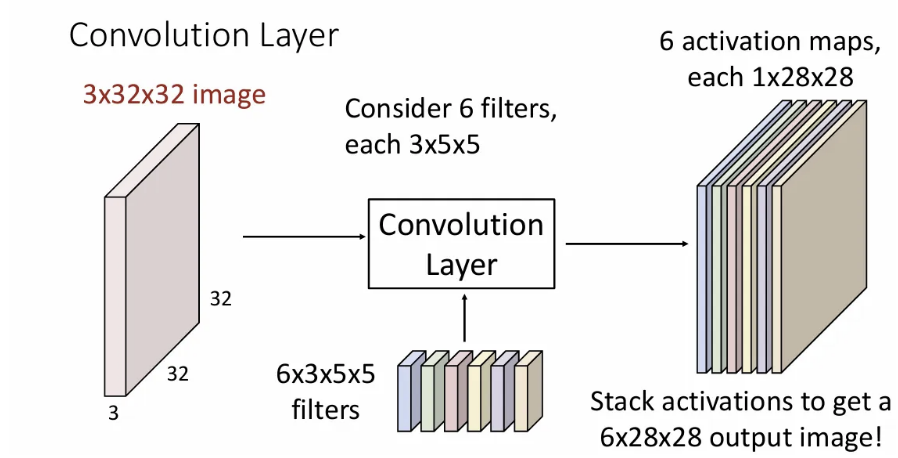
여기서 각 layer마다 다양한 종류의 feature map(activation map)을 얻기 위해서 한 개가 아닌 여러 개의 필터를 사용해서 각각에 대한 activation maps를 얻는다. 위 슬라이드는 6개의 필터를 사용한 예시이다. 결과를 모두 depth 방향으로 concat하므로 shape은 6x28x28이 된다. (단일 3차원 텐서) 각 activation map에는 이미지의 local 정보를 담게 된다. 이는 입력 이미지의 각 spatial position이 각 필터에 얼마나 영향을 받았는 가를 의미한다.
물론 최대한 다양한 관점에서의 activation maps를 뽑기 위해 각 필터(가중치)는 다른 값으로 초기화된다.
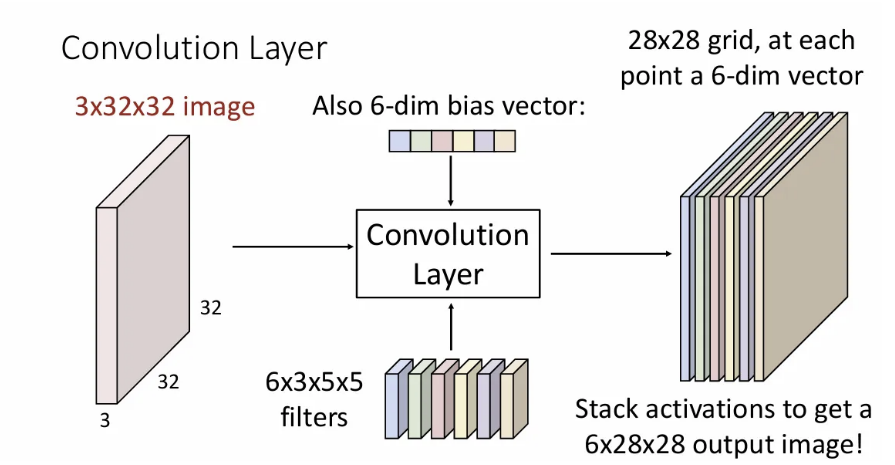
당연히 각 필터 별 bias도 하나씩 있기 때문에 6개 필터면 이는 길이 6의 벡터 형태로 포함이 된다.
이러한 output을 또 다른 관점에서 본다면, 각 point에서 6차원 feature vector를 가진 28x28 grid로 생각할 수도 있다.
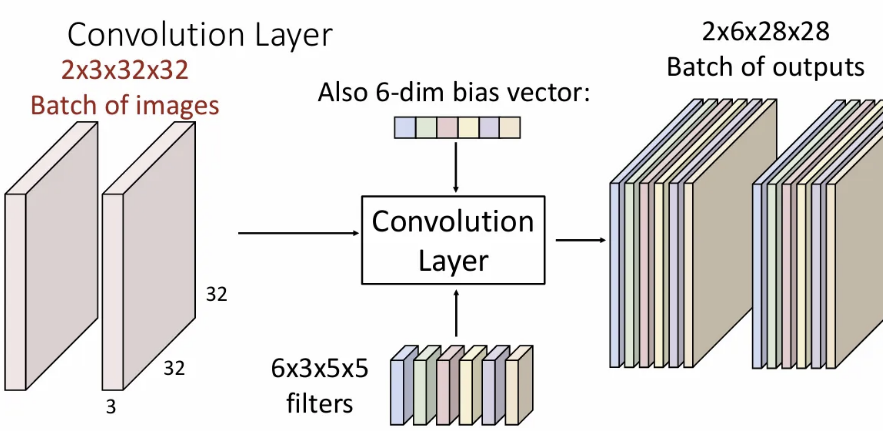
그리고 일반적으론 이미지 배치 단위로 입력하기때문에 3차원 텐서 → 4차원 텐서로 그룹하여 연산을 진행하게 된다.
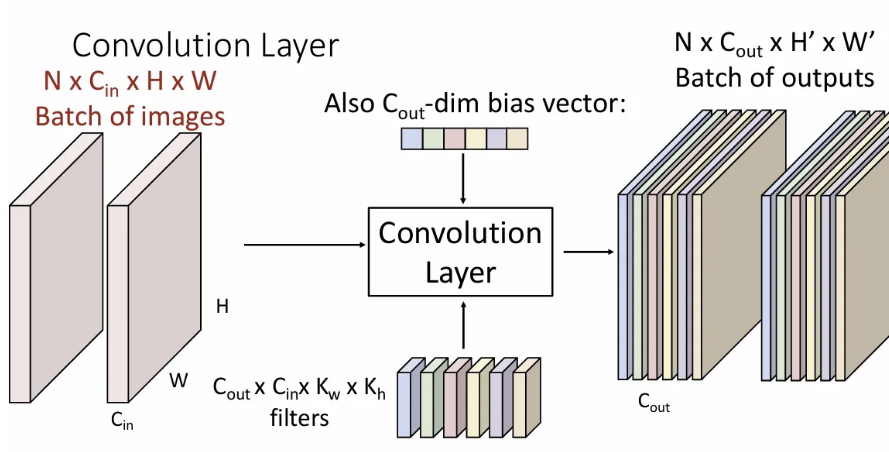
위 슬라이드가 일반적인 input / filter / output 의 shape이 된다. 차원과 차원은 다를 수 있는데, 은 filter 개수와 같은 차원으로 정해진다. 도 convolution 시 어떤 방식으로 연산을 하느냐에 따라 와 같아질수도, 달라질수도 있다.
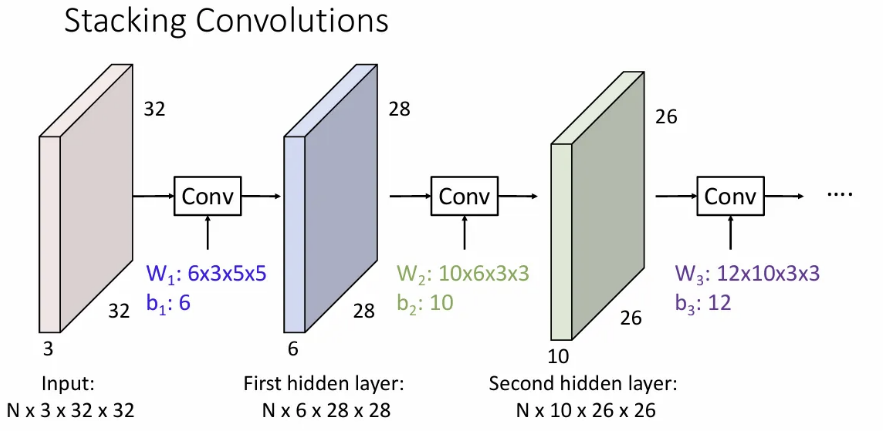
그림과 같이 conv layer에 있는 필터 수 만큼의 output이 나오게 된다. (첫 번째 conv layer의 필터가 6개이면, 두 번째 conv layer의 activation map 수는 6개)
그리고 각 layer의 input과 output이 되는 각 activation maps는 hidden layer라고 불리게 된다.
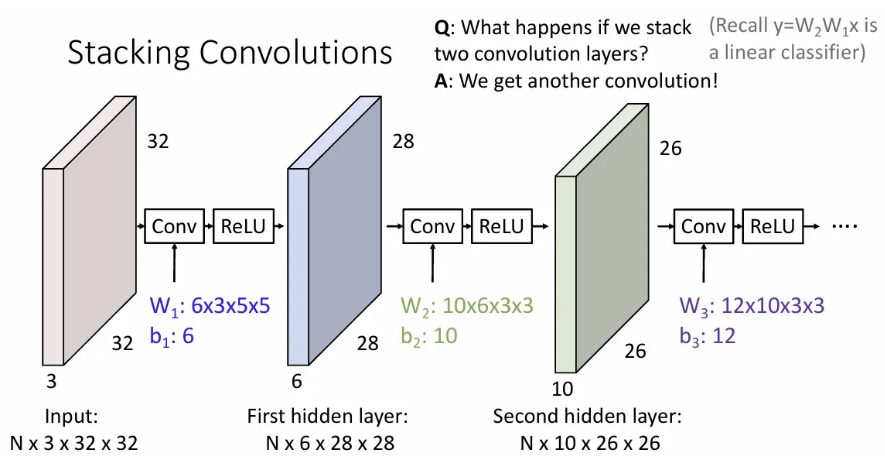
물론, Two-layer MLP때 처럼, conv layer 뒤에 conv layer를 직접 쌓게 되면 이는 linear operator에 지나지 않으므로 마찬가지로 activation function(위에선 ReLU)을 취해주어야 한다.
Visual Viewpoint
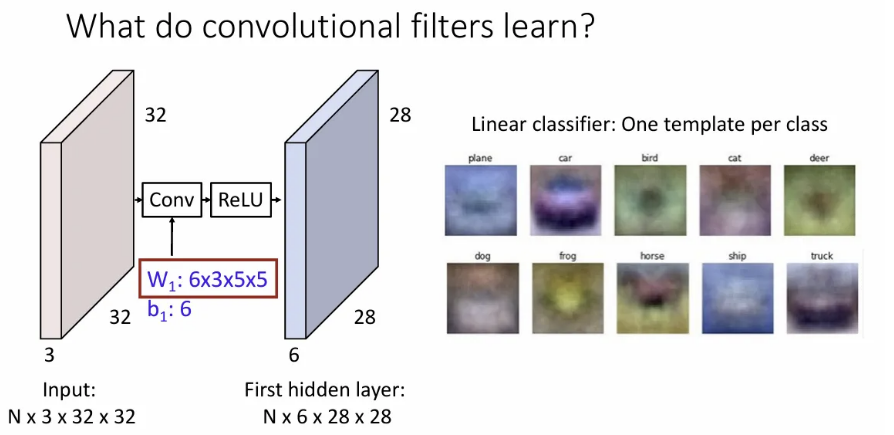
복습해보면, linear classifier에서는 각 클래스 별 하나의 템플릿을 학습했고,

Two-layer neural network에서는(첫 번째 layer만 본다면) 첫 번째 hidden layer의 크기와 같은 개수의 여러 가지 템플릿을 학습하였고, 이를 두 번째 layer에서 종합하였다.
그렇다면 conv layer에서 각 필터는 무엇을 학습할까?
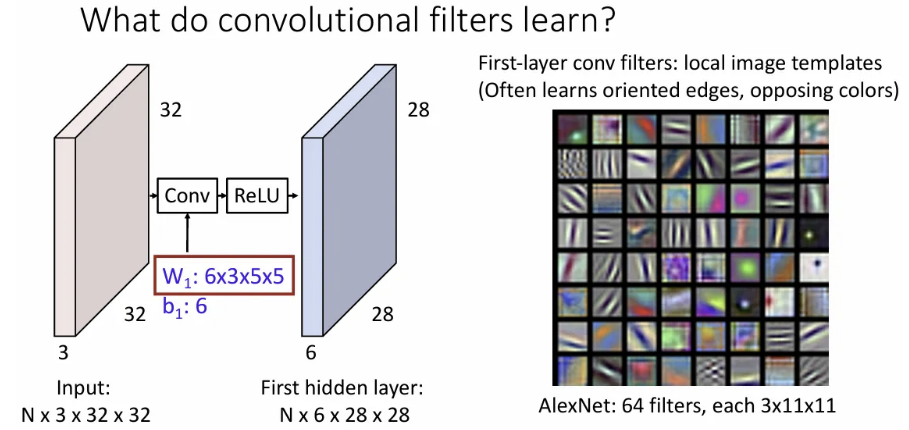
ImageNet으로 사전학습 된, ConvNet의 일종인 AlexNet의 첫 번째 layer의 conv 필터를 시각화 한 결과이다. 이미지에서 oriented edge나 opposing colors(보색) 등을 학습한 것으로 유추할 수 있는데, 이런 정보들을 이용하여 입력 이미지의 각 position이 다음 hidden layer에 영향을 미치는 정도를 학습한다고 보면 될 듯하다.
A Closer Look at Spatial Dimensions
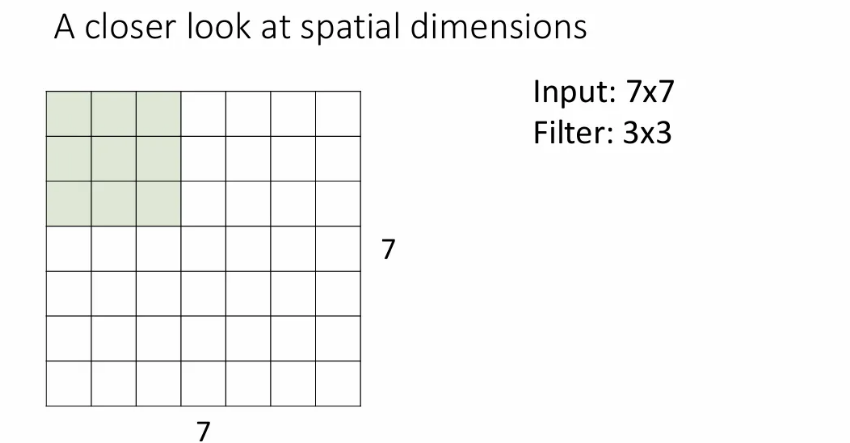
7x7 크기의 이미지에 3x3 필터로 conv연산을 하는 과정을 살펴보자.
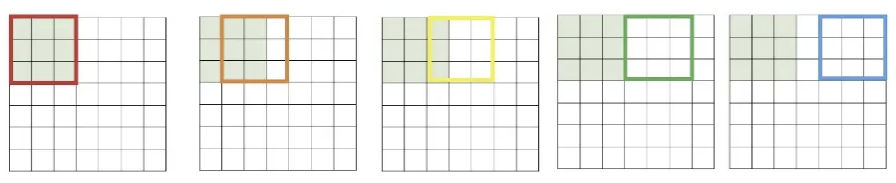
Stride(이동 픽셀)를 1로 지정하고 width방향으로 이렇게 5번 슬라이딩되고, height 방향으로도 마찬가지라서 결과는 5x5가 나온다.
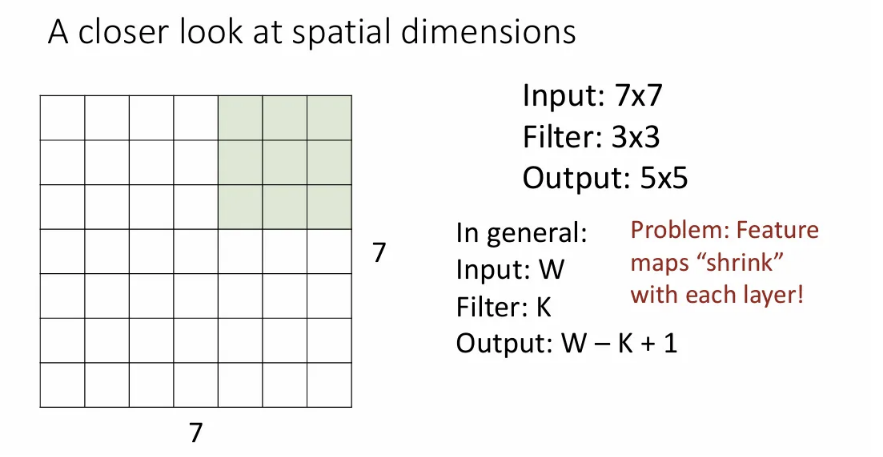
이는 (가로, 세로 길이 같다고 가정) - (커널 크기) + 1로 일반화가 가능한데, 이런 연산을 반복하게 되면 한 layer를 거쳐갈 때 마다 feature map 크기가 줄어들게 된다.
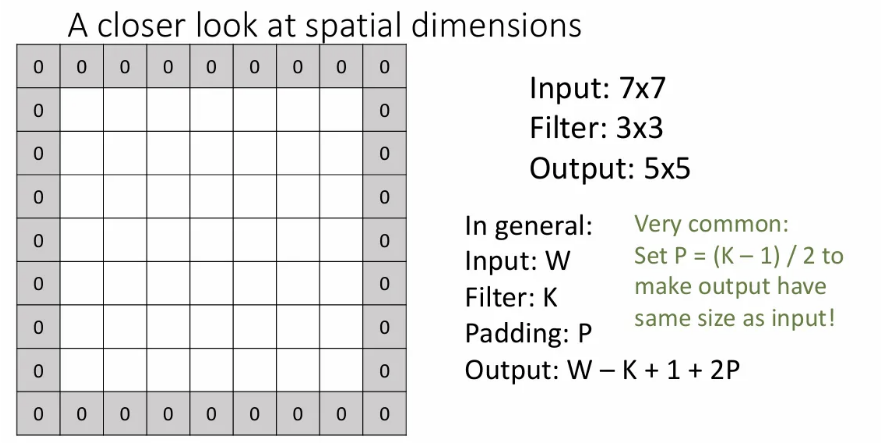
만약 feature map(activation map)의 크기가 줄어들지 않기 바란다면, 다음과 같은 padding 기법으로 이를 방지할 수 있다. input에 위와 같이 0값을 갖는 픽셀들로 감싸는 것이다. 여기서 감싸는 겹 수를 로 설정하게 되면 output은 가 된다. 필터가 3x3이면 를 1로 설정하면 되고, 5x5면 2로 설정하면 feature map 크기를 유지할 수 있다. 이를 same padding이라고 한다.
Padding을 할 때 가장 근접한 픽셀 값을 복사해오는 방법도 있겠지만, 그냥 편하게 zero padding을 쓰면 웬만하면 잘 작동하는 것 같다.
Receptive Fields
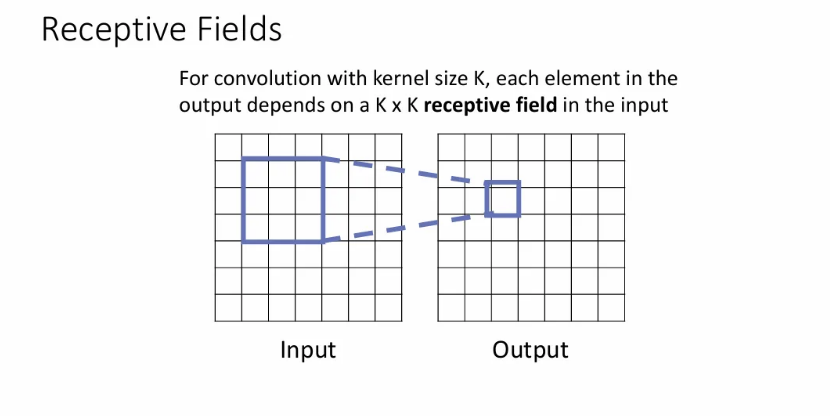
Conv layer가 무엇을 하는지 생각해볼 수 있는 또 다른 방식인데, 이는 output의 각 spatial position이 input에서 어느 정도의 region에 의해 영향을 받는 지를 의미한다.
Output 픽셀은 해당 픽셀과 동일한 위치 기준 input의 크기의 receptive field의 영향을 받게 된다.
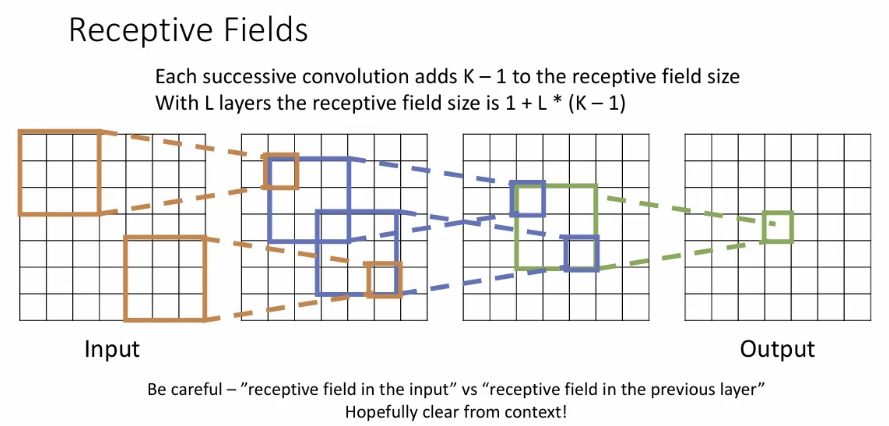
이를 연쇄적으로 살펴보면, 최종 output에서 한 픽셀은 input의 매우 큰 공간 영역에 따라 달라진다는 것을 확인할 수 있다.
위의 3-conv layer를 예시로, output의 한 텐서의 다음 receptive field는 3x3이 되고, 그 다음은 5x5, 그리고 최종으로 7x7까지 확장된다. 이는 로 일반화될 수 있다.
하지만 매우 높은 해상도의 이미지를 입력으로 받게 될 때, output의 한 텐서가 입력 이미지의 큰 영역을 볼 수 있도록 하려면 매우 많은 conv layer를 쌓아야 가능하다.
위 예시는 7x7을 input으로 받을 때 kernel size가 3이면 출력의 한 텐서에서 3 layers 만으로도 input의 모든 영역을 볼 수 있지만, 1024x1024 이미지를 입력으로 받게 된다면 kernel size 3 기준으론 512개는 되는 conv layer를 쌓아야 할 것이다..
이를 해결하기 위해 또 다른 다양한 방식으로 downsampling 해주어야 한다.
Strided Convolution
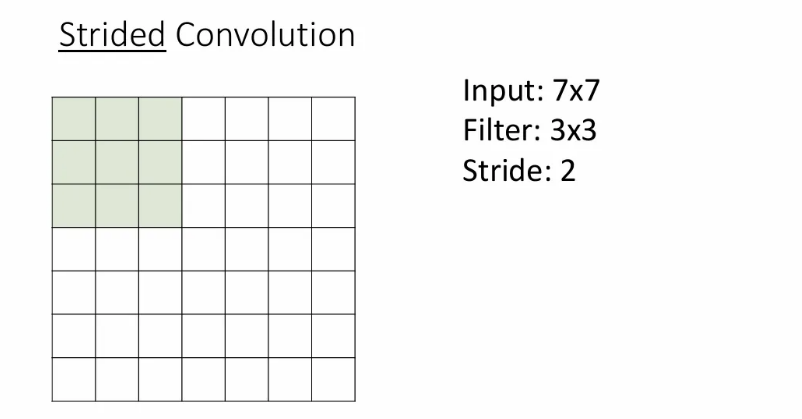
만약 같은 예시에서 stride(보폭)를 2로 설정하게 된다면, conv는 아래처럼 수행된다.
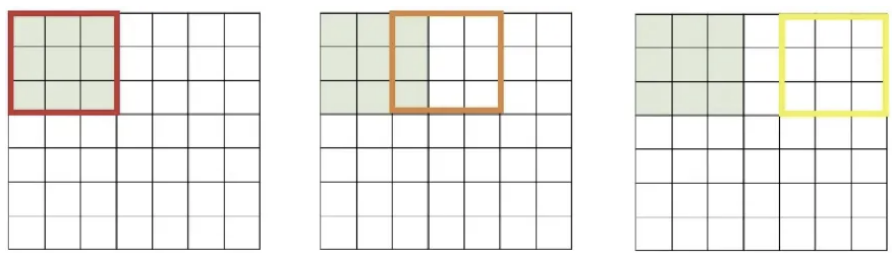
stride를 2로 바꿔서 conv를 수행한 결과는 3x3이 나오게 된다.

이를 공식화하면 위 슬라이드와 같이 표현될 수 있다. stride를 늘린 conv layer를 추가하면 한 layer 내에서 receptive field를 효과적으로 늘릴 수 있다.
이처럼 conv 연산에는 다양한 하이퍼파라미터들이 있고, 이를 통해 원하는 모양의 output을 낼 수 있다.
1x1 Convolution
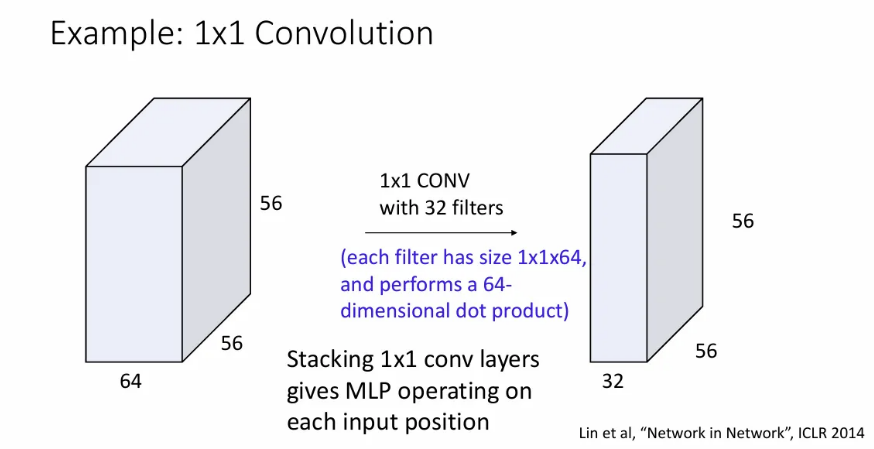
1x1 convolution도 가능한데, input의 depth만큼의 내적 연산을 수행해서 하나의 activation map을 얻게 되고, 필터 수로 출력의 채널 차원 수도 지정될 수 있다.
이는 input에서 각 feature vector마다의 linear layer와 같고, 각각의 feature vector가 input 원소인 Fully Connected Neural Network로 볼 수 있다.

Convolutional Network에서 흔히 사용되는 하이퍼파라미터 세팅 및 공식이니 참고.
Other types of Convolution
1D Convolution
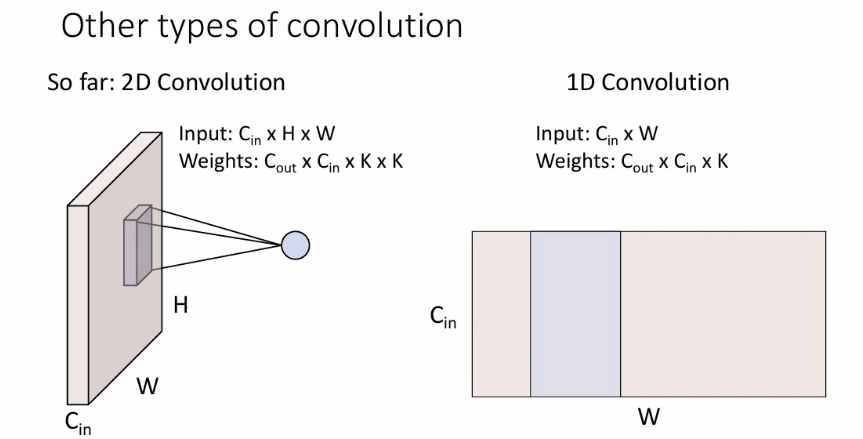
2차원의 input(하나의 spatial dimension과 하나의 channel dimension)을 받아서 convolution을 진행한다.
Sequence 형태의 텍스트나 오디오 데이터를 처리할 때 많이 사용된다.
3D Convolution
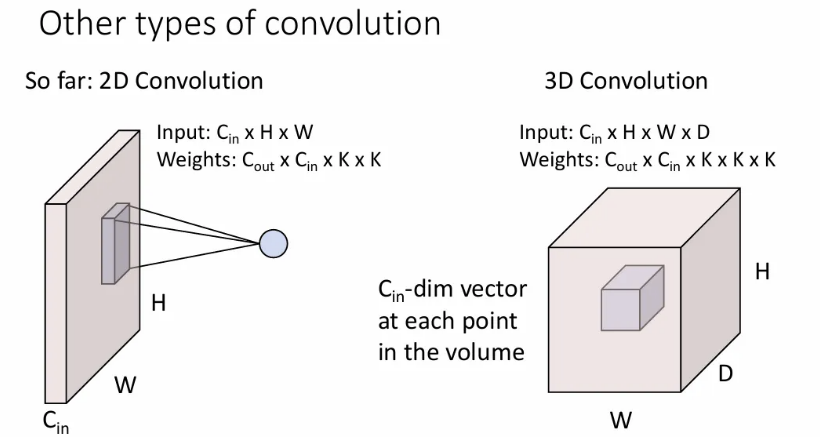
배치의 각 요소는 4차원 텐서가 된다(3개의 spatial dimension과 하나의 channel dimension으로 이루어짐). Weight matrix(커널)은 모양을 갖는다.
Point cloud data나 3D data를 다룰 때 사용된다.
Pooling Layers
Parameter에 대한 학습을 포함하지 않는 방식으로 신경망 내부에서 downsampling을 할 수 있는 pooling layer에 대해 알아보자.
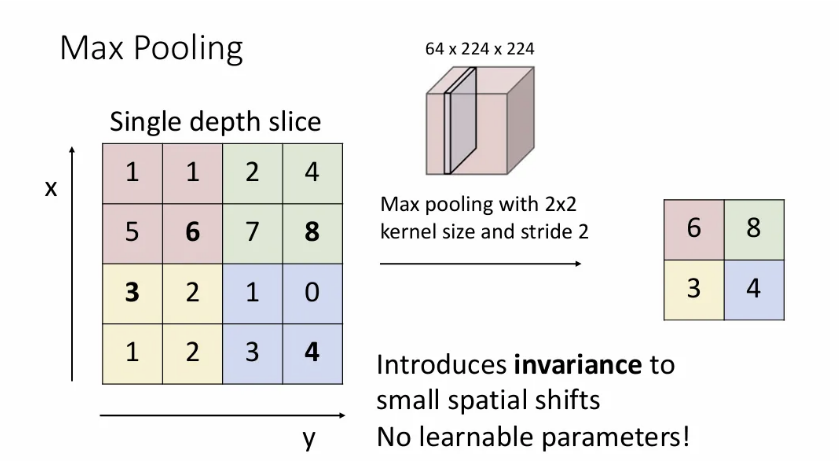
각 커널에서 최대값만 취하는 방법이 max pooling이다.
만약 kernel size를 2x2, stride를 2로 맞추게 되면(보통 pooling region이 겹치지 않도록 둘을 같게 설정한다.) 각 2x2 pooling region에서 max값들만 가져와서 붙여준다.
빨간 region은 max값인 6으로 축소된다는 의미이다.
이렇게 downsampling에 pooling을 선호하는 이유는 learnable parameter가 필요없고 max pooling의 경우 작은 spatial shift에 어느정도 invariance를 도입하기 때문이다.
→ 각 pooling region에서 가장 큰 값을 선택하는데, 이미지에서 어느 객체의 위치가 조금 변하더라도 해당 영역 내 최대값은 변하지 않을 확률이 높기 때문.

위는 pooling에 대한 요약.
Classic Architecture
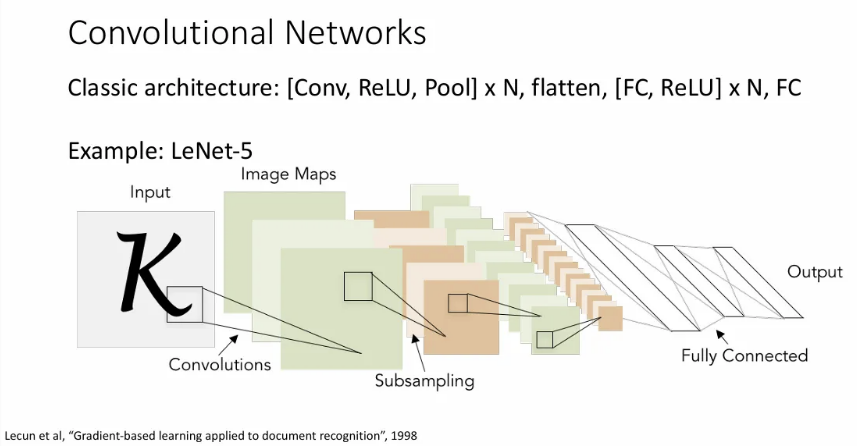
전통적인 CNN 구조는 위처럼 Conv → ReLU → Pool layer를 여러개 거친 뒤, flatten해서 fully-connected layer + ReLU layer를 여러 개 지나고, 마지막으로 fully-connected layer로 최종 output을 내는 구조를 갖게 된다.
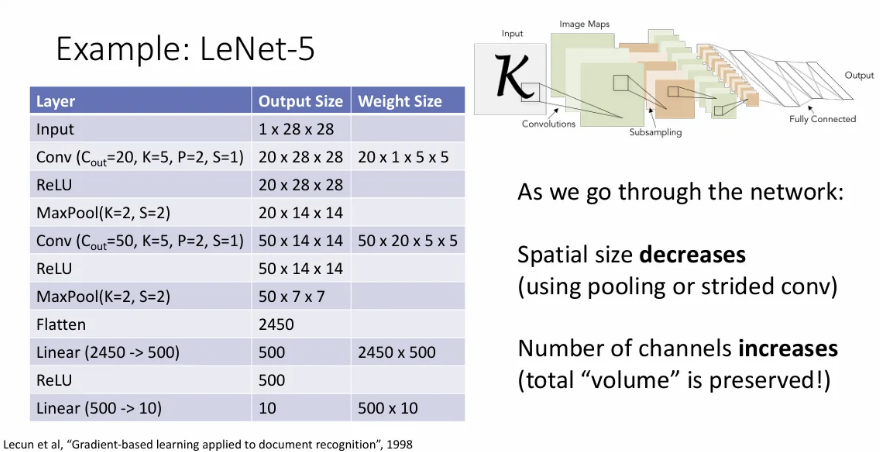
과거 글자 인식에 사용되었던 LeNet-5 구조를 보면, conv layer를 거칠수록 spatial size는 감소하지만 channel 수는 증가해서 전체적인 데이터의 크기는 유지되는데, convolutional network의 일반적인 특징이다.
사실 max pooling만으로도 non linearity를 주입할 수 있지만 굳이 ReLU를 또 넣지는 않아도 된다곤 한다. 하지만 일반적으로는 max pooling 뒤에도 ReLU를 넣는 구조를 많이 쓴다고 한다.
Normalization
하지만 위에서 소개한 layer들 만으로는 CNN은 쉽게 global optima로 수렴하지 않는다. 이를 해결하기 위해 normalization 기법을 도입하였다.
Batch Normalization
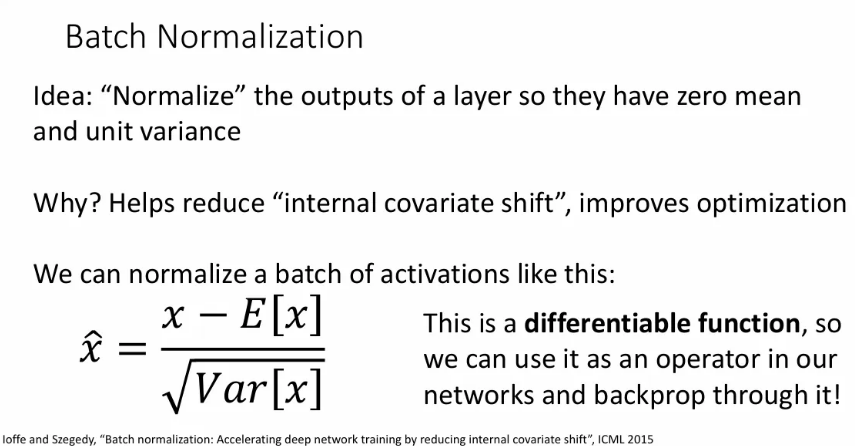
대표적인 방법이 바로 batch normalization이다.
이전 계층에서 출력을 받아서 이를 표준 정규분포로 정규화하는 layer이다.
이것이 “internal covariate shift”라는 것을 줄이고, 이는 최적화를 개선한다고 한다.
정확히 무슨 의미인지는 모르지만, DNN을 학습할 때 각 계층은 입력 계층의 출력을 보게 되는데, 이 모든 가중치 layers는 동시에 학습되어 해당 layer의 output의 분포가 바뀌어 최적화에 방해가 되고, 이러한 분포의 변화로 인한 악영향을 줄이기 위해 standardization한다는 것 같다.
이 표준화 식 자체가 미분 가능해서, network 중간 중간 껴 넣기만 하면 된다.

크기가 인 개의 벡터로 구성된 배치를 입력 받는다고 할 때, 벡터 차원의 각 요소를 따라(화살표) 배치 내 각 요소에 대한 empirical 평균, 분산을 계산하고 표준화 한다.

이런 정규화는 지나친 제약 조건이 될 수 있기 때문에, 최종으로는 learnable한 와 로 네트워크가 각 요소에서 보고자 하는 평균과 분산이 무엇인지 스스로 학습할 수 있도록 한다.

하지만 train 시에는 각 미니 배치 별 와 값을 알고 사용하지만, 실제로 test 시에는 test 셋의 미니 배치 별 , 로 정규화를 한다는 건 불가능하다. 따라서 train 에서 쓰였던 모든 미니배치의 와 값의 평균을 사용해서 정규화를 해준다.

그리고 이 test time의 , 는 상수이기 때문에 test 시의 batch normalization은 linear operator가 되고, 이는 이전 fully-connected나 conv layer와 결합될 수 있다.

ConvNet에서의 batch normalization은 spatial dimension에 대한 normalization도 진행한다는 점이 fully-connected networks에서의 batch norm과의 차이점이 된다.
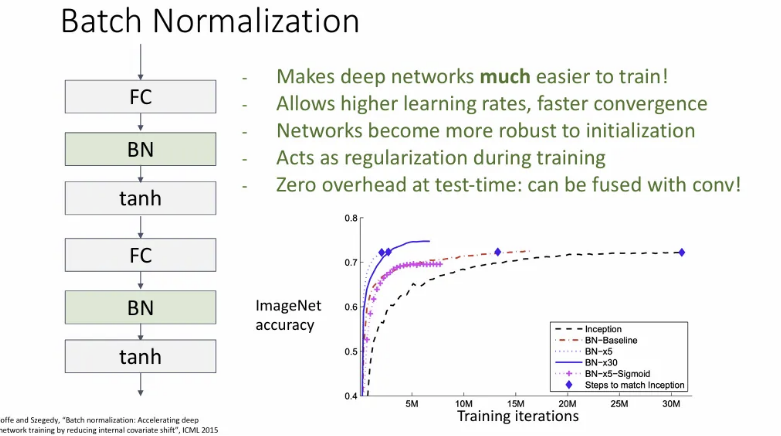
보통 Batch Normalization은 Fully-connected layer가 Conv Layer 바로 뒤 activation function을 적용하기 전에 취해준다.
Layer Normalization

Batch Normalization과는 다르게 train과 test에서 모두 똑같이 동작한다. 배치 내 같은 요소끼리의 평균과 분산이 아닌, 한 샘플 내 feature 차원 에서의 평균/분산으로 정규화를 진행한다. RNN과 Transformers에서 사용된다.
Instance Normalization
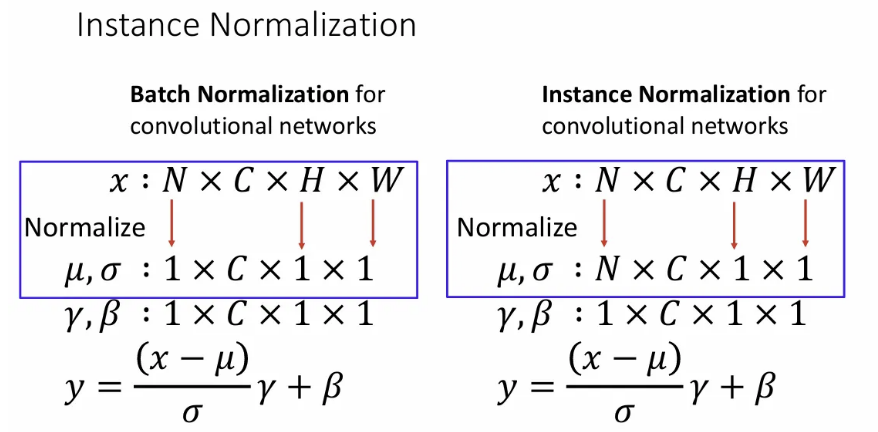
Layer Normalization과 유사한데, 한 샘플에서의 spatial dimension에 대해서 평균과 분산으로 정규화한다. convolution network 버전이라고 생각하면 될 것 같다.
Group Normalization
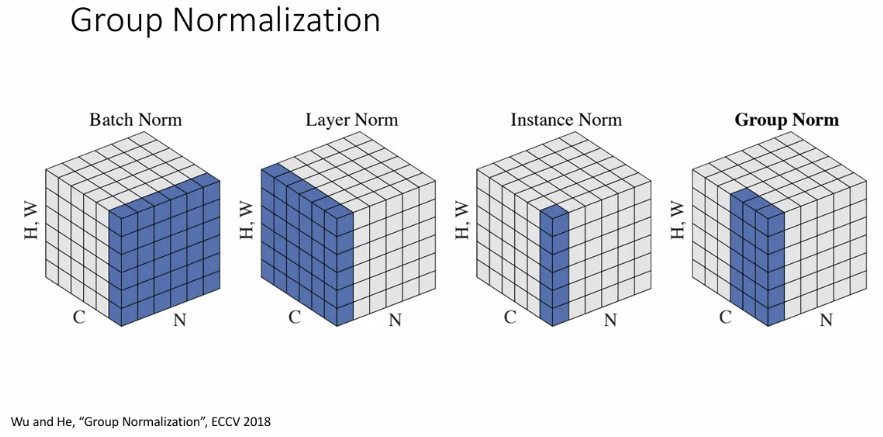
channel dimension을 특정 그룹으로 나누고 이 그룹에 대해서 normalization을 진행하는데, object detection 등에서 잘 작동한다.