
✍ 해당 시리즈 포스팅은 미시간 대학의 EECS 498-007 강의 내용을 정리한 글입니다. cs231n 강의와 유사하여 해당 시리즈 포스팅과 겹치는 부분이 많이 있을 수 있습니다.
개인적으로 이해하기 많이 어려운 챕터였던 것 같다..
How to compute gradients?

그래서 지난 시간까지 배운 gradient descent 기반 최적화를 학습에 적용하기 위해, 어떻게 gradient를 계산할 수 있을까?

이 편미분 값들을 직접 종이에 대고 계산한다면?
- 계산해야 할 값이 너-무 많다.
- Neural Net 구조나 손실 함수가 바뀐다면 처음부터 다시 계산해야 함
- 복잡한 모델에 절대 실현 불가
Computational Graphs
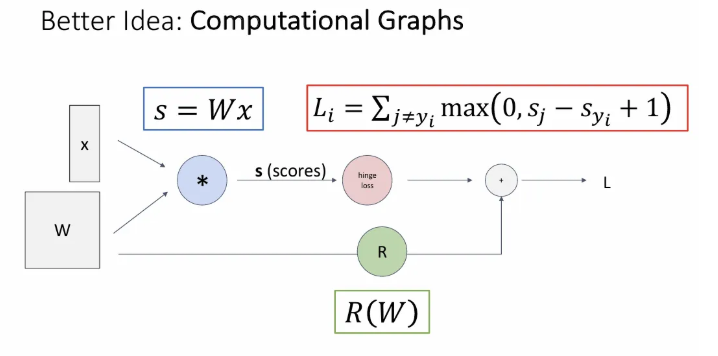
이를 편하게 계산하기 위한 방법이 computational graph(계산그래프)인데, 함수의 연산 과정을 node(계산 노드) 와 edge를 갖는 그래프 형태로 나타내는 것이다.
위 슬라이드에서 제일 왼쪽엔 우리의 데이터 와 learnable matrix 가 주어지고, 이 둘을 입력으로 받는 파란 노드는 두 입력의 matrix multiplication을 의미한다. 다음 빨간 노드는 SVM Classifier의 hinge loss이고, 마지막으로 초록색 노드 regularization term인 와 합 연산되어 전체 loss 이 계산된다.
computational graph를 사용해서 함수를 표현하게 됨으로써 backpropagation 사용이 가능하다.
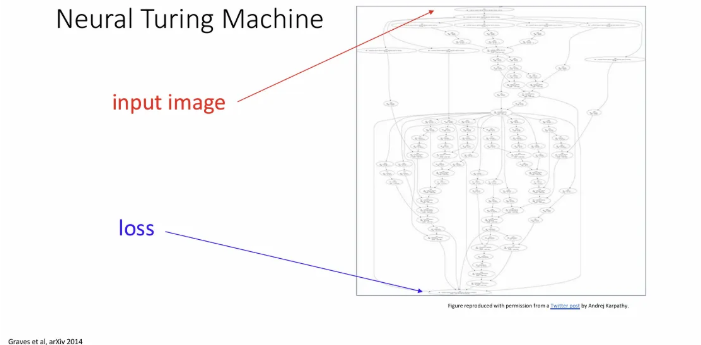
직전 슬라이드같이 간단한 구조에서는 굳이 계산 그래프를 활용할 필요가 없어 보이지만, 다양한 최신 Neural Network 처럼 복잡한 구조에서 모든 계산을 손으로 직접 하려면 매우 복잡해지므로 우리는 꼭 computational graph를 활용하게 된다.
위 슬라이드는 Neural Turing Machine의 계산 그래프인데, 이 복잡한 식을 직접 손으로 계산한다면 매우 끔찍함
Backpropagation
Simple Example
간단한 예시를 통해 backpropagation을 알아보자.
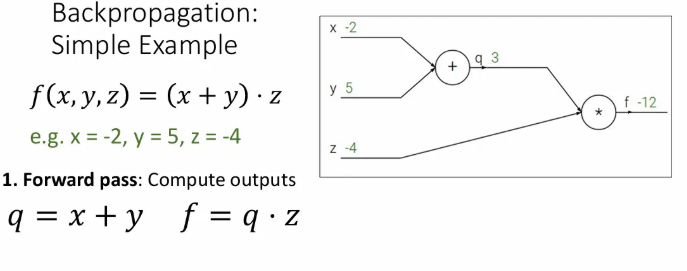
라는 전체 함수가 라는 세 개의 입력을 받아서 를 수행할 때, 를 또 하나의 작은 함수 로 표현 가능하고, 그렇다면 는 로 표현 가능하다. 단순히 이를 계산하는 과정을 forward pass라고 한다.
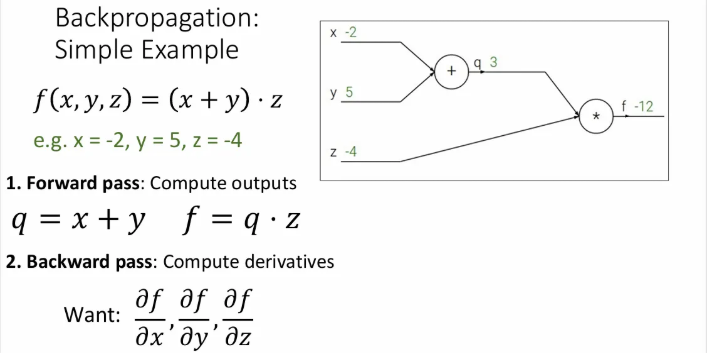
그렇다면 이제 에 대한 모든 편미분 값을 계산하기 위해 backward pass를 해야 하는데, backpropagation이므로 오른쪽에서 왼쪽(뒷 방향)으로 진행된다.
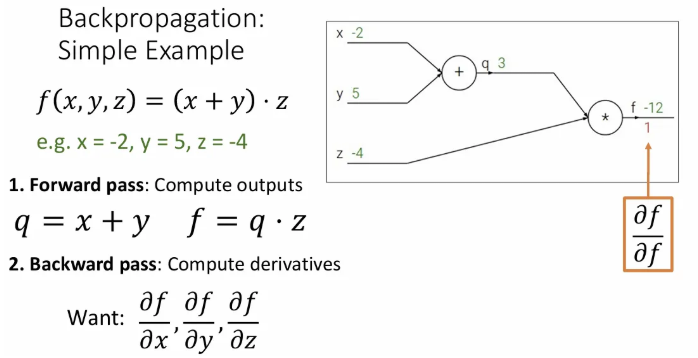
가장 오른쪽인, 자신에 대한 의 편미분 값은 몇으로 시작할까?
당연히 1이다.
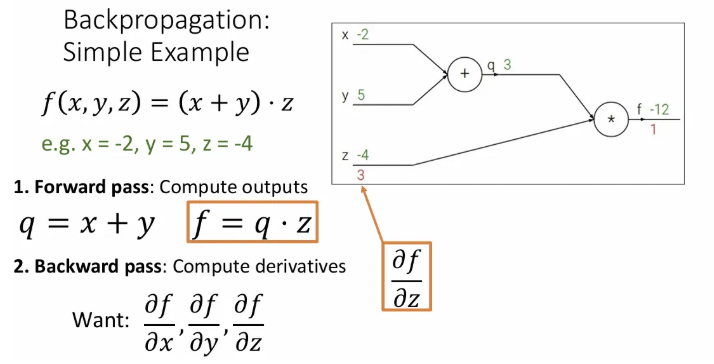
이제 마지막 와 연결되어있는 와 에 대한 편미분 값을 구해야 한다. 먼저 에 대한 의 편미분 값부터 구해보면, 이는 가 되고, 값은 3이었기 때문에 이는 3이 된다.
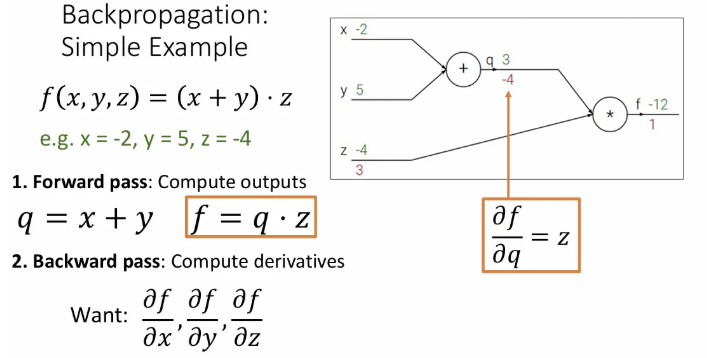
그렇다면 이번엔 에 대한 의 미분값을 구해보면 가 되고, 이는 -4이다.
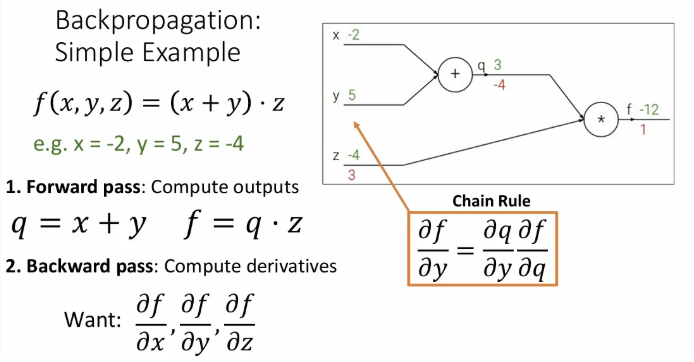
이제 와 직접적으로 연결된 노드의 편미분값은 모두 구했는데, 그렇다면 에 대한 의 편미분값은 어떻게 구할까? (부터)
→ chain rule을 활용해서 에 대한 의 미분값과 좀전에 구해놓았던 에 대한 의 미분값을 곱하면, 자연스럽게 에 대한 의 미분값을 구할 수 있게 된다.
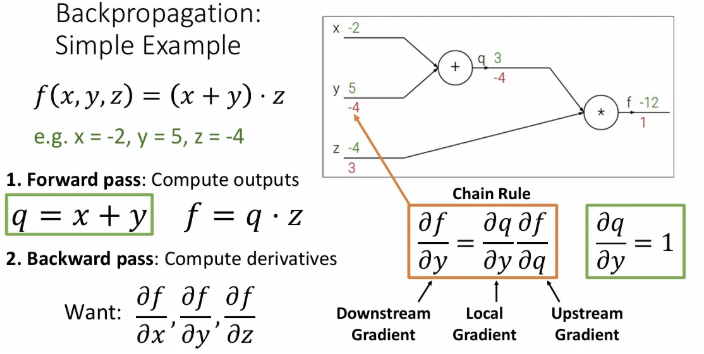
에 대한 의 미분값은 1이고, 에 대한 의 미분값인 -4와 곱하면 이는 -4가 된다.
만약 우리가 에 대한 의 미분값인 downstream gradient(와 는 멀리 떨어져 있다.)를 구한다면, 로부터 직전까지 거슬러 내려온 gradient인 를 upstream gradient라고 하고, 를 local gradient라고 한다.
다시 정리하자면,
- Downstream gradient: 현재 step인 의 변화가 최종 output 에 미치는 영향
- Local gradient: 현재 값이 다음 step의 변수에 얼마나 영향을 미치는 지에 대한 local 정보
- Upstream gradient: 현재 시점에서 다음 step의 결과 값인 가 최종 output 에 미치는 영향
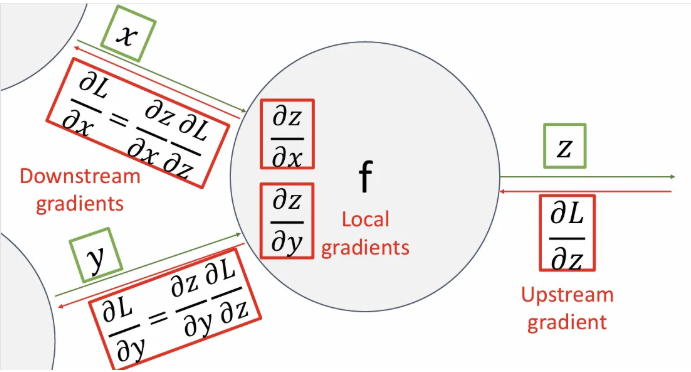
이처럼 현재 노드 연산이 최종 output에 얼마나 영향을 미치는가에 대한 큰 틀에서 고민할 필요 없이, 바로 위까지 흘러내려온 upstream gradient와 현재 시점의 local gradient를 곱하기만 하면 바로 downstream gradient를 얻을 수 있고, 이를 제일 하류까지 반복해나가면 network의 모든 gradient를 계산할 수 있다.
Another Example
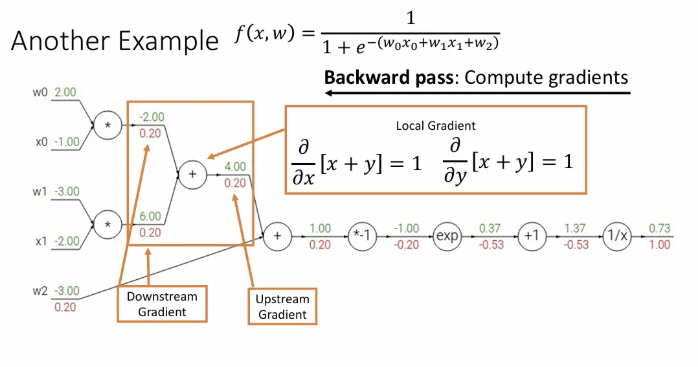
위처럼 이전보다 복잡한 함수 가 주어져도 방금 짚고 간 upstream gradient, local gradient, downstream gradient를 잘 계산만 해주면 각 노드에서의 gradient를 모두 얻을 수 있다.
이렇게 전체 노드에 대한 gradient를 모두 계산할 수도 있지만, 연산 구조에 대한 여러 생각을 더 해볼 수 있다.
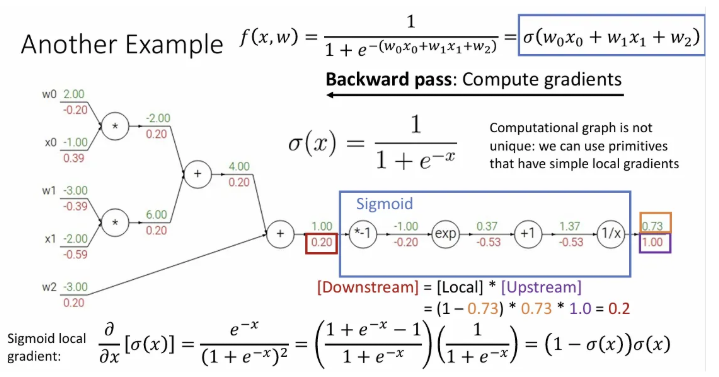
파란색 박스 안의 노드들의 연산을 조합하면 sigmoid function이 된다. 만약 우리가 sigmoid에 대한 미분 값이 라는 것을 알고 있다면 이 자체가 local gradient가 되고, 이를 upstream gradient와 곱하면 한 번에 네 개의 노드에 대한 downstream gradient를 얻을 수 있다.
이 방법은 파란 박스에서 중간 과정의 노드에 값을 저장할 필요 없이 파란 박스의 전체 local gradient를 쉽게 계산할 수 있도록 한다. 계산 과정에도 효과적이고, 함수 자체의 의미도 살릴 수 있다.
Patterns in Gradient Flow
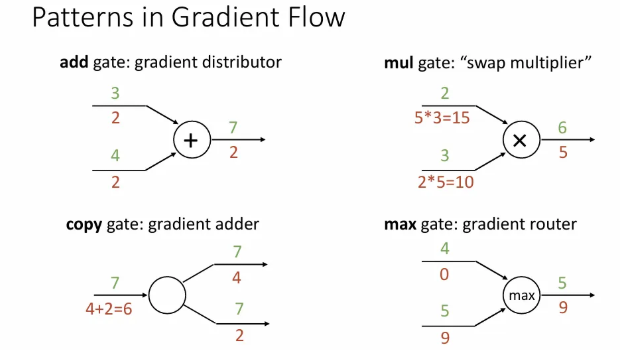
backpropagation의 기본 연산들을 다음과 같은 패턴을 갖는다.
- Add gate: 양쪽 모두 upstream gradient를 그대로 흘려보낸다.
- Mul gate: 두 입력 노드 값을 반대로 곱해서 흘려보낸다.
- Copy gate: downstream gradients를 더해서 흘려보낸다.
- Max gate: 두 입력 노드 중 작은 값은 0을, 큰 값은 upstream gradient를 그대로 흘려보낸다. 최대한 사용하지 않는 게 좋음
Implementation with Flat Code
Backpropagation을 구현하는 “Flat” code부터 살펴보자.
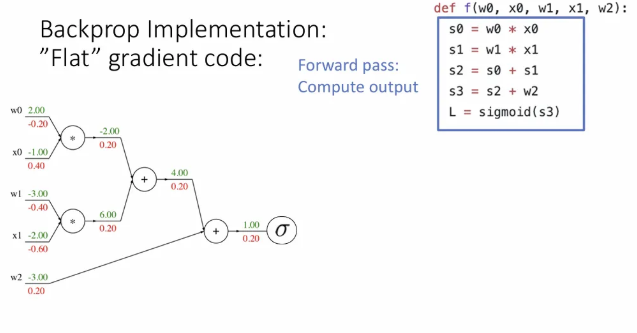
우선 forward pass를 구현한 부분이다. 앞에서 본 예시처럼 sigmoid는 하나의 큰 노드로 묶었다.
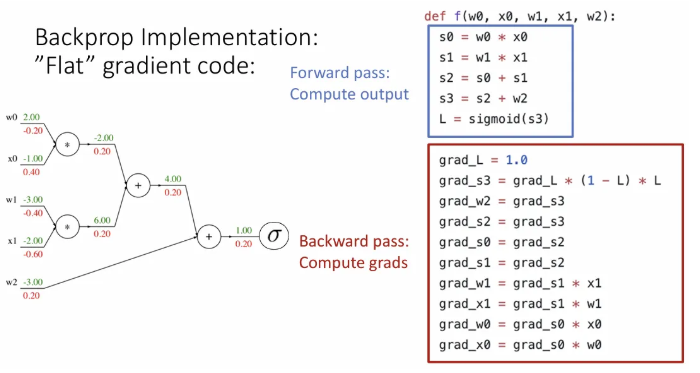
이제 backprop을 위한 부분을 추가했는데, 각 변수들은 각 노드 별 downstream gradient를 저장하고 있다고 보면 될 듯하다.
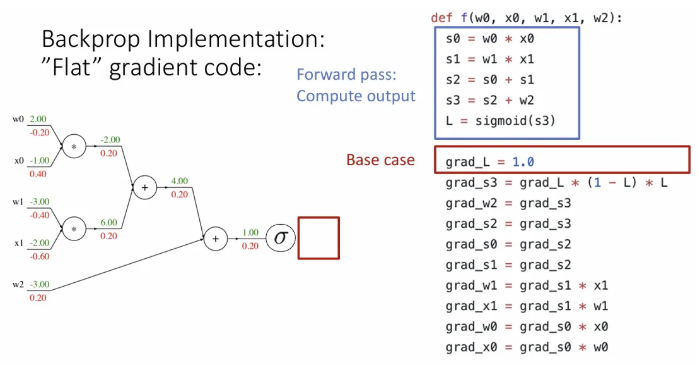
하나씩 순서대로 살펴보면, 처음 grad_L 에는 최종 gradient인 1이 저장된다.
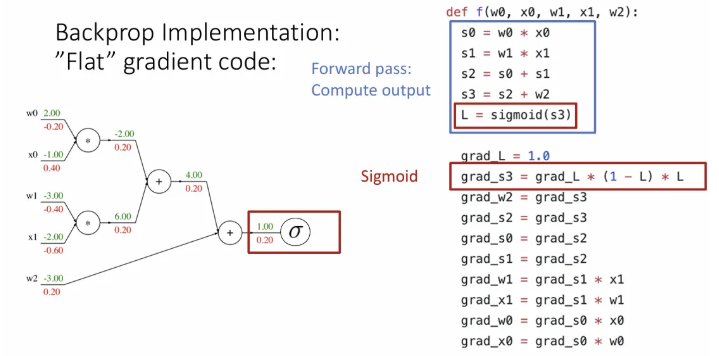
그 하류 grad_s3는 시그모이드 노드의 gradient를 곱한 값이 저장이 되고,
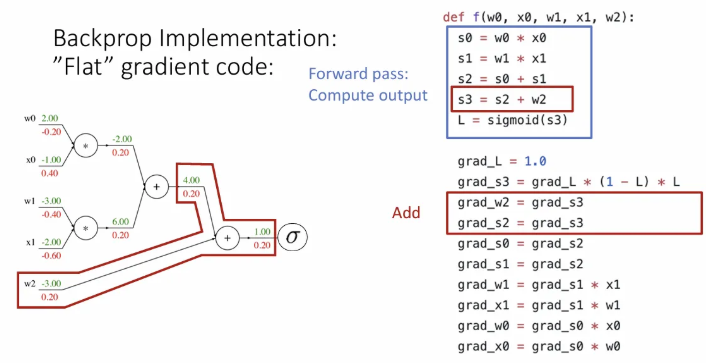
add 노드를 만나서 grad_w2, grad_s2 각 하류로 upstream gradient인 grad_s3를 그대로 전달한다.

다시 한 번 add 노드를 만나서 grad_s0, grad_s1 각 하류로 upstream gradient인 grad_s2를 그대로 전달한다.
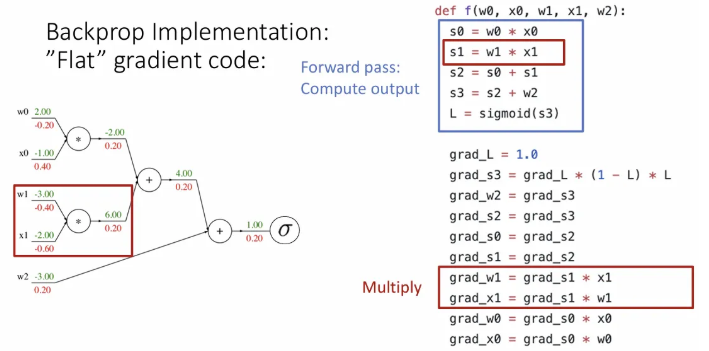
mul 노드를 만나 grad_w1, grad_x1에는 upstream gradient인 grad_s1에 각각 x1, w1을 교차로하여 곱해서 전달하고,

마지막도 마찬가지로 mul 노드를 만나 grad_w0, grad_x0에 upstream gradient인 grad_s0에 x0, w0을 교차로 곱해서 전달하면 전체 gradient 계산이 끝난다.
Implementation with Modular API

하지만 당연히 위에서 구현해 본 flat 방식은 손실 함수의 형태가 조금만 바뀌어도 뒤엎어야 하기 때문에, 실제로는 Modular API로 구현하게 된다.
→ 일종의 계산 그래프 객체를 정의하고 이 계산 그래프 객체는 노드들을 위상 정렬한 후 forward pass, backward pass를 진행한다.

흔히들 연구할 때 많이 사용하는 PyTorch를 예시로 설명한다. torch.autograd.Function을 상속받아서 computational graph에 관한 객체를 만들 수 있다.
forward의 input은 (실제론 보통 스칼라 연산이 아닌 벡터 연산을 하니 torch tensor 형태)와 backprop에 사용되는 값을 저장할 ctx(context)를 입력으로 받게 된다.
backward에서는 forward의 동일한 ctx와 upstream gradient인 grad_z를 받아서 gradient를 구한 후 이를 return한다.
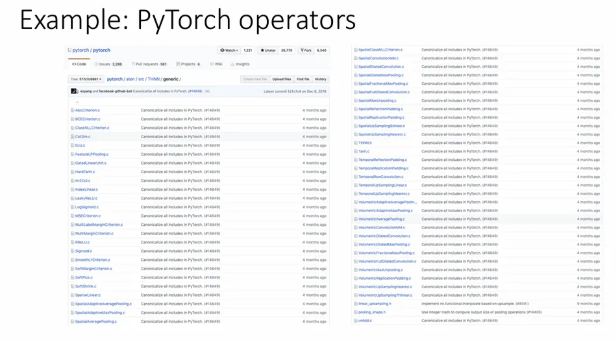
실제로 PyTorch에는 간단한 연산들에 대한 forward, backward가 모두 기술되어 있다.

레포에서 sigmoid에 대한 파일의 코드를 살펴보면 sigmoid function에 대한 forward, backward 함수가 모두 기록되어 있다.
Backprop with Vectors
여태까지는 계산 그래프에서 scalar 연산에 대한 backpropagation만 다루고 있었다면, 벡터 연산은 어떨까?

- Regular derivative(scalar)
- 에 미세한 변화가 생긴다면, 에는 어떤 변화가 생길까?
- 결과는 scalar
- Derivative is Gradient(vector)
- 의 각 요소에 미세한 변화가 생긴다면, 에는 어떤 변화가 생길까?
- 결과는 scalar
- Derivative is Jacobian(Matrix)
- 의 각 요소에 미세한 변화가 생긴다면, 의 각 요소에는 어떤 변화가 생길까?
- 결과는 vector
→ 위 세 개의 예시는 input과 output이 각각 scalar이냐, vector이냐에 따른 도함수의 형태. Input과 output 모두 vector일 때의 backprop을 알아보자.
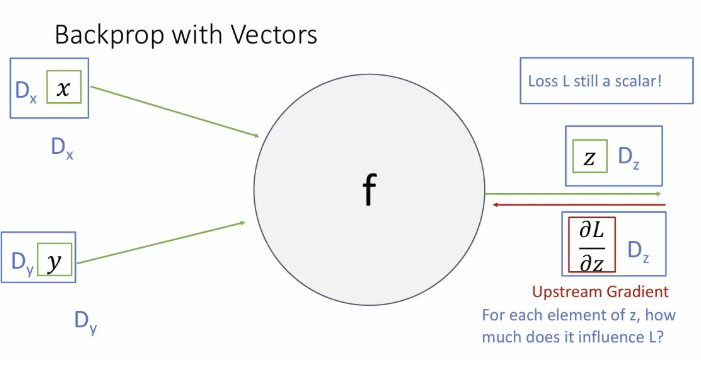
계산 그래프의 중간에서 input으로 들어오는 가 각각 차원 벡터이고, output 는 차원 벡터인 상황이다. Forward pass는 매우 간단하다.
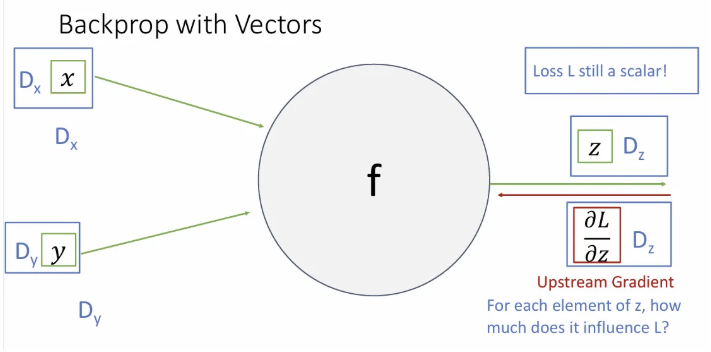
하지만 는 벡터지만 최종 계산되는 최종 loss 은 scalar이고, 이 에 대한 의 편미분(현 시점 upstream gradient)은 차원의 벡터가 된다. 이는 의 각 요소가 미세하게 변화할 때 최종 스칼라 값이 얼마나 변화하는 지를 의미한다.
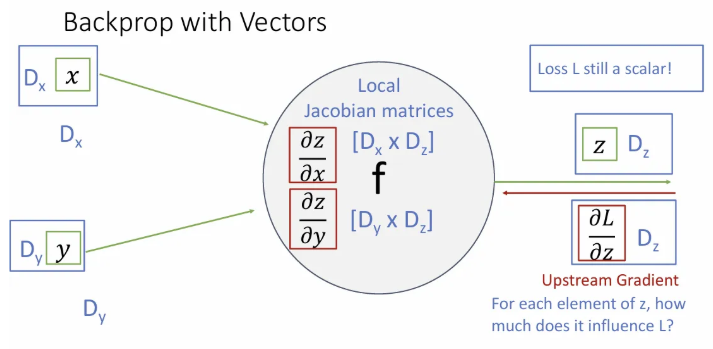
local gradient인 와 는 의 벡터를 의 벡터와 의 벡터로 각각 편미분 한 값이기 때문에 Jacobian matrix들이 된다. (는 의 각 요소가 변화할 때 의 각 요소의 변화를 의미)
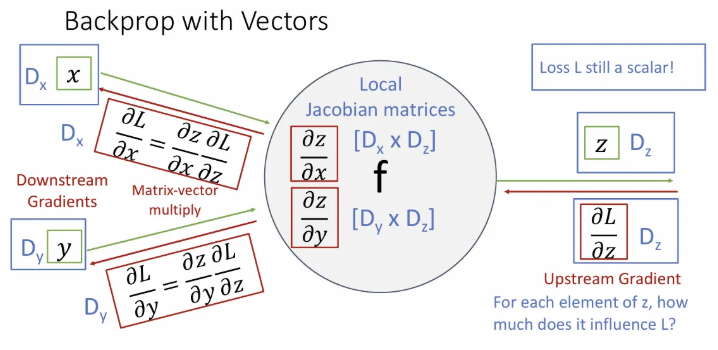
그리고 downstream gradient중 하나인 는 matrix인 와 vector인 를 곱한 의 벡터가 된다. 이는 도 마찬가지. 특정 input에서의 gradient는 그 input 차원과 같다고 생각하자.
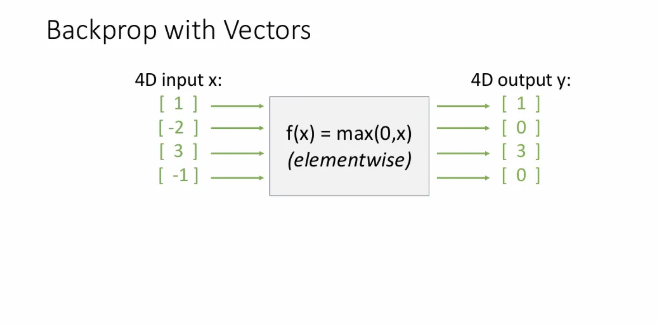
vector 연산 간 backprop의 더 자세한 예시이다. 가 ReLU 함수라고 가정해보자.
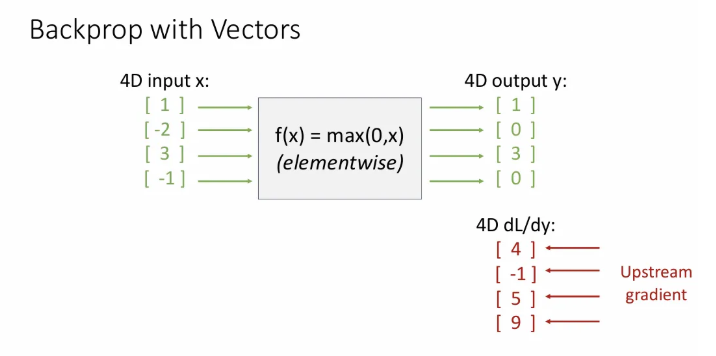
Upstream gradient가 의 벡터였다면 downstream gradient는 얼마가 될까? 위에서 보았던 max gate를 다시 떠올려보면 라는 점을 알 수 있지만,
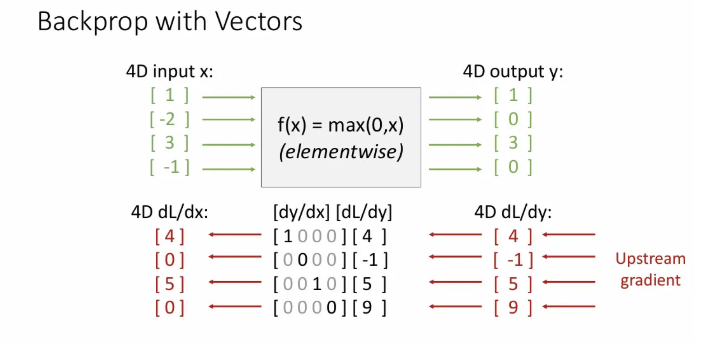
실제로 4x4 크기의 Jacobian matrix 와 곱해져서 해당 결과가 나오게 된다.
위 슬라이드에서 local ReLU gradient에 대한 Jacobian matrix에서도 볼 수 있듯이, 우리가 사용하게되는 대부분의 Jacobian 행렬의 dimension은 아주 크고, 이에 따라 매우 sparse(0이 많이 껴있음)하다. 그래서 이 Jacobian 행렬을 명시적으로 형성하는 경우는 거의 없다.
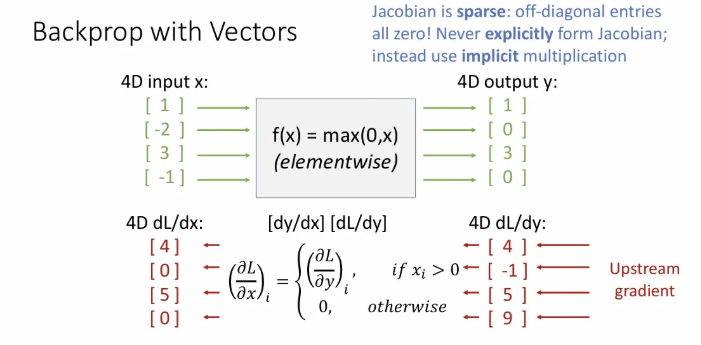
따라서 위 슬라이드처럼 implicit(명시적) multiplication을 사용하게 된다. ReLU의 경우에는 값이 0보다 작으면 모두 0을 뱉는 함수이고, gradient 역시 0이 된다. 그리고 나머지 가 양수인 경우는 값을 그대로 뱉기 때문에 gradient는 1이라서 upstream gradient인 와 1이 곱해져서 는 그대로 이 된다.
Jacobian matrix로 표현할 때 sparse한 부분은 그냥 clipping해서 훨씬 효율적으로 계산한다는 것 같다..
Backprop with Matrices
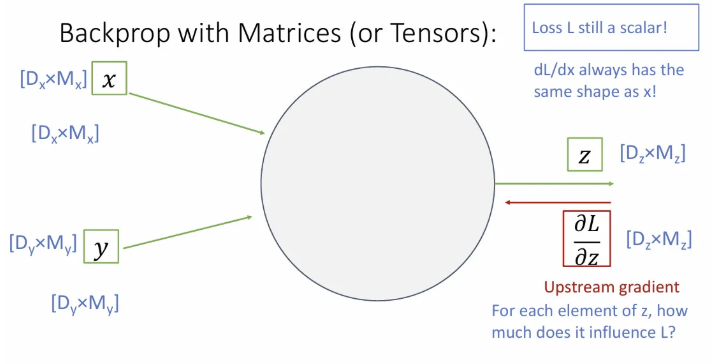
이제 한 단계 더 나아가 input, output 모두 행렬인 경우를 생각해보자. 여전히 Loss 은 scalar 값이고, 크기의 행렬 에 대한 의 미분값은 의 각 요소가 변함에 따른 의 변화를 의미하게 될 것이다.
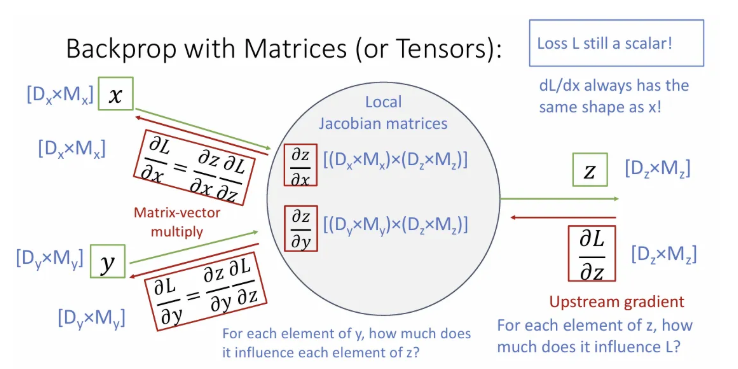
사실 위처럼 수식 그림만 봐서는 내 능지론 한계가 있다. 한 번 예시로 봐보자..
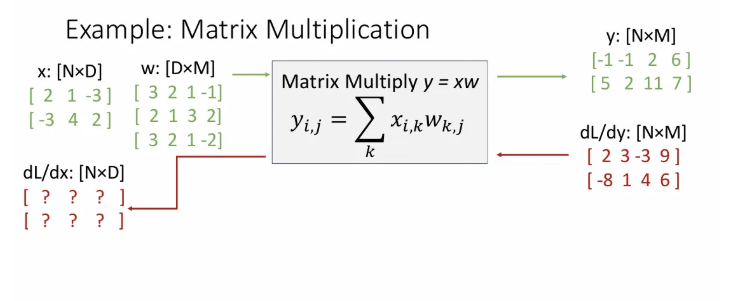
은 2, 는 3, 은 4 인 예시이다.
는 3차원의 row vector 2개를 갖는 행렬이고, 는 4차원의 row vector 3개를 가진 행렬, 는 4차원의 row vector 2개를 가진 행렬이다. 각 input에 대한 의 변화는 해당 input과 같은 차원인 것을 기억하면서 천천히 가보자.
forward pass에서 연산을 그대로 수행한 결과를 잘 갖고 있다.
만약 에 대한 의 변화량 행렬이 위와 같이 upstream gradient로 주어진다면 downstream gradient는 어떻게 구할까?
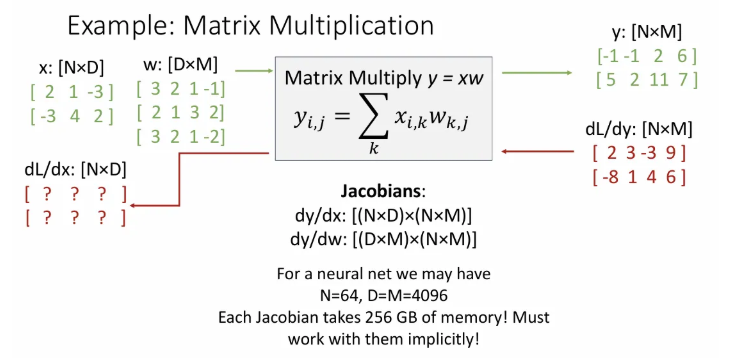
각 input에 대한 의 변화는 해당 input과 같은 차원이므로 는 2x3이 되고, 이와 곱해져서 2x4인 가 나오려면 는 [(2x3)(2x4)]이고, 는 [(3x4)(2x4)] 가 된다. 흔히 우리가 32x32x3 크기 이미지를 input으로 받고 batch size를 64로 설정한다면 한 번에 256GB의 gpu 메모리를 먹게 되기 때문에, implicit multiplication을 사용해야 한다.
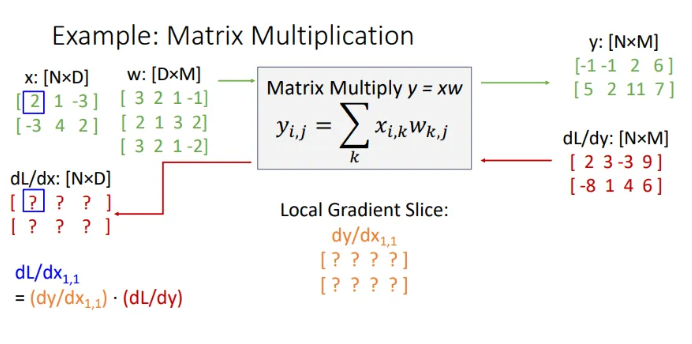
우선 먼저 부터 구해보면, 이는 와 같다. Upstream gradient는 이미 2인 것을 알고 있고, 는 이 변화함에 따라 의 각 요소가 어떻게 변하는지를 의미한다.
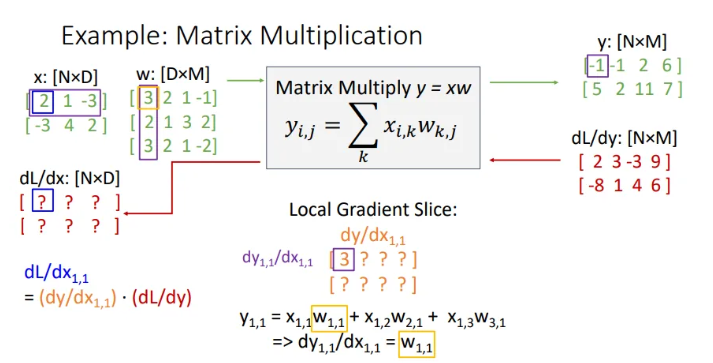
이제 의 첫번째 요소인 값이 무엇이 올 지 생각해보자. 일단 은 이고, 이를 에 대해 미분하면 이고, 이는 3이다.
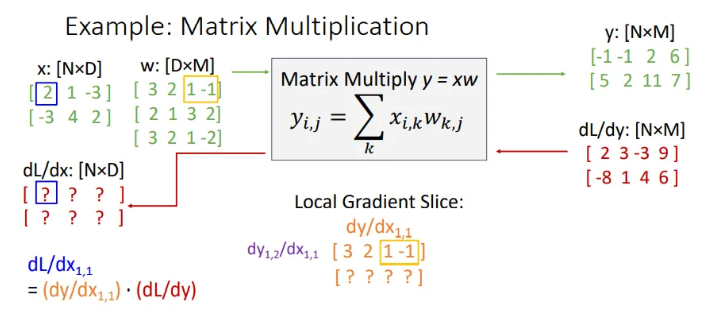
같은 방식으로 을 모두 채웠다. 모두 구하고 보니, local gradient의 첫 번째 row는 의 첫 번째 row와 똑같이 이루어져 있음을 확인할 수 있다. 그렇다면 두 번째 row는 어떻게 될까?
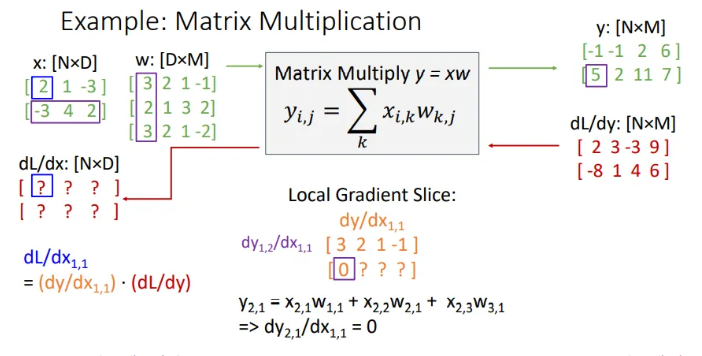
첫 번째 값부터 구해보자면, 이고, 이를 에 대해 미분하면 당연히 값은 0이 되고, 나머지 값들도 똑같이 0이 된다.
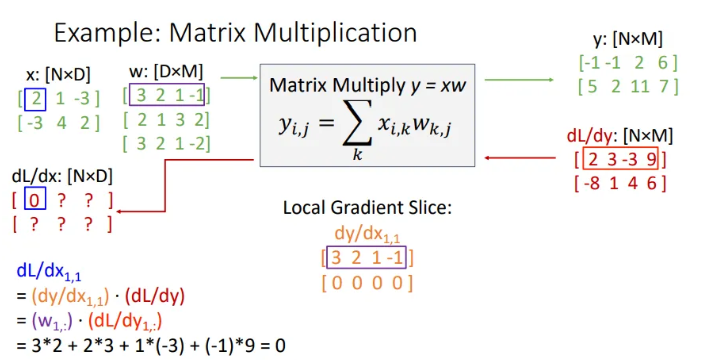
그렇다면 다시 돌아와서 은 사실상 와 를 곱한 것과 같게 되고, 이는 0이다. 어차피 의 첫 번째 row vector와 의 첫 번째 row vector를 내적한 결과인 scalar 값이 되는 것.
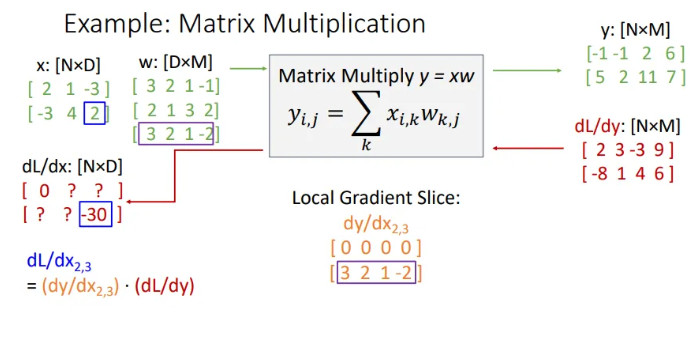
그렇다면 은? → 의 세 번째 row vector와 의 두 번째 row vector의 내적 값인 -30이 오게 된다.
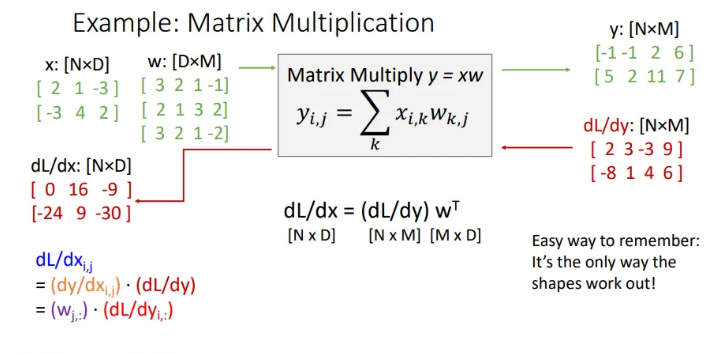
그렇게 식을 유도해보면, 는 로 표현 가능하다. 여기서 에 transpose를 취해주는 이유는, 우리가 조금 전 슬라이드에서 의 세 번째 row vector인 와 의 두 번째 row vector인 을 내적하는 연산을 생각해보면, 보통 는 행렬 연산으로 로 표현하는 것을 생각해보자.

마찬가지로 는 로 표현이 가능하다. 굳이 Jacobian 행렬을 만들지 않아도 위와같은 형태면 훨씬 적은 memory로 같은 계산을 할 수 있다.
Backpropagation: Another View

backprop을 생각하는 또 다른 관점은, 위와 같이 chain rule로 표현하는 것인데, 오른쪽→왼쪽으로 계산을 해보면, 이는 행렬 벡터 형태로 쭉 이어나갈 수 있다. 하지만 이는 input을 행렬로 받아서 최종 scalar 형태의 loss 을 계산할 때만 사용 가능. 이를 reverse-mode automatic differentiation이라고도 한다.

그렇다면 단일 scalar input을 받아서 vector output을 낼 때의 gradient를 얻고싶을땐? (순방향)
이렇게 forward mode로 생각해볼 수도 있다. 이는 머신러닝에서 쓰이는 아이디어는 아니고, 물리적 시뮬레이션에서 필요한 개념이라고 한다.

더 나아가서, 단순히 gradient와 Jacobian 행렬 뿐 아니라, 2차 도함수 및 Hessian 행렬에 적용도 가능하다.
References
유튜브 강의: https://www.youtube.com/watch?v=qcSEP17uKKY&list=PL5-TkQAfAZFbzxjBHtzdVCWE0Zbhomg7r&index=5
PDF: https://web.eecs.umich.edu/~justincj/slides/eecs498/FA2020/598_FA2020_lecture05.pdf