cs231n Lecture 4 | Introduction to Neural Networks 강의 정리

shyoon·2024년 12월 4일

cs231n 딥러닝 머신러닝 컴퓨터비전

cs231n

목록 보기

1/5

✍ 해당 시리즈 포스팅은 스탠포드 대학의 cs231n 강의 내용을 정리한 글입니다.

Computational Graphs

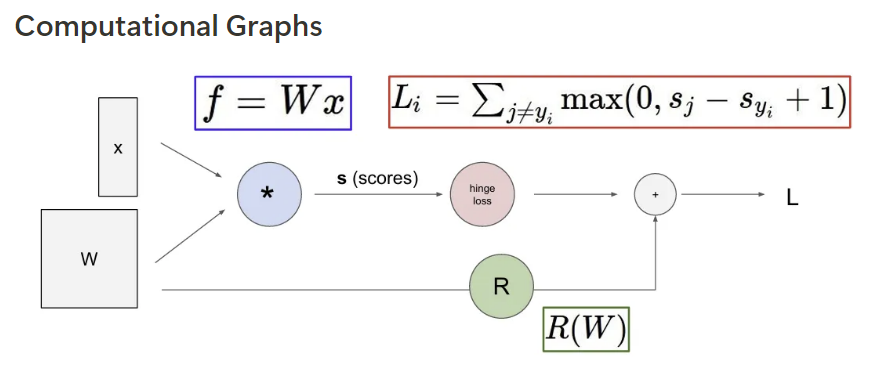
함수의 연산 과정을 node(계산 노드) 와 edge를 갖는 그래프 형태로 나타내는 것.

computational graph를 사용해서 함수를 표현하게 됨으로써 backpropagation 사용이 가능하다.

Backpropagation

gradient를 얻기 위해 computational graph 내부의 모든 변수에 대해 chain rule을 재귀적으로 사용

example

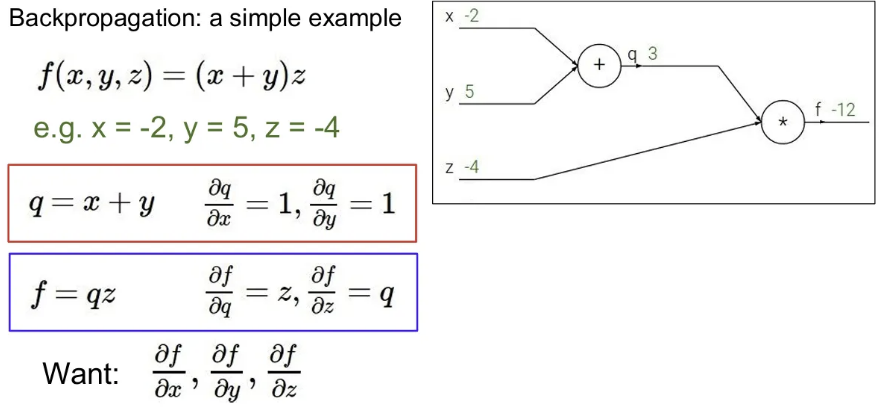
다음과 같이 $f(x,y,z) = (x+y)z$ 라는 식이 있을 때, 이를 computational graph로 표현하면 오른쪽과 같이 그릴 수 있다. 여기서 $x+y$ 를 $q$ , $qz$ 를 $f$ 라고 표현할 때, 그림에서 $x$ 와 $y$ 를 입력받아서 덧셈 연산하는 노드를 $q$ 로 표현이 가능하고, 이 $q$ 와 $z$ 를 입력으로 받아 곱셈을 수행하는 노드를 $f$ 로 표현 가능하다. 그리고 각 노드 별 매개변수에 대한 gradient 값은 위 그림 빨간 박스와 파란 박스대로 표현이 가능하다. (각 변수 $x$ 엔 $-2$ , $y$ 엔 $5$ , $z$ 엔 $-4$ 를 대입한다고 가정 )

이 때 우리가 $f$ 의 $x, y, z$ 각각에 대한 gradient를 찾기 원한다면,

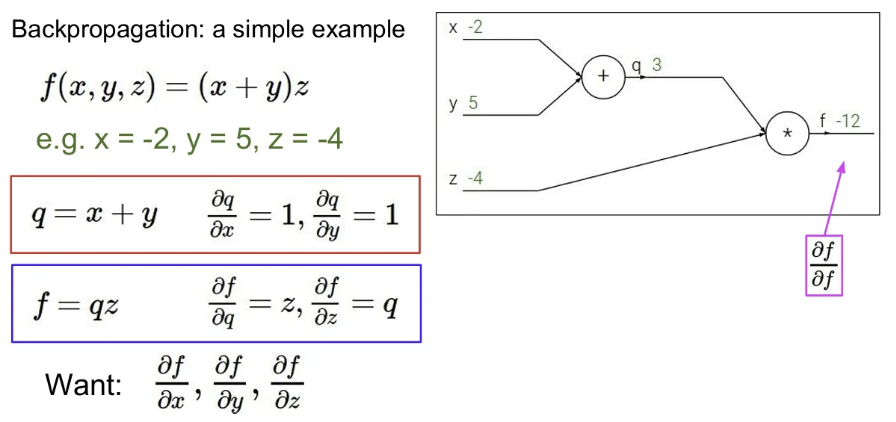
chain rule에 의해 computational graph의 맨 뒤에서부터 gradient 계산을 시작.

마지막 출력 $f$ 에 대한 gradient는 1. 이제 뒤로 계산 시작.

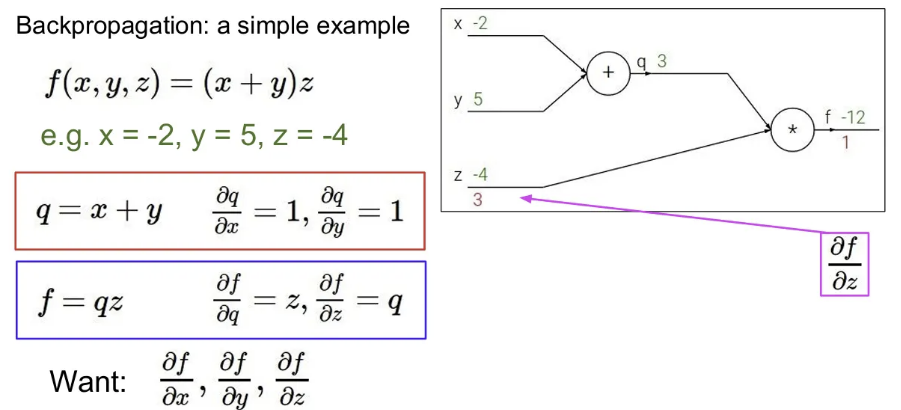
$z$ 에 대한 $f$ 의 미분 값은 $q$ 라는 것을 이미 알고있음. 이는 $x+y$ 값과 같고, 값을 대입해보면 3

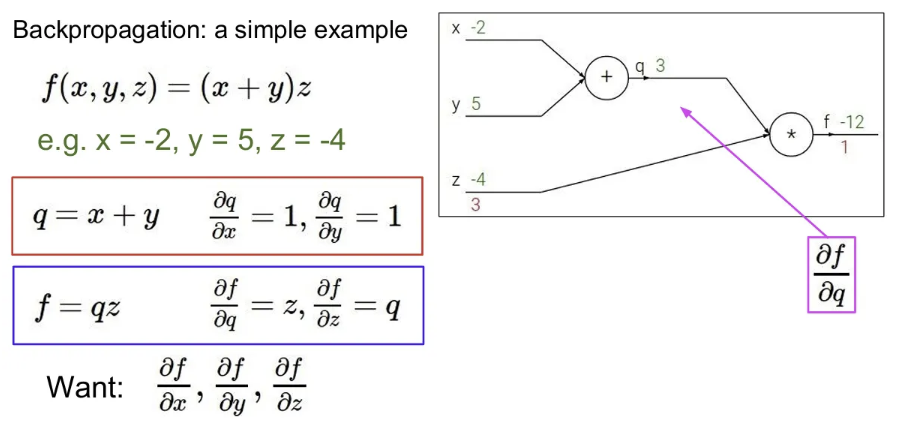
다음으로, $q$ 에 대한 $f$ 의 미분 값은 $z$ 인 것을 알고 있고, 이제 이를 활용해서 $x, y$ 에 대한 $f$ 의 미분 값을 계산할 수 있다. $y$ 는 $f$ 와 바로 연결되어 있진 않지만, chain rule을 통해서 아래와 같이 얻을 수 있다.

이는 다시 $z$ 로 나타낼 수 있어서, -4로 나타낼 수 있다. 같은 방식으로 $x$ 에 대한 $f$ 의 미분값 역시 $z$ 로 나타낼 수 있고, -4가 된다.

좀 전의 예제에서 벗어나, input으로 $x$ 와 $y$ 를 받는 $f$ 계산 노드에서 상류 input의 최종 결과값에 대한 gradient는 다음과 아래와 같이 chain rule을 통해 구할 수 있는 것.

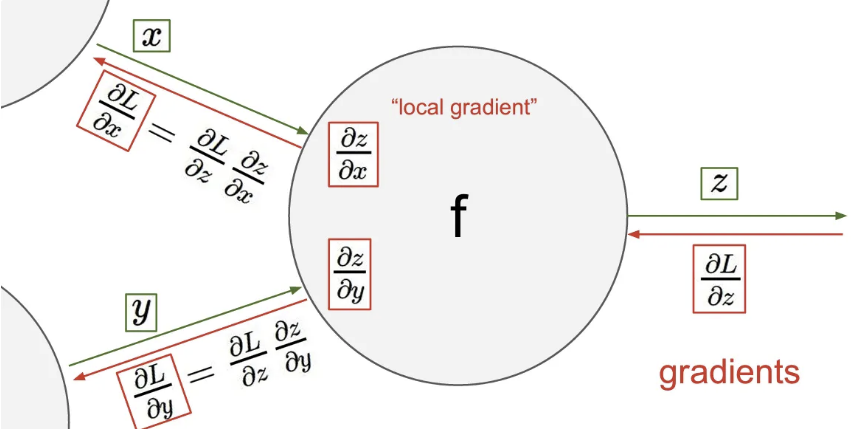
최종 결과인 $L$ 에 대한 $x$ 의 영향(미분값)은 $z$ 에 대한 $x$ 의 영향과 $L$ 에 대한 $z$ 의 영향을 곱한 것과 결과가 같다. 각 노드에서는 local gradient값을 가지고 있고, backpropagation을 통해서 최종 결과에 대한 그 local input의 gradient를 계산할 수 있게 된다.

+) max gate의 local gradient?

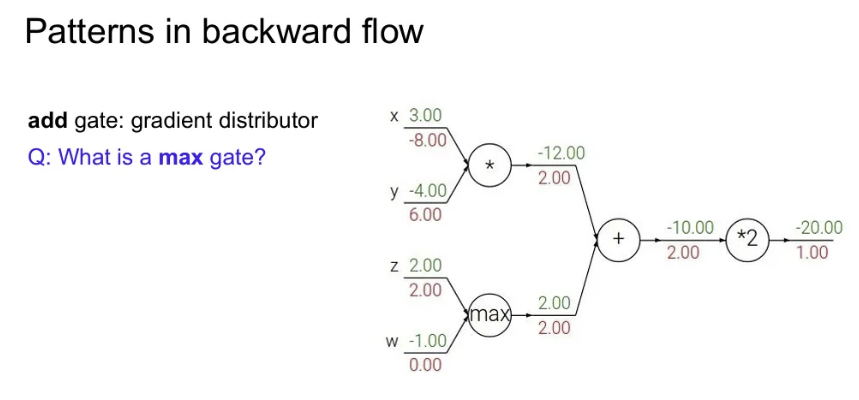
$z$ , $w$ 를 input으로 받을 때 max인 값에는 하류 gradient를 그대로 통과시키면 되고, 아닌 값에는 0을 전달

Vectorized operations

input에 벡터가 오게되면, gradient는 Jacobian 행렬 형태가 됨 (각 요소의 미분을 포함)

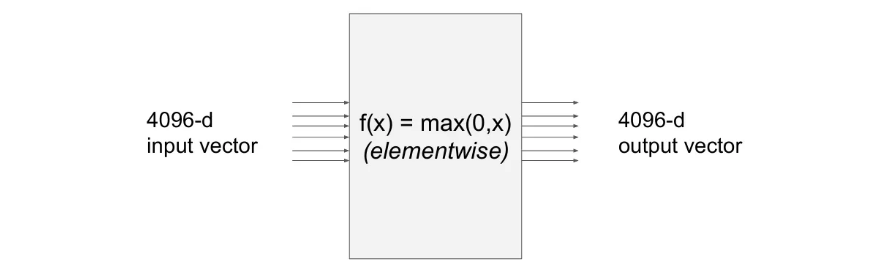
만약 input으로 4096 차원 벡터를 받아서 output도 똑같이 4096 차원 벡터를 내뱉는다면,

Jacobian 행렬의 size는 4096 X 4096.

만약 크기 100의 미니 배치를 사용했다면 409600 X 409600. → 너무 커짐

위 예시처럼 max 연산이었다면, 입력 벡터의 각 요소는 출력 벡터에서 자신과 같은 위치의 요소에만 영향을 미치므로, 대각 행렬 형태가 됨.

A vectorized example

아래처럼 행렬과 벡터의 연산으로 이루어지는 예시.

input 행렬 $W$ 와 벡터 $x$ 가 아래와 같이 주어졌을 때, 각 local 및 final output은 아래와 같다고 가정

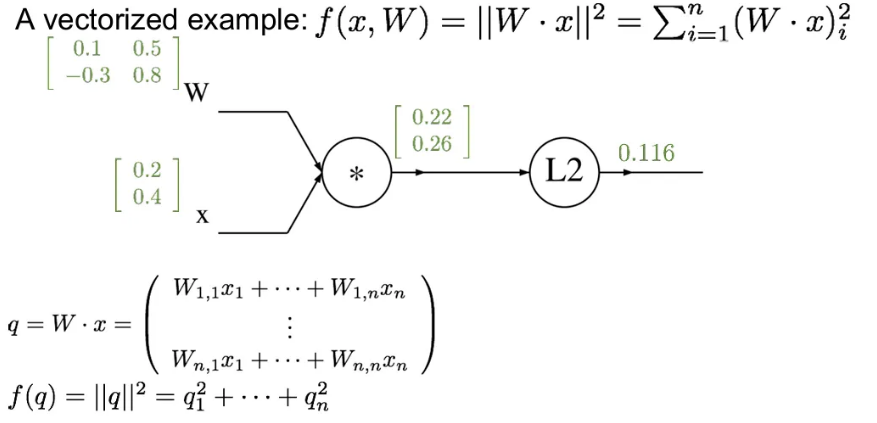
이제 backpropagation을 진행해보자.

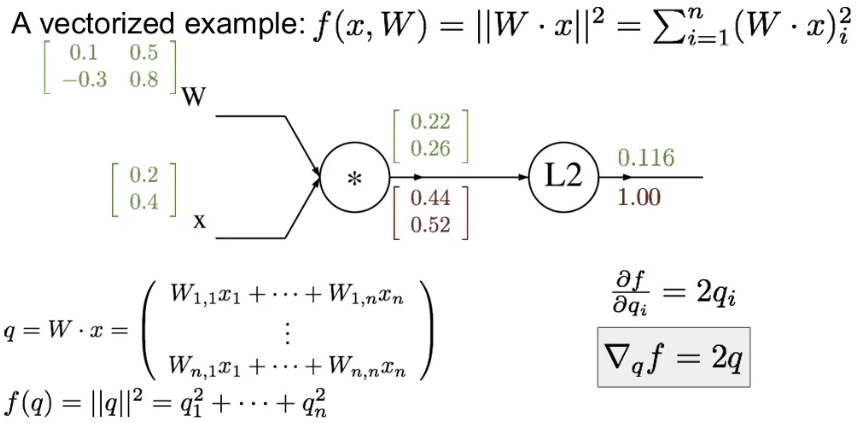
최종 $f$ 의 미분값인 1부터 시작해서, $q$ 에 대한 $f$ 의 gradient인 Jacobian 행의 각 요소는 $2q_i$ 를 가지게 됨.

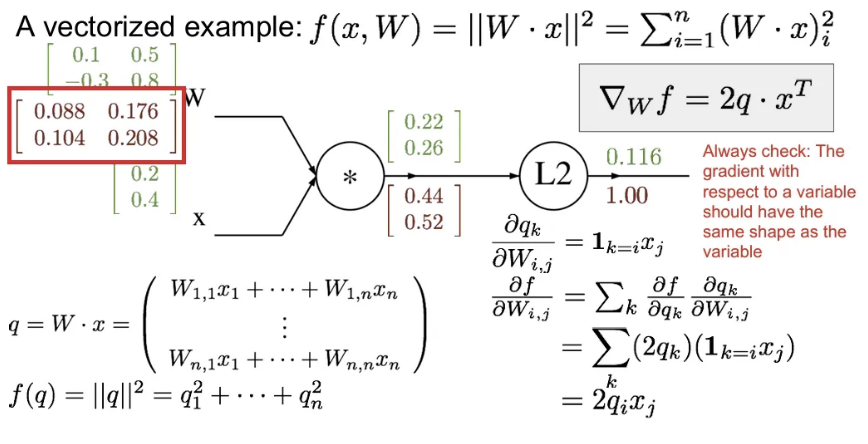
이제 $W$ 에 대한 $f$ 의 미분값을 구하기 위해서는 $q$ 의 $W$ 에 대한 local gradient를 먼저 구한 후, chain rule을 활용하면 됨. $W$ 의 각 $i,j$ 위치의 요소 별 연산을 수행하면 빨간 네모 칸의 Jacobian 행렬을 얻을 수 있다.

(※ 벡터의 gradient는 항상 원본 벡터의 사이즈와 같음)

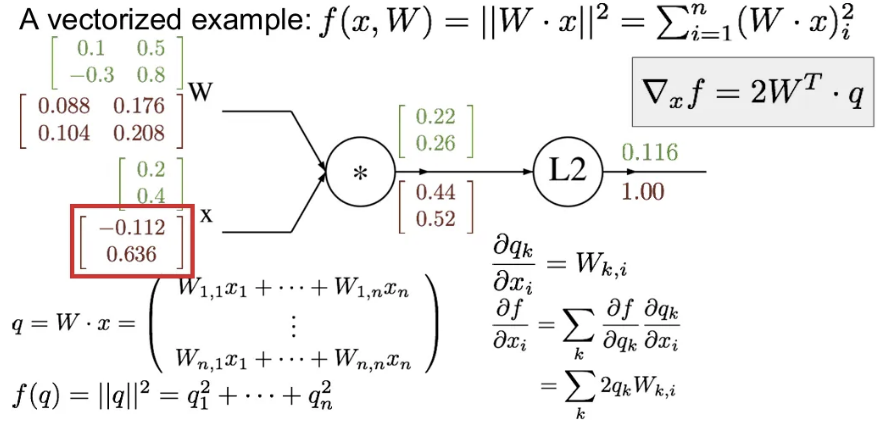
마찬가지로, $x$ 에 대한 $f$ 의 미분값을 구하려면 $q$ 의 $x$ 에 대한 local gradient를 구하고, chain rule을 적용하면 Jacobian 행렬을 얻을 수 있다.

Neural Networks

이전에 간단한 선형 변환식 $f = Wx$ 에 더하여, 이번엔 2층짜리 신경망 layer인 $f = W_2max(0, W_{1}x)$ 를 살펴 보자.

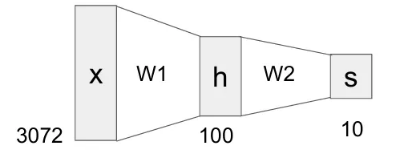
가장 먼저 $x$ 와 $W_1$ 을 행렬곱하여 중간값 $h$ 를 얻는다.
$max(0, W)$ 라는 비선형 함수(ReLU)를 적용한다.
$W_2$ 와 행렬곱하여 최종 출력값 $s$ 를 얻는다.

이 때 중간에 비선형 함수를 적용하는 이유? → 계속해서 선형 레이어만 쌓는다면 그 결과는 결국 어쨌든 선형 함수가 되기 때문

위 예시는 클래스가 10개인 CIFAR-10 데이터를 대상으로 간단한 2-layer neural network를 구성한 것. input으로는 3072차원의 벡터 $x$ 가 들어오고, (100, 3072)인 $W_1$ 와 행렬곱하여 100차원의 벡터 $h$ 를 중간과정에서 얻는다. 그 후 비선형 함수인 max 연산을 거친 후 $W_2$ 와 행렬곱하여 최종 10차원의 벡터 $s$ 를 얻게 된다. ( $W_2$ 는 $h$ 에 대한 score라고 생각)

이러한 layer들을 여러 번 쌓아나가는 것이 바로 Deep Neural Networks의 아이디어

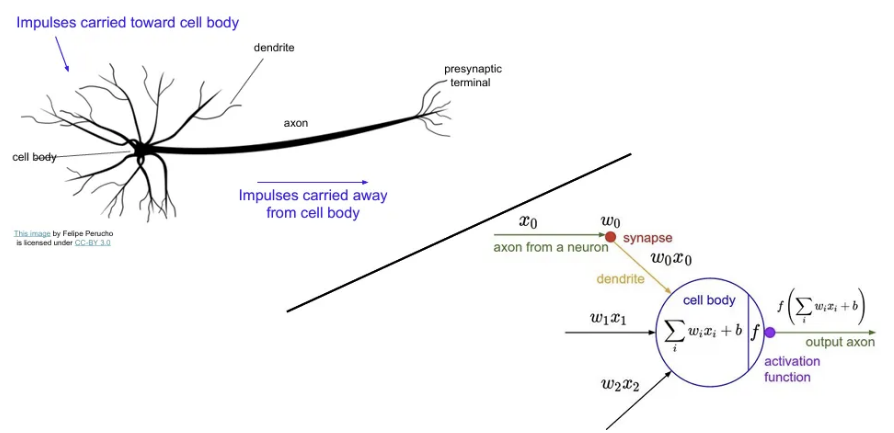
Computational graph의 형태는 실제 뉴런의 구조와 매우 유사하다. (물론 우리 뇌가 훨씬 더 복잡하긴 함)

Activation functions

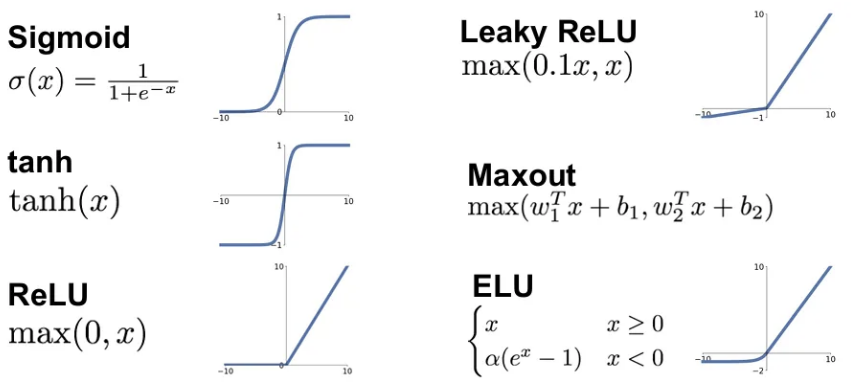
당연히 앞서 활용했던 ReLU(Rectified Linear Unit) 함수 말고도 훨씬 다양한 activation function들이 있다. (물론 위 함수들 외에도 매우 다양하고, 나중에 더 자세히 다뤄봄)

Neural Networks: Architectures

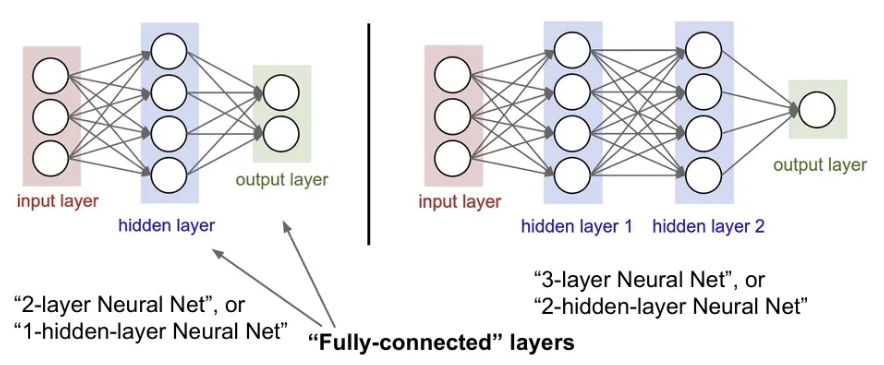
위 예시처럼 하나의 hidden layer(예시에서 $h$ )를 가지는 구조를 2-layer Neural Net 또는 1-hidden-layer Neural Net이라고 하고, hidden layer가 추가될수록 숫자는 증가한다. 그리고 위 그림들처럼 input과 weight의 완전한 행렬곱으로 이루어진 층을 Fully Connected Layers라고 한다.

Reference

shyoon

큰 사람이 되겠어요

다음 포스트