
✍ 해당 시리즈 포스팅은 스탠포드 대학의 cs231n 강의 내용을 정리한 글입니다.
Fully Connected Layer (Review)
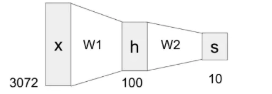
위 그림은 지난 시간 식을 그림으로 표현해 본 예시였다. input 벡터의 차원이 3072이고, 출력 벡터의 차원은 10이었다.
같은 크기의 input과 output으로 를 다시 한 번 그림으로 표현해보면 아래와 같다. input의 크기가 3072이었던 이유는 입력 이미지의 픽셀인 32 x 32 x 3 (가로, 세로, 채널)로 설정했던 것이다.
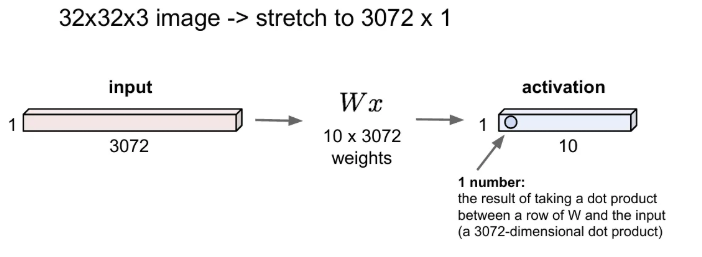
그리고 출력값은 10개가 나오고 있다. CIFAR-10 데이터셋의 클래스는 10가지이고, 각 10개의 출력값은 한 이미지를 input으로 받아서 각 10개 클래스에 해당 될 확률들을 가지게 된다.
Convolutional Layer
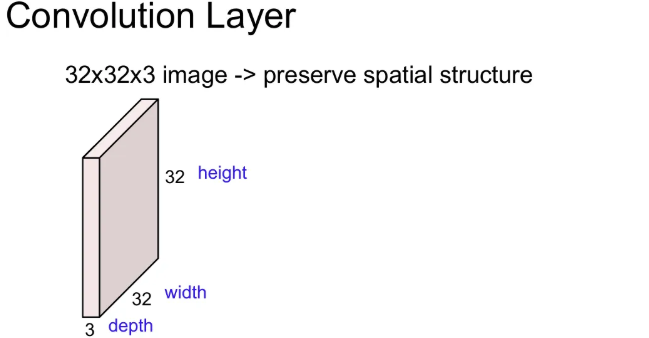
기존의 Fully Connected Layer에 이미지를 넣으려면, 해당 이미지를 길게 쭉 펴서 넣어야 했기에, 그 이미지의 공간 구조를 잃게 된다. 대신 Convolution Layer를 사용하게 되면, 이를 유지할 수 있다.
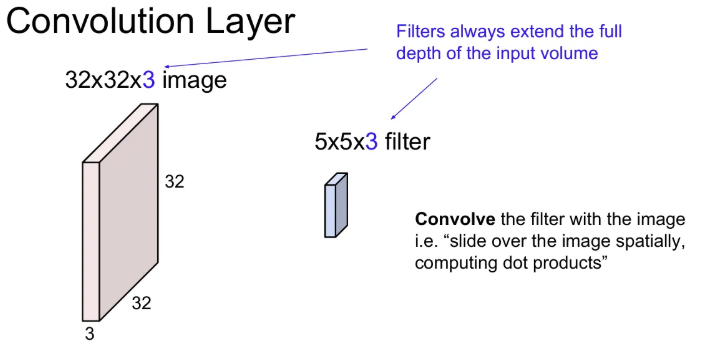
위 예시에서는 가중치 역할을 하는 필터를 5x5x3 크기를 활용했다. 이 필터로 이미지를 슬라이딩하면서 공간적으로 내적을 수행하게 된다.
※ 필터의 depth는 input volume의 depth만큼 확장된다.
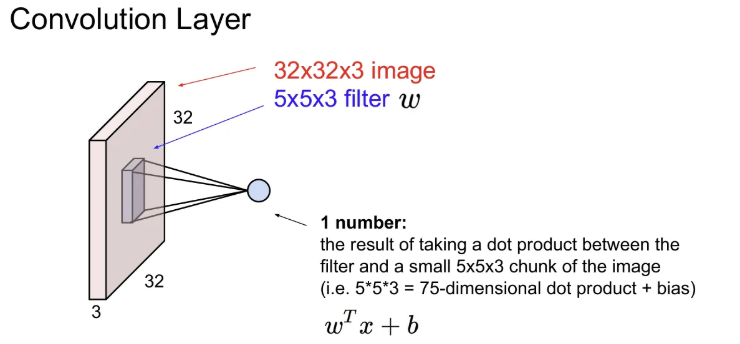
필터와 이미지의 특정 chunk(전체 이미지에서 슬라이딩하면서 정해짐)를 내적. 필터의 각 와 이에 해당하는 이미지의 픽셀을 곱해준다. (위 예시에서는 한 번에 5x5x3 번의 곱셈 연산과 하나의 bias term만큼의 연산이 수행)
(항상 이미지 chunk와 필터를 겹친 후 같은 위치 요소 별 곱한 후 더해주는 그림을 많이 봐서 깊게 생각은 안 해 봤었는데, 실제론 chunk와 필터 모두 펴준 후 내적 연산을 해야함)
실제로 신호 처리 분야에서의 convolution은 필터를 뒤집은 다음에 연산은 수행하지만, CNN의 convolution은 따로 뒤집진 않음. 사실 상 correlation을 하는 것.
이제 본격적으로 Convolution 과정을 살펴보자.
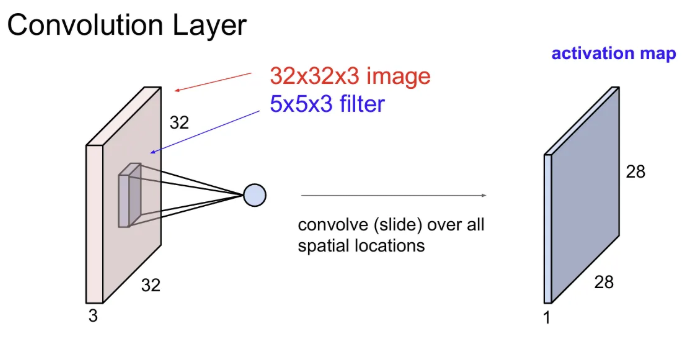
32x32x3 크기의 이미지에 첫 번째 5x5x3 필터로 convolution 연산을 수행한 결과, 오른쪽과 같은 28x28x1 크기의 하나의 activation map이 나온다(32→28로 줄어드는 이유는 뒤에서). 그리고 filter로 내적을 수행할 땐 depth에 관해서도 진행되므로, 한 필터에 대한 activation map에서 한 픽셀의 depth는 1이다.
이 때 여러개의 필터를 활용해서 각 필터마다 다른 특징을 추출하고, depth 방향으로 concat되는데, 만약 첫 번째 convolution layer에서 5x5x3 필터 6개가 있었다면 결과 depth는 몇일까?
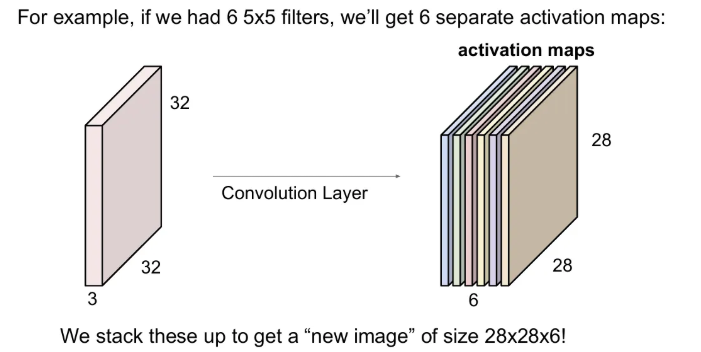
28x28 사이즈의 activation map이 6개가 합쳐져 depth 6의 결과가 나올 것이다.
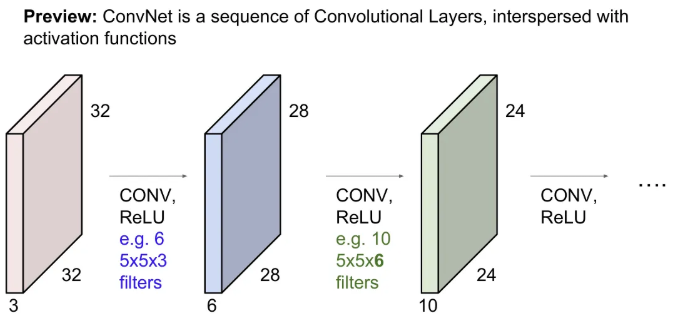
그렇게 convolution 연산을 해 준 후 보통 activation function을 적용해준다(pooling layer도 들어갈 수 있지만 위 예시에선 X). 위 그림대로면 원본 이미지에서 수행된 연산은 아래와 같겠다.
5x5x3 크기의 필터 6개로 convolution → ReLU → 5x5x6 크기의 필터 10개로 convolution → ReLU ~~
위와 같이 여러개의 layer를 쌓고나면 결국 각 필터들이 계층적으로 학습을 하게 됨
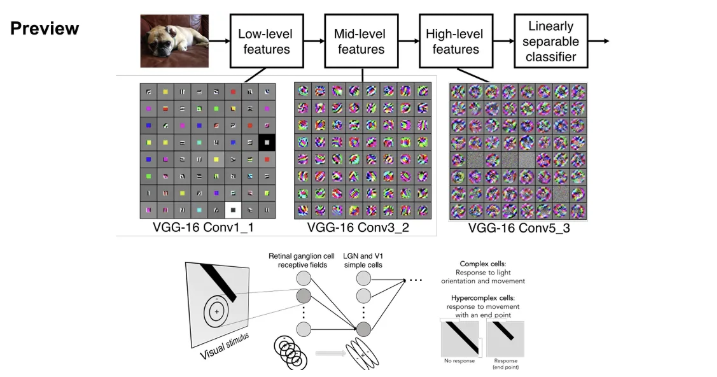
낮은 layer의 필터들은 low-level features(edge 등)를 학습하게 되고, 중간 layer의 필터들은 비교적 복잡한 특징(corner, blobs 등)을 학습한다. 그렇게 되면 layer가 높아질수록 필터는 좀 더 객체와 닮은 특징을 얻게된다.
네트워크 앞쪽에서는 단순한 것들을 처리하고 뒤로 갈수록 점점 더 복잡해지는 방식. 그리고 이 필터들의 학습은 계층적 구조를 설계한 후 역전파를 통해서 이루어진다.
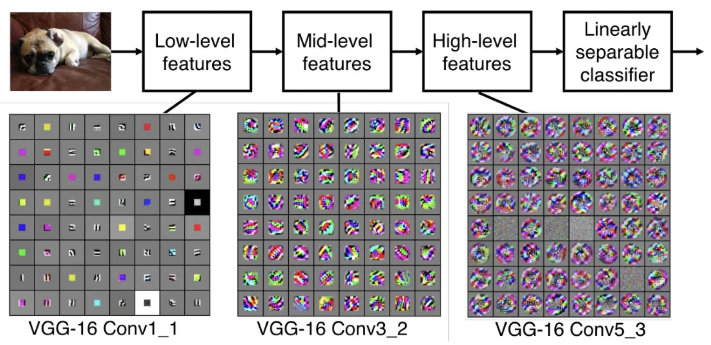
Conv1_1의 각 그리드 요소가 하나의 뉴런(필터) 라고 보면 되고, 시각화 된 모습은 이미지가 어떻게 생겨야 해당 뉴런(필터)의 활성을 최대화 시킬 수 있는 지를 나타낸다. 이미지가 뉴런과 비슷하게 생겼으면 큰 출력값을 가지게 됨.
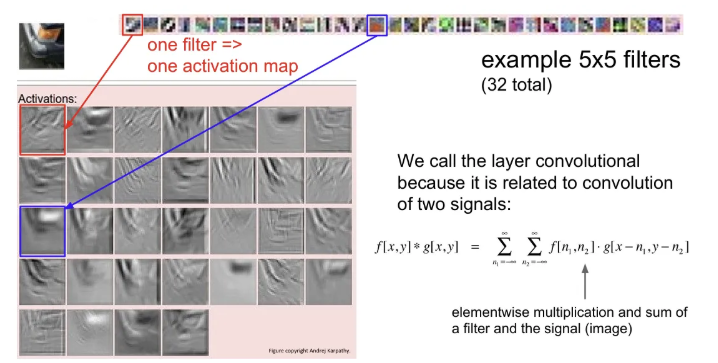
예시로, Input Image가 자동차의 한 부분이고, 32개의 학습된 필터로 Input image에 대한 각각의 activation map을 얻었다.
빨간 박스로 된 첫 번째 필터의 activation map을 보면 edge와 같은 요소들을 찾는다. 따라서 activation map의 결과는 Input image의 edge 부분에서 높은 activation을 갖는다.
파란 박스로 된 필터의 activation map은 주황색 요소들을 찾는 필터이기 때문에, activation map을 보면 Input image에서 주황색을 띠는 차량의 백라이트 부분에서 높은 activation을 보이고 있다.

보통 CNN의 구조는 Conv 후 non-linear activation을 반복하는데, 중간 중간 activation map의 크기를 조정하기 위한 Pooling layer도 들어가고, 마지막 layer에서는 최종 스코어를 계산하기 위해 Fully Connected Layer가 사용된다.
Spatial dimensions
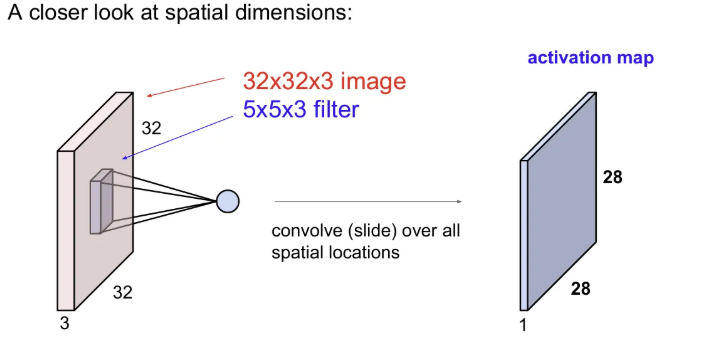
그래서 왜 32x32x3 이미지에 5x5x3 필터 하나를 적용한 결과 activation map의 크기는 28x28로 줄어들게 될까?

사이즈를 좀 줄여서, 7x7 input에 3x3 필터를 하나 적용해보면 sliding은 위와 같은 순서로 이루어지고, 각 박스에 해당하는 이미지의 일부와 필터값을 내적하면 하나의 값을 뽑게 된다(이 때 3x3 → 9, 크기로 늘린 후 내적 수행).
이렇게 한 줄 수행하고 나면 activation map의 첫 번째 행이 나오고, 가로 방향 sliding이 끝났다면, 아래로 한 칸 sliding 후 다시 왼쪽부터 sliding하면 결국 5x5 크기의 activation map이 나오게 된다.
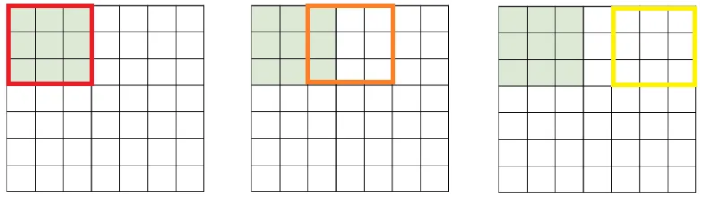
물론 sliding을 할 때 한 번에 몇 칸을 움직일 지 정해줄 수 있다. 이 칸을 stride라고 하고, stride를 1이 아닌 2로 설정하면 activation map의 결과는 3x3 크기가 된다. 즉, stride를 늘리면 activation map의 크기는 자연스레 줄어들게 된다.
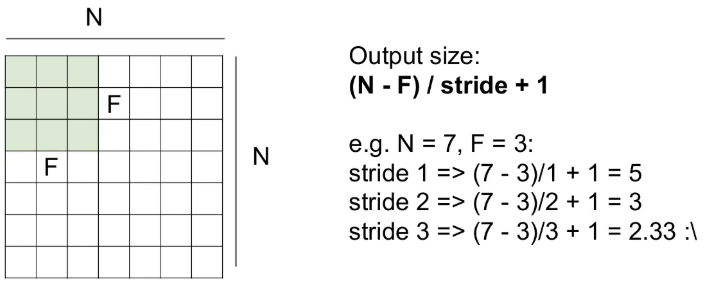
필터의 size와 stride 값에 따른 activation map의 크기에 대한 수식은 위와 같이 적용해볼 수 있다. 결과가 자연수가 아닌 값이 나오지 않도록 주의해야 한다.
Zero padding
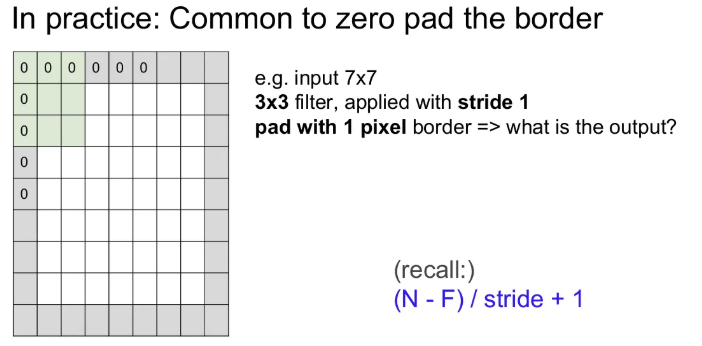
zero padding은 기존 이미지를 0값을 갖는 픽셀들로 감싸주는 것이다. 만약 zero padding을 해준 후 똑같이 크기 3x3 필터를 stride 1로 convolution 해주면 위 수식에서 (7 + 2 - 3) / 1 + 1 = 7로, 기존 input의 크기를 유지할 수 있다. 네트워크가 깊어질수록 activation map의 크기는 너 작아지게 되어 꼭 필요한 기법 중 하나이다.

stride 1일 때, Output의 size를 유지하려면 아래와 같이 padding을 주면 된다.
- 3x3 필터 → 1
- 5x5 필터 → 2
- 7x7 필터 → 3
Example

-
만약 input 이미지의 크기가 32x32x3 이고, 여기에 stride 1, pad 1로 10개의 5x5 크기 필터를 적용했을 때 결과의 크기 W x H x D 는?
- 우선 10개의 필터를 썼기 때문에 activation map은 10개가 만들어질 것이기 때문에 depth는 10이 될 것이므로, D는 10
- 각 activation map의 W, H는 가 되는데, N은 32+4이고, F는 5, stride 1을 대입하면 32이므로 32x32x10이 된다.
-
그렇다면 해당 layer의 파라미터 수는?
- 한 필터의 크기는 5x5x3 이고, 필터는 총 10개이다. 이라고 생각하고 끝날 수 있지만~
- 여기서 끝이 아니고, 각 5x5x3 필터의 가중치에는 하나의 bias term이 있기 때문에 이 된다.
Common settings

위 슬라이드는 Conv layer에서 흔히 많이 사용되는 setting을 정리한 것이니 참고
1x1 convolution
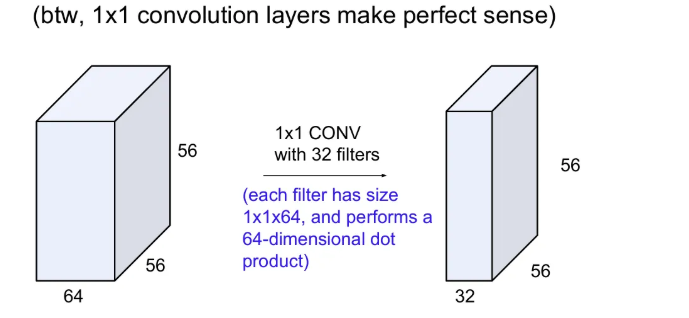
1x1 convolution도 가능한데, 얼핏 보면 똑같은거 아닌가? 하고 생각할 수도 있지만, input의 depth만큼의 내적 연산을 수행해서 하나의 activation map을 얻게 되고, 필터 수로 출력의 depth도 지정될 수 있다.
brain/neuron view
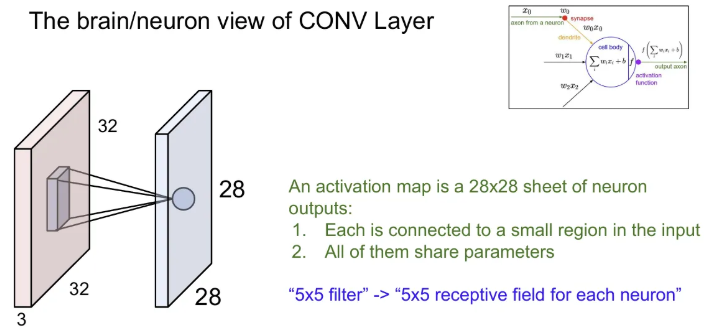
CNN에서 하나의 뉴런은 한 부분만 처리하고, 이런 뉴런들이 모여서 전체 이미지를 처리하게 됨 → 각 spatial structure를 유지한 채로 activation map을 만들게 된다.
※ 필터의 크기가 5x5라는 것은, 한 뉴런의 Receptive Field(한 뉴런이 한 번에 수용할 수 있는 영역)가 5x5 라는 것. 이 때, 각 뉴런 별 필터(가중)는 공유됨
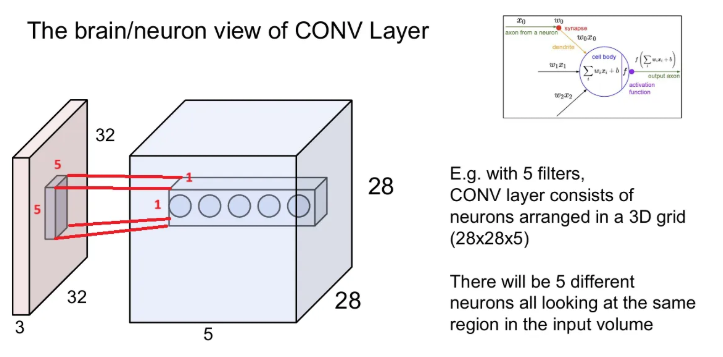
5x5x3 크기의 필터 5개로 conv를 수행했을 때 오른쪽과 같은 28x28x5인 3D grid가 되고, 파란색 map 안의 각 5가지 값들은 input의 같은 특정 5x5 지역에서 추출된 서로 다른 특징이 된다.
→ 각 필터는 이미지에서 같은 지역을 돌더라도 서로 다른 특징을 뽑아내는 것
Pooling layer
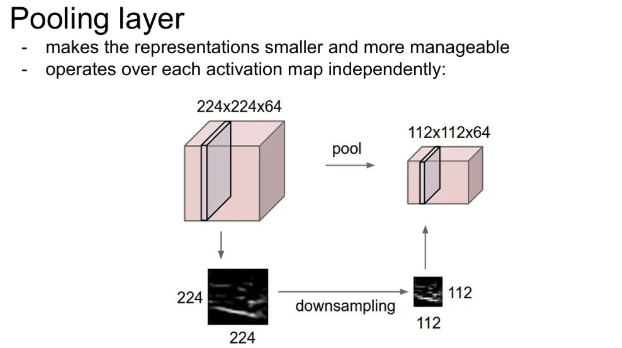
우리가 얻은 representations(activation maps)을 작게 Downsampling 해주는 것. 만약 224x224x64인 input이 있었다면, 114x114x64로 작게 만듦.
- 공간적으로 줄여줌.
- 이 때 depth에는 변화가 없다(activation map 수 변화 X)
- 주로 Max Pooling을 많이 사용
max pooling
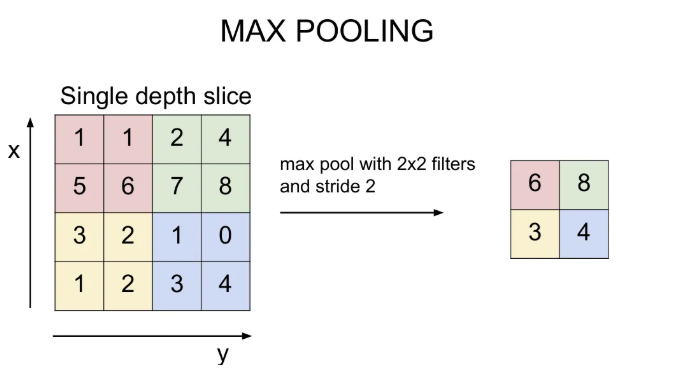
다음과 같이 2x2 필터, stride 2로 max pooling을 진행하면 각 공간 별 max 값을 뽑는다. 보통 필터 사이즈는 2x2나 3x3으로, stride는 2로 설정한다.
+) average pooling 대신 max pooling 사용하는 이유?
→ 우리가 activation map에서 다루는 값들은, 얼마나 이 뉴런이 활성화되었는지를 나타내는 것인데, max pooling은 그 지역이 어디든, 어떤 신호에 대해서 얼마나 그 필터가 활성화 되었는지를 알려준다.
FC layer in CNN architecture

마지막 Conv layer의 출력은 3차원 volume으로 이루어지게 되는데, 이를 전부 펴서 1차원 벡터로 만들어 FC layer의 input으로 사용하게 되면, Conv Net의 모든 출력을 연결하게 된다. 이 때는 굳이 공간적 구조를 신경 쓰지 않고, 전부 다 하나로 통합 시킨 후 얻은 score로 최종 inference를 한다.