데이터 군집화 - DBSCAN

✍DBSCAN이란?

데이터들의 밀도를 기반으로 군집을 형성하는 밀도 기반 알고리즘으로 각 개체의 반경 $\epsilon$ 내에 최소한의 이웃 개체가 존재한다면 하나의 군집으로 인식하는 방식

• 노이즈에 강건함
• 데이터 형태 무관
• 알고리즘의 복잡도가 작다

---

DBSCAN

$\epsilon :$ 이웃점 탐색 최대 반경
$minPts : $ 반경 내 최소한의 이웃점 개수 (자기 자신 포함)

• 각 개체를 Core, Border, Noise Points 세 가지 타입으로 지정
  • $\epsilon$ 반경 내에 $minPts$ 이상의 이웃점이 존재한다면 Core
  • $\epsilon$ 반경 내에 1이상, $minPts$ 미만의 이웃점이 존재한다면 Border
  • $\epsilon$ 반경 내에 이웃점이 하나도 존재하지 않으면 Noise

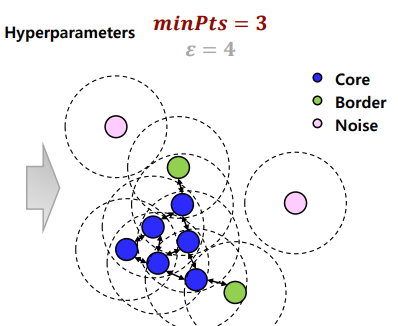
위 그림은 $\epsilon$을 4, $minPts$를 3로 설정했을 때의 예시 결과이다.
푸른색은 Core, 연두색은 Border, 분홍색은 Noise로 지정되고 있다.

위와 같이 다양한 모양의 군집에 적용 가능하다.

아래는 이 장점을 잘 보여주는 예시 코드이다.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.cluster import DBSCAN

# make_moons를 사용하여 반달 모양 데이터 생성
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)

# DBSCAN 알고리즘으로 군집화
dbscan = DBSCAN(eps=0.3, min_samples=5)
dbscan.fit(X)

# 군집 결과 확인
labels = dbscan.labels_
n_clusters = len(set(labels)) - (1 if -1 in labels else 0)  # 노이즈 데이터 제외한 군집 수

print(f"군집 수: {n_clusters}")

# 군집화 결과 시각화
colors = ['b', 'g', 'r', 'c', 'm', 'y', 'k']
for label in set(labels):
    if label == -1:
        # 노이즈 데이터는 검은색으로 표시
        color = 'k'
    else:
        color = colors[label % len(colors)]
    cluster_points = X[labels == label]
    plt.scatter(cluster_points[:, 0], cluster_points[:, 1], c=color, label=f'Cluster {label}')

plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('DBSCAN Clustering Example')
plt.legend()
plt.show()

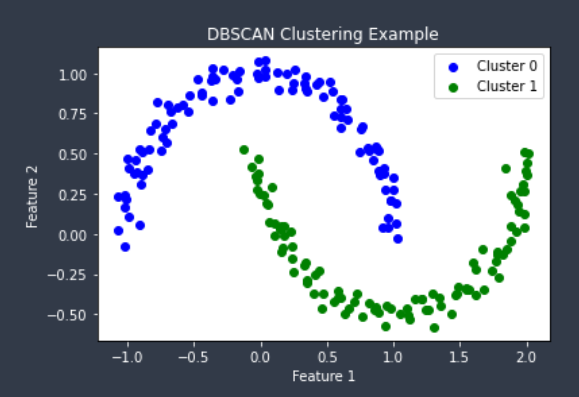
• 실행 결과
  
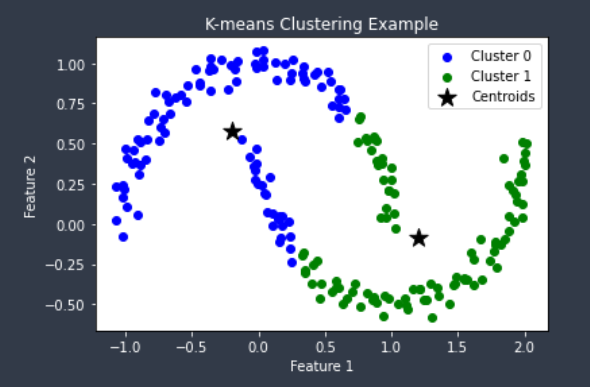
  그리고 아래는 같은 데이터셋을 K-Means를 이용하여 군집화 한 결과이다.
  
  위와 같이 지역적 패턴이 존재하는 군집을 판별하기 어려운 K-Means의 단점을 보완해주는 것을 확인할 수 있다.

---

한계점

• 다양한 수준의 밀도를 갖는 군집에 대해 강건하지 못하다.
• 하이퍼 파라미터($\epsilon$, $minPts$) 값에 예민하다. 이들을 적절히 설정하려면 도메인 지식이 필요하고 데이터 특성을 잘 알아야 한다.
• 고차원 데이터에 부적합하다(차원의 저주).

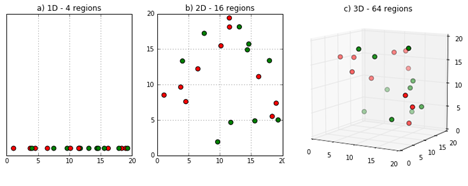
차원의 저주

⇨ 같은 양의 데이터가 고차원으로 이동할 수록 위와같이 채우지 못하는 공간이 증가하여 데이터 희소성이 발생하는 현상

---

References

• https://bcho.tistory.com/1205
• https://deepai.org/machine-learning-glossary-and-terms/curse-of-dimensionality