데이터 전처리 - 이상치 처리

✍ 이상치란?

관측된 데이터의 범위에서 많이 벗어난 아주 작거나 큰 값

이상치의 선형회귀모델에 대한 의미

• 다른 관측치와는 확연히 다른 데이터
• 데이터셋에서 제거했을 때 계산 결과를 눈에 띄게 변화시킬 수 있는 데이터 (영향점)
• 인접한 다른 외부 관측치로 인해 잘 감지되지 않음 (가면효과)
• 이상값의 영향에 의해 이상값이 아닌 관측값이 이상값으로 판정 (수렁효과)
• 이에 따라 강건한 중심위치와 공분산 행렬을 이용해야 함

---

이상치 탐색 방안

단변량 측면

• scatter plot
  

  하나의 x에 대한 y의 분포를 그리고, 직접 이상치를 색출함으로써 매우 직관적인 방법이다.

---

• Interquartile range(IQR)
  

  널리 이용되는 이상치 탐지 방법으로 데이터의 1사분위 수(Q1)와 3사분위수(Q3)의 차이인 IQR을 구하고, Q1 - IQR $\times$ 1.5를 하한선, Q3 + IQR $\times$ 1.5를 상한선으로 지정하고 그 밖의 값들을 이상치로 탐지하는 방법

# 예시 코드
import numpy as np
import pandas as pd

# 랜덤하게 50개의 데이터 생성
data = pd.Series(np.random.normal(loc=50, scale=10, size=50))

# 1사분위, 3사분위 구하기
q1 = data.quantile(0.25)
q3 = data.quantile(0.75)

# IQR 계산하기
iqr = q3 - q1

# 이상치 경계 계산하기
lower_bound = q1 - 1.5 * iqr
upper_bound = q3 + 1.5 * iqr

# 이상치 탐지하기
outliers = data[(data < lower_bound) | (data > upper_bound)]

print("이상치 경계값: ({}, {})".format(lower_bound, upper_bound))
print("이상치:", outliers.values)

• 실행 결과
  

• 특징
  • 데이터 분포의 영향을 받지 않는다.
  • 이상치를 검출하기 위한 기준이 명확하다.
  • 이상치를 감지하기 위한 구간 조정이 자유롭다.

---

• Z Score (Standard Score)
  

• z score는 표준편차를 이용해서 데이터가 평균으로부터 얼마나 떨어져 있는지를 나타내는 지표
• 일반적으로 z score가 $\pm3$ 인 경우 이상치로 판단

# 예시코드
import pandas as pd
import numpy as np

data = pd.Series(np.random.normal(0, 1, 1000)) # 평균이 0, 표준편차가 1인 정규분포 데이터 생성
threshold = 3 # z-score가 이 값 이상인 경우 이상치로 판단

outliers = data[abs((data - data.mean()) / data.std()) > threshold] # z-score로 이상치를 탐색
print(outliers)

• 실행 결과
  

---

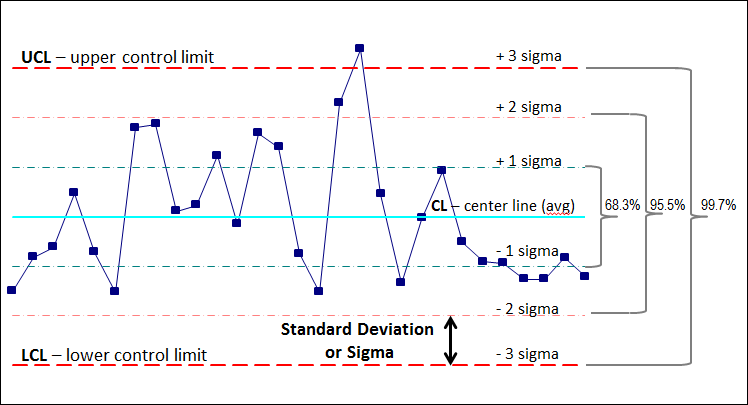
• UCL, LCL (Upper Control Limit, Lower Control Limit)

평균을 center로 하여
UCL = $\mu$ + (3$\sigma$),
LCL = $\mu$ - (3$\sigma$)
로 설정하고 UCL보다 높거나 LCL보다 낮으면 이상치로 간주하는 방법. 분포가 정규분포일 때만 사용 가능하다.

---

다변량 측면

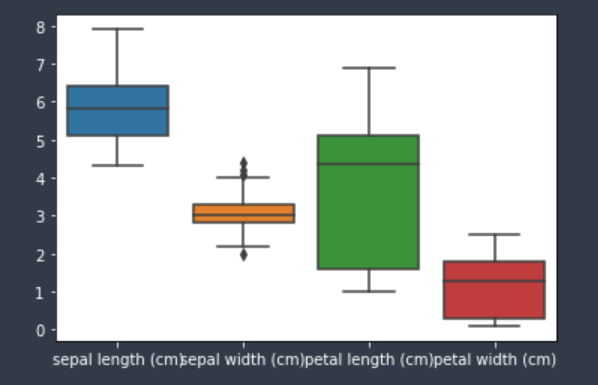
• Box plot
  

  IQR을 시각화 할 때 이용하기 좋은 그래프로 각 변수에 보이는 box의 천장은 Q3, 바닥은 Q1 값에 위치한다. 그 위 아래로 보이는 직선이 각각 Q1 - IQR*1.5 와 Q3 + IQR*1.5 안의 값들이고, 그 밖의 점으로 표시되는 값들이 이상치이다.

# 사이킷런의 Iris 데이터 셋 불러와서 이상치 탐색하는 예시 코드
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris

# Iris 데이터셋 불러오기
iris = load_iris()
iris_df = pd.DataFrame(iris.data, columns=iris.feature_names)

# 변수별 Boxplot 그리기
sns.boxplot(data=iris_df)
plt.show()

# 각 변수의 이상치를 IQR을 사용하여 찾기
for col in iris_df.columns:
    Q1 = iris_df[col].quantile(0.25)
    Q3 = iris_df[col].quantile(0.75)
    IQR = Q3 - Q1
    lower_outlier = Q1 - (IQR * 1.5)
    upper_outlier = Q3 + (IQR * 1.5)
    outliers = iris_df[(iris_df[col] < lower_outlier) | (iris_df[col] > upper_outlier)]
    
    print(f'\n{col}')
    print(f'IQR: {IQR}')
    print(f'Outliers: {outliers.index.values}')

• 실행 결과
  
  

---

• Cooks Distance
  

$D_i = \frac {\sum_{j=1}^n (\hat{Y}j - \hat{Y}{j(i)})^2} {p \times MSE}$

일 때,

$n$ : 관측치 수
$\hat{Y}_j$: 기본 회귀 모델의 $j$ 번째 예측값
$\hat{Y}_{j(i)}$ : $i$ 번째 관측치를 제거한 회귀 모델의 $j$ 번째 예측값
$p$ : 예측 변수의 개수
$MSE$ : 기본 회귀 모델의 평균 제곱 오차 (Mean Squared Error)

• 회귀 모델에서 특정 관측치를 제거한 후, 그 관측치와 다른 총 관측 값의 예측값 변화를 다룸으로써 해당 관측치가 해당 회귀 모델에 얼마나 영향을 주는 지 파악 가능
• 잔차와 레버리지를 동시에 고려
• $D_i$ > 1 이거나 $D_i$ > $4 \over n-p-1$ 일 때 이상치로 간주한다.