데이터 전처리 - 분포 변형

✍스케일링이란?

의도한 컨텍스트(context)에 맞추어 데이터를 변환하는 작업

🤷‍해주는 이유?

변수 1은 0~1 사이 값을 갖고, 변수 2는 0~100000까지의 값을 가진다면 변수 1의 영향이 작다고 판단 할 수도 있으므로 모든 변수의 분포를 같게 변형 해 줄 필요성이 있다.

주로 사용하는 방법은 표준화(Standardization), 정규화(Normalization) 등이 있다.

---

표준화(Standardization)

데이터가 평균으로부터 얼마만큼 떨어져 분포하는지 표현하는 변환

• Standard Scaler
  $z = {x_i - mean(x) \over stdev(x)}$
  • 중심 극한의 정리와 표준정규분포 이용
  • 관측된 변수의 모수 또는 표본평균의 확률함수가 정규분포에 근사할 것이라는 가정
  • 특성들의 평균을 0, 분산을 1로 바꿔줌
  • 이상치에 민감
  • 전처리 시 유용한 분석
    • 선형회귀
    • 로지스틱회귀
    • 선형판별분석

# 예시 코드
from sklearn.preprocessing import StandardScaler
import numpy as np

# 입력 데이터 예시
data = np.array([[1, 2, 3],
                 [4, 5, 6],
                 [7, 8, 9]])

# StandardScaler 객체 생성
scaler = StandardScaler()

# 데이터 스케일링
scaled_data = scaler.fit_transform(data)

# 스케일링된 데이터 출력
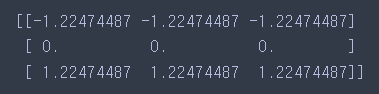
print(scaled_data)

• 실행 결과
  
  열(특성) 단위로 스케일링을 수행하기 때문에 행 단위로 스케일링을 진행하려면 Transpose를 취하고 스케일링 해야한다.

---

정규화(Normalization)

상대적 크기에 대한 영향을 줄이기 위한 변환

• MinMaxScaler
  $x'_i = {x_i - min(x) \over max(x) - min(x)}$
  • 가장 큰 값을 1로, 가장 작은 값을 0으로 스케일링
  • 따라서 모든 값은 [0, 1] 범위를 가짐
  • 이상치에 민감

# 예시 코드
from sklearn.preprocessing import MinMaxScaler
import numpy as np

# 입력 데이터 예시
data = np.array([[1, 2, 3],
                 [4, 5, 6],
                 [7, 8, 9]])

# MinMaxScaler 객체 생성
scaler = MinMaxScaler()

# 데이터 스케일링
scaled_data = scaler.fit_transform(data)

# 스케일링된 데이터 출력
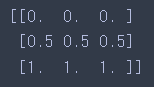
print(scaled_data)

• 실행 결과
  
  StandardScaler와 마찬가지로 열 단위로 스케일링을 수행한다.

• Robust Scaler

  $x'_i = {x_i - Q_1(x) \over Q_3(x) - Q_1(x)}$
  • 중앙값(median)과 사분위 값을 이용하여 스케일링
  • 이상치의 영향을 최소화 한 방법

# 예시 코드
from sklearn.preprocessing import RobustScaler
import numpy as np

# 입력 데이터 예시
data = np.array([[1, 2, 3],
                 [4, 5, 6],
                 [7, 8, 9],
                 [100, 200, 300]])

# RobustScaler 객체 생성
scaler = RobustScaler()

# 데이터 스케일링
scaled_data = scaler.fit_transform(data)

# 스케일링된 데이터 출력
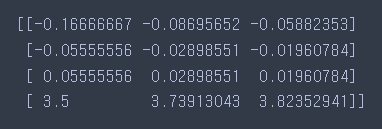
print(scaled_data)

• 실행 결과
  
  이상치에 덜 영향 받는 결과를 확인할 수 있으며, 다른 scaler와 마찬가지로 열 단위로 스케일링을 진행

• MaxAbs Scaler
  $x'_i = {x_i \over max(x)}$
  • 절댓값이 0~1 사이로 맵핑 되므로 각 값은 [-1, 1]로 조정
  • 이상치에 민감

# 예시 코드
from sklearn.preprocessing import MaxAbsScaler
import numpy as np

# 입력 데이터 예시
data = np.array([[1, 2, 3],
                 [4, 5, 6],
                 [7, 8, 9]])

# MaxAbsScaler 객체 생성
scaler = MaxAbsScaler()

# 데이터 스케일링
scaled_data = scaler.fit_transform(data)

# 스케일링된 데이터 출력
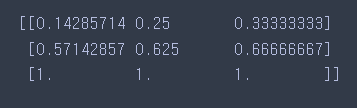
print(scaled_data)

• 실행 결과
  
  양수 데이터로만 이루어진 데이터 셋에서는 MinMaxScaler와 유사하게 적용되는 것을 확인할 수 있다.

---

기타 변환 방법

• 로그 변환(Log Transforamtion)

  $x'_i = log(x_i)$
  • 큰 수를 작은 수로 변환함으로써 계산 용이
  • 왜도와 첨도를 줄임으로써 분석에서 더 정확한 값을 얻을 수 있다.
  • 데이터 값 간 간격이 클 경우 좁혀 줄 수 있다.

# 예시 코드
import numpy as np

# 입력 데이터 예시
data = np.array([[1, 2, 3],
                 [4, 5, 6],
                 [7, 8, 9]])

# 로그 변환
transformed_data = np.log(data)

# 변환된 데이터 출력
print(transformed_data)

• 실행 결과
  

• 제곱근 변환(Square Root Transformation)
  $x'_i = a\sqrt {x_i+b+c}$
  • 치우친 분포 정규화
  • 변수간 비선형 상관성을 선형 상관성으로 변환
  • 선형 회귀에서 잔차의 이분산성 감소
  • 데이터의 특정 부분을 시각화하는 데 집중

# 예시 코드
import numpy as np

# 입력 데이터 예시
data = np.array([[1, 2, 3],
                 [4, 5, 6],
                 [7, 8, 9]])

# 제곱근 변환
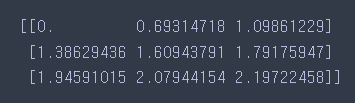
transformed_data = np.sqrt(data)

# 변환된 데이터 출력
print(transformed_data)

• 실행 결과
  
  제곱근을 이용하는 변환 방법이기 때문에 음수 값에는 적용 불가하며, 0 값도 미리 변환해 주어야 한다.

• Box-Cox Transformation

  $x'_i= \begin{cases} {x_i^\lambda - 1 \over \lambda},\ \ \ \ \ \ \ \;if\;\lambda \ne 0\\ log(x_i) , \ \ \ otherise \end{cases}$
  • $\lambda$ 값은 직접 지정해줄 수 있다.
  • 어떤 $\lambda$ 값을 사용하느냐에 따라 첨도 바뀌는 정도가 달라짐
  • 양수에만 적용 가능
  • $\lambda$ 값이 0일 경우 로그 변환, 1인 경우는 원래 데이터 이용과 같다.

# 예시 코드
from scipy import stats
import numpy as np

# 입력 데이터 예시
data = np.array([1, 2, 3, 4, 5])

# Box-Cox 변환
transformed_data, lambda_ = stats.boxcox(data)

# 변환된 데이터와 lambda 값 출력
print("Transformed data:", transformed_data)
print("Lambda value:", lambda_)

• 실행 결과
  
  입력 데이터는 1차원이어야 하며, boxcox() 함수는 일반적으로 최대우도추정을 이용하여 $\lambda$ 값을 설정해 준다.