✍앙상블이란?
하나의 모델이 아닌 여러개의 분류기를 생성하고 결합함으로써 단일 분류기보다 훨씬 강한 예측력을 보이는 기법
앙상블 배경
- No Free Lunch Theorem
어떠한 알고리즘도 모든 상황에서 모든 데이터에 대해 다른 알고리즘보다 우월하다는 결론을 내릴 수 없다는 이론
⇨ 문제의 목적, 데이터 형태 등을 종합적으로 고려하여 최적 의 알고리즘을 선택할 필요가 있다.
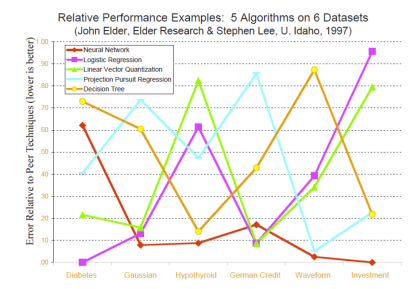
그림과 같이 데이터 셋마다 최적의 알고리즘은 모두 다르다.
수학적 배경
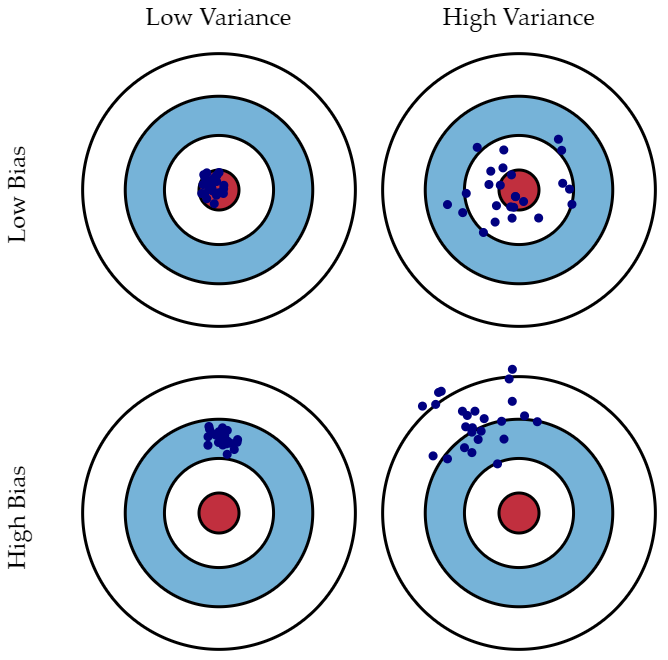
- Bias와 Variance
- (편향) : 모델의 예측 오차(추정 값과 실제 값의 차이)
- (분산) : 모델 예측의 편차(추정 값의 평균과 추정 값 간의 차이)
비유하자면 Bias를 낮추는 것은 영점 조절, Variance를 높이는 것은 자신이 보는 가운데를 잘 맞히는 실력을 증가시키는 것으로 보면 된다.
⇨ 둘 다 클수록 좋지 않기 때문에 낮출 필요가 있다.
X축을 모델 복잡도, Y축을 에러로 설정할 때, Bias와 Variance의 그래프를 그리면 위와 같이 둘은 Tradeoff 관계인 것을 확인할 수 있다. 따라서 두 합이 최소가 되는 지점이 되는 모델 복잡도를 이용해야한다.
그래프에서 확인할 수 있듯이, 모델 복잡도가 낮을수록 Bias는 커지고, 모델 복잡도가 높을수록 Variance가 커진다.
앙상블의 목표 및 효과
- 목표 : 다수의 모델을 학습하여 오류의 감소 추구
- 분산(Variance)의 감소에 의한 오류 감소 : 배깅(Bagging), 랜덤 포레스트(Random Forest) 이용
- 편향(Bias)의 감소에 의한 오류 감소 : 부스팅(Boosting) 이용
- 효과
- 이론적으로 각 모델이 서로 독립이라는 가정 하 M개의 개별 모델 결합한 앙상블의 경우 오류는 각 모델의 평균 오류의 1/M 수준으로 감소
- 현실적으론 당연히 1/M 수준까지 줄어들지는 않으나, 개별 모델들의 평균치보다는 항상 우수하거나 같은 성능을 나타냄
앙상블의 다양성 확보 방법
- 동일한 모델을 여러 개 사용하는 것은 아무런 효과가 없음
- 개별 모델은 서로 적절하게 달라야 앙상블의 효과를 볼 수 있다.
- 개별적으로는 어느정도 좋은 성능을 가지면서, 앙상블 내에서 각각의 모델이 서로 다양한 형태를 나타내는 것이 이상적
앙상블 기법 종류
- 배깅 (Bagging)
- 부스팅 (Boosting)
- 보팅 (Voting)
각 기법들의 자세한 내용들은 다음 포스팅에서!