시간 복잡도 (Time complexity)

시간 복잡도란?

알고리즘을 구상할때 원하는 결과 도출을 목표로 하는 것을 1순위 목표로 설정하되
효율적으로 코드를 구성하였는지도 항상 염두할 것
-> 효율적으로 코드를 구성한다는 것은 시간복잡도를 최소화한다는 것과 동일 의미

시간 복잡도를 최소화 할 수 있는 방법

입력이 증가했을때 연산횟수도 똑같이 증가하게 된다. 이때, 증가하는 연산 시간의 비율을 최소화 시킬 수 있어야 한다.

ex

• i <- 1 to n
  sum += i;
• sum = (n-1)*n/2

위 두 코드의 시간복잡도는 각각 O(n) O(1)

시간 복잡도의 표현 방법

• Big Oh

  최악의 경우 / 상한 점근
  $f(n) = 2n^2 + 3n + 1$
  
  임의의 점 $n_0$ 에서 $g(n)>=f(n)$ 을 만족시키는 임의의 상수 $c$가 하나라도 존재한다면

  $f(n) = O(n^2)$ 이다.
  $f(n) != O(n*logn), O(logn)$
  * 이때 $g(n) = c*n^2$

• Big Omega

  최선의 경우 / 하한 점금
  $f(n) = Ω(n^2)$ 이고, 아래와 같이 나타낼 수도 있다.

  $f(n) = Ω(n*logn), Ω(logn)$

  $g(n)<=f(n)$ 를 만족한다면 모든 $g(n)$ 에 대해 $Ω(g(n))$ 이 만족한다.
  

• Big Theta

  Big Oh 와 Big Omega 표현이 동일할때 사용
  최악과 최선 경우의 평균을 나타내는 시간복잡도

Big O 표기법의 종류

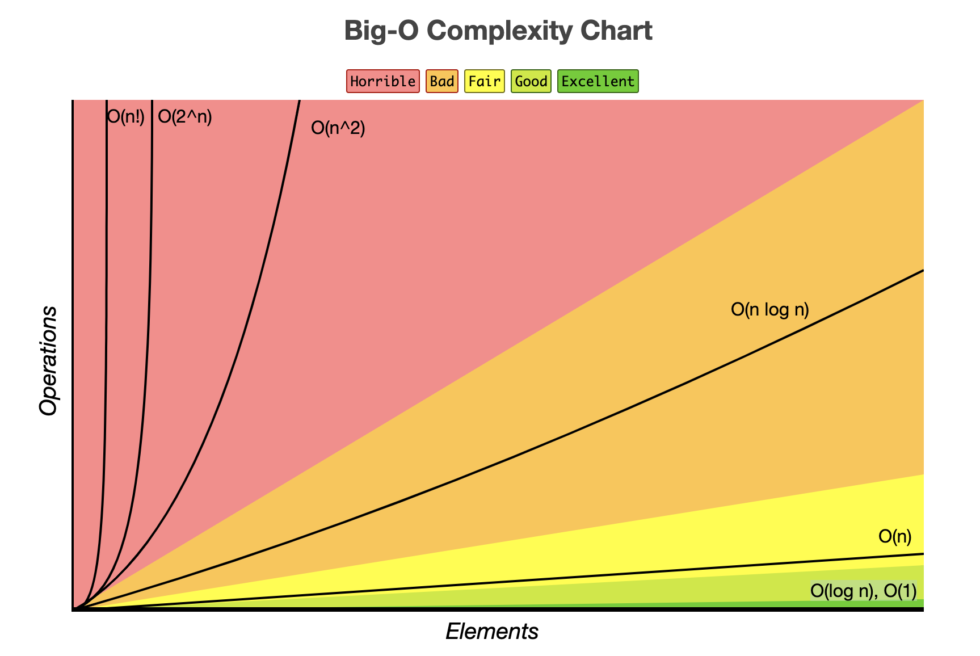
• O(1)

  상수시간 복잡도
  가장 효율적이고 입력의 크기와 관계없이 항상 동일한 수행시간을 갖는다
  ex) pop, push 알고리즘

• O(log n)

  로그시간 복잡도

ex) 이진탐색 알고리즘
n개의 데이터 값 중 특정 값을 찾는 이진탐색에서
k번 이진탐색을 진행했을 때 남게될 데이터의 갯수는
$N*(1/2)^k$
즉 $N*(1/2)^k=1$ 을 만족하는 $k=log_2(n)$

• O(n)

  선형시간 복잡도
  ex) for문

• O(n^2)

  2차시간 복잡도
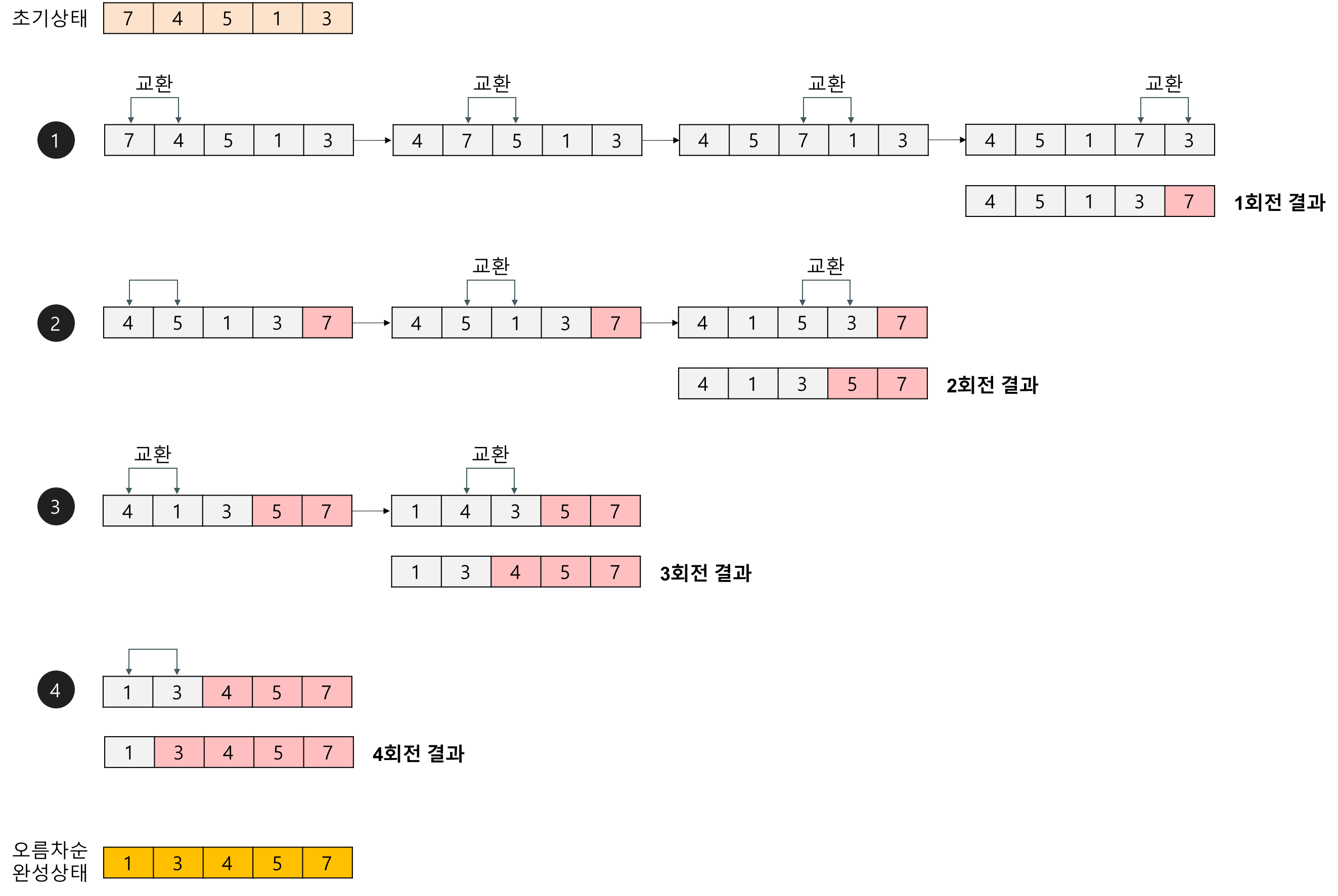
  ex) 이중 for문, 버블정렬, 선택정렬

ex) 버블정렬
인접한 두 항을 비교하며 정렬하는 알고리즘

첫 n-1번의 시행에 가장 큰 숫자가 맨 뒤로 이동하고
둘 n-2번의 시행..

ex) 선택정렬

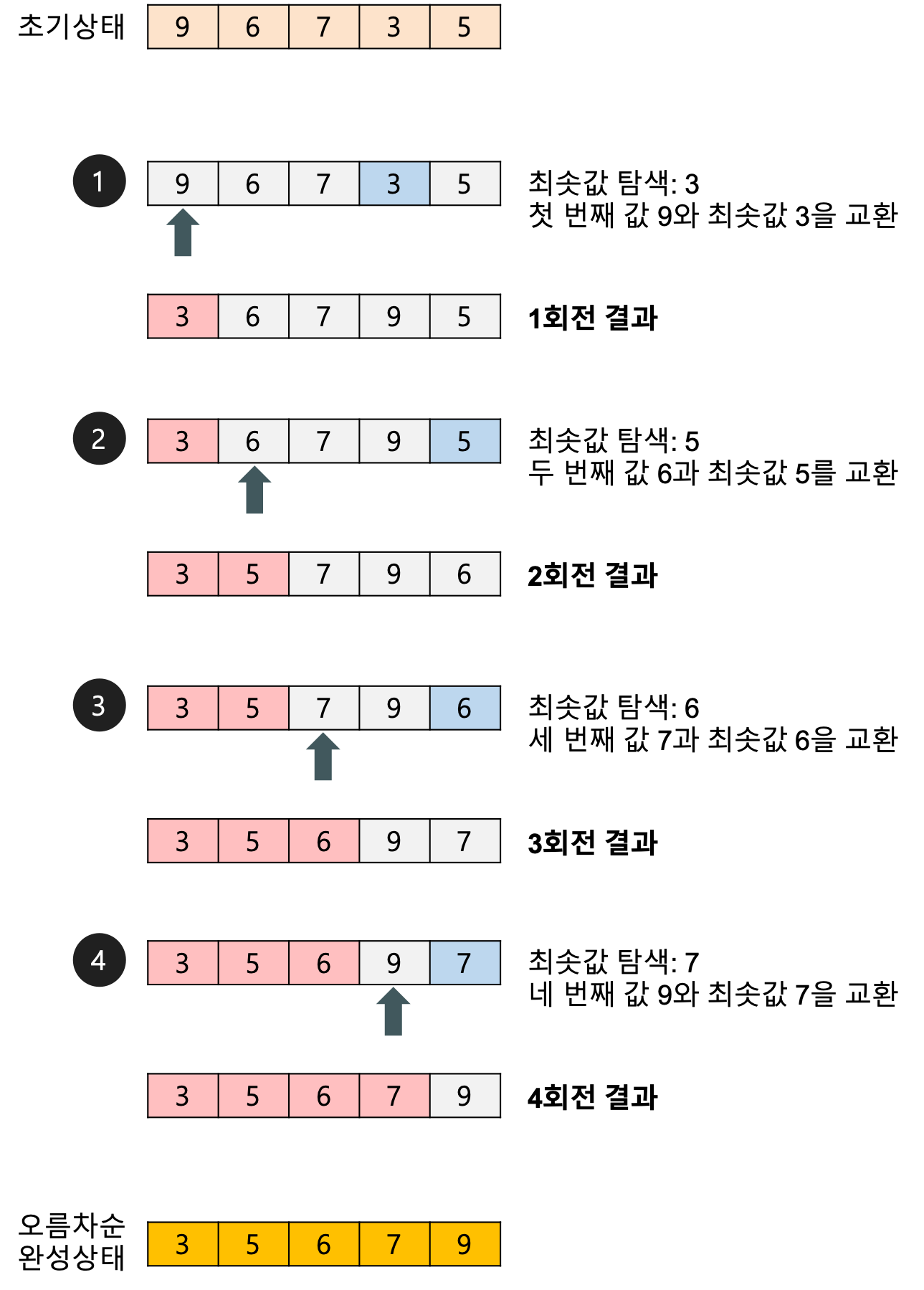
첫번째 시행에 1번 데이터와 이외 데이터들과 비교해 가장 작은 값을 찾아 자리 바꾸기
두번째 시행부터는 2번 위치에 데이터와 이외 데이터들 비교

#include <stdio.h>
#define SWAP(x,y,temp) ( (temp)=(x), (x)=(y), (y)=(temp) )
#define MAX 5;
//선택정렬 가장 작은 값 이동시키기

void selection_sort(int list[], int n){
	int min, temp;
	for (int i= 0; i<n-1; i++){
		min = i;
		for (int j=i+1; j<n; j++){
			if (list[j]<list[min]){
				min = j;
			}
		}
		if (min != i){
			SWAP(list[i],list[min],temp);
		}
	}
}

void bubble_sort(int list[], int n){
	int i,j,temp;
	for (i=n-1; i>0; i--){
		for (j=0; j<i; j++){
			if (list[j]>list[j+1]){
				SWAP(list[j],list[j+1],temp);
			}
		}
	}
}