정렬

• 데이터를 탐색하기 위함.
  
  컴퓨터는 데이터베이스 같은 경우 이론상 무한개의 데이터를 처리할 수 있어야함.
  
  정렬되어 있지 않은 데이터의 경우 순차탐색 알고리즘 밖에 사용할 수 없다.
  
  정렬된 데이터의 경우 이진탐색 을 사용할 수 있다.
  -> 알고리즘 문제를 풀 때 $n*log(n)$ 보다 빠른 방법이 없다고 판단되면 일단 데이터 정렬을 가정하고 문제를 풀어도 무방할 정도로 데이터의 정렬은 중요하다.
  -> 이진탐색보다 발전한 비례탐색 알고리즘도 존재

• 데이터의 값을 서로 비교해서 순서에 맞게 자리를 바꾸는 정렬을 비교정렬 이라고 하는데,
  온갖 수단과 방법을 동원해서 현재 비교정렬은 $nlog_2(n)$ 의 시간복잡도가 최선임이 증명되었다.

• 하지만 하드웨어 측면에서의 개입으로 더 느려야 할 알고리즘이 더 빠르다든가 하는 현상이 발생하기도 한다.
  
  ex) 정렬된 자료를 퀵 정렬 vs 다른 정렬 알고리즘

---

안정 정렬과 불안정 정렬

• 안정 정렬 (stable sort) 은 중복된 값을 입력 순서와 동일하게 정렬한다.
  
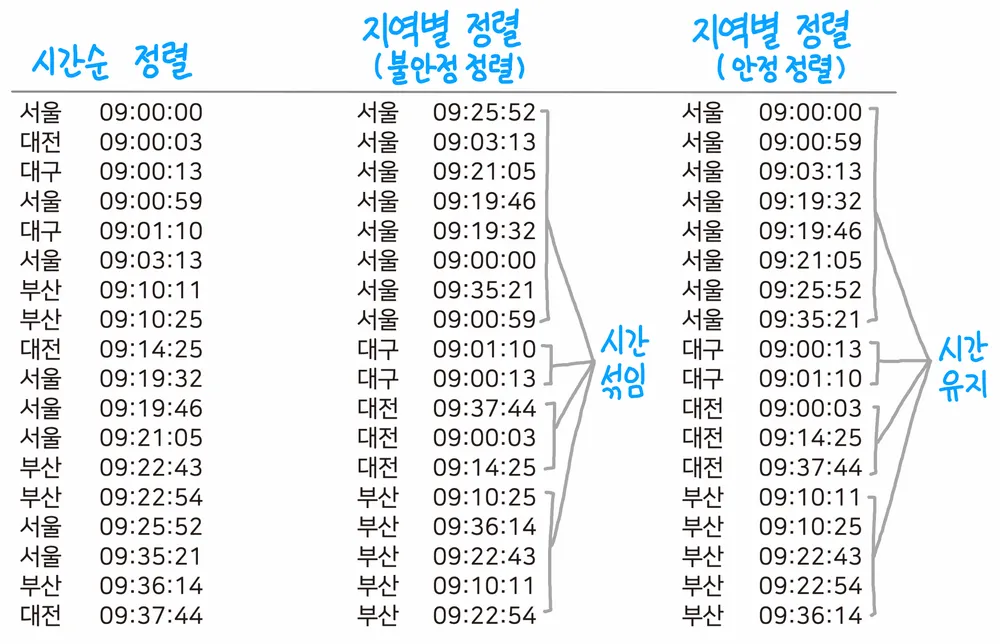
  한 눈에 봐도 안정 정렬이 불안정 정렬보다 유용함
  대표적으로 병합정렬 (merge sort) , 버블 정렬 등이 안정 정렬이고,
  퀵 정렬 등이 불안정 정렬이다.
  -> 최고의 알고리즘이라 평가 받는 퀵정렬이 입력이 어떻느냐에 따라 최악이 될 수도 있다.

---

정렬의 종류 (버블, 선택, 삽입)

시간 복잡도가 $log(n^2)$

• 버블 정렬

  n개의 입력이 존재할 때,
  1번 원소를 2번 원소와 비교해 정렬, 2번 원소를 3번 원소와 비교해 정렬, ...
  위 과정을 n번 반복해서 정렬
  
  대단히 비효율 적이라서 웬만하면 쓰지 말 것..

버블정렬 코드

void Bubble_Sort(int arr[], int len) {
  int i, j, tmp;
  for (i = 0; i < len - 1; ++i) {
    for (j = 0; j < len - i - 1; ++j) {
      if (arr[j] > arr[j + 1]) {
        tmp = arr[j];
        arr[j] = arr[j+1];
        arr[j+1] = tmp;
      }
    }
  }
}

• 선택 정렬

  첫 번째 시행에 1번 원소를 기준으로 나머지와 비교해 가장 값이 작은 원소를 찾아 1번 원소와 자리 교환
  두 번째 시행에 2번 원소를 기준으로 나머지와 비교해 2번째로 작은 원소 찾아 2번 원소와 자리 교환
  ...
  
  입력값이 어떻게 정렬되어있는지와 관계없이 오롯이 입력값의 갯수에만 연산 속도가 좌우된다.
  -> $n(n-1)/2$
  버블 정렬보다 두 배 정도 빠르다.

선택 정렬 코드

  void selection_sort(int list[], int n){
	int min, temp;
	for (int i= 0; i<n-1; i++){
		min = i;
		for (int j=i+1; j<n; j++){
			if (list[j]<list[min]){
				min = j;
			}
		}
		if (min != i){
			SWAP(list[i],list[min],temp);
		}
	}
}

• 삽입 정렬

  k번째 원소를 1~k-1 번째 원소와 비교해 적절한 위치에 끼워넣고 그 뒤 원소들을 한 칸씩 뒤로 밀어내는 방식
  $O(n^2)$ 중 빠른 편이지만, 자료구조에 따라서 뒤로 밀어내는 원소의 갯수가 무한정에 가까워질 수도 있어서 값이 작은 데이터가 뒤쪽에 몰려 있으면 비효율적이다.
  
  이미 정렬되어 있는 자료구조에 삽입/제거하는 경우 최고의 정렬 알고리즘
  배열이 작을 경우에도 효율적이다.

정렬의 종류 (병합, 힙, 퀵, 트리)

시간 복잡도 $n*log(n)$

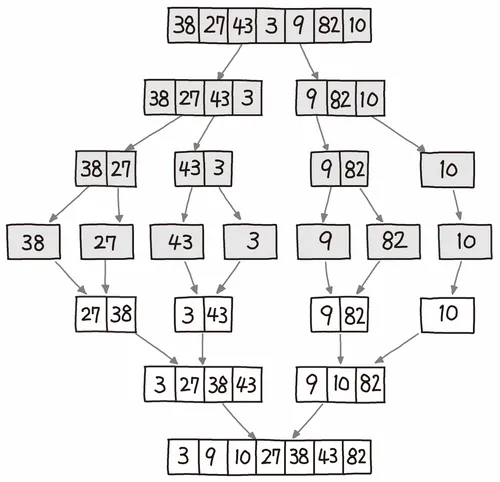
• 병합 정렬 (Merge sort)

  원소의 갯수가 0 또는 1이 될 때까지 리스트를 두 부분으로 쪼개고 쪼갠 순서의 역 순으로 크기를 비교해 병합한다.
  이때, 병합된 부분은 이미 정렬된다.
  
  성능은 퀵 정렬에 뒤떨어지고 데이터 크기를 저장할 메모리가 더 필요하다.
  
  장점은 데이터의 상태에 별 영향을 받지 않는다.
  -> 안정 정렬 같은 값의 앞 뒤 순서가 바뀌는 일이 일어나지 않음.
  A[33]=100, A[50]=100인 정수형 배열을 정렬할 때, 힙 정렬, 퀵 정렬은 50번째 100이 33번째 100보다 앞에 나열되는 경우가 생길 수 있다.
  하지만, 병합정렬은 쪼개고 값이 같으면 비교하지 않기 때문에 정렬 순서가 유지된다.
  

병합 정렬 코드

  void merge(int list[], int left, int mid, int right){
	int i,j,k,l;
	i = left;
	j = mid+1;
	k = left;
	
	while(i<=mid && j<=right){
		if (list[i]<=list[j]){
			sorted[k++] = list[i++];
		}
		else{
			sorted[k++] = list[j++];
				
		}
	}
	
	if(i>mid){
		for (l=j; l<=right; l++){
			sorted[k++] = list[l];
		}
	}
	else{
		for (l=i; l<=mid; l++){
			sorted[k++] = list[l];
		}
	}
	for (l=left; l<=right; l++){
		list[l] = sorted[l];
	}

}
void merge_sort(int list[], int left, int right){
	int mid;
	mid = (left+right)/2;
	
	if (left<right){
		merge_sort(list,left,mid);
		merge_sort(list,mid+1,right);
		merge(list,left,mid,right);
	}
}

힙 (heap)

• • 힙이란?
    
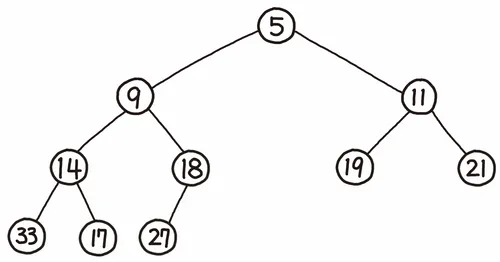
    힙(heap)은 '무엇인가를 차곡차곡 쌓아올린 더미' 라는 뜻
    힙은 항상 완전 이진트리 (위부터 아래, 왼쪽에서 오른쪽 순서로 꽉 차 있는 트리) 형태를 띠어야 하고, 부모의 값은 자식들의 값보다 항상 작거나 커야한다.
    -> 삽입/삭제의 속도 때문에 완전 이진트리 형태를 띄어야한다.
    
    
• • 데이터를 삽입하는 방법?
    
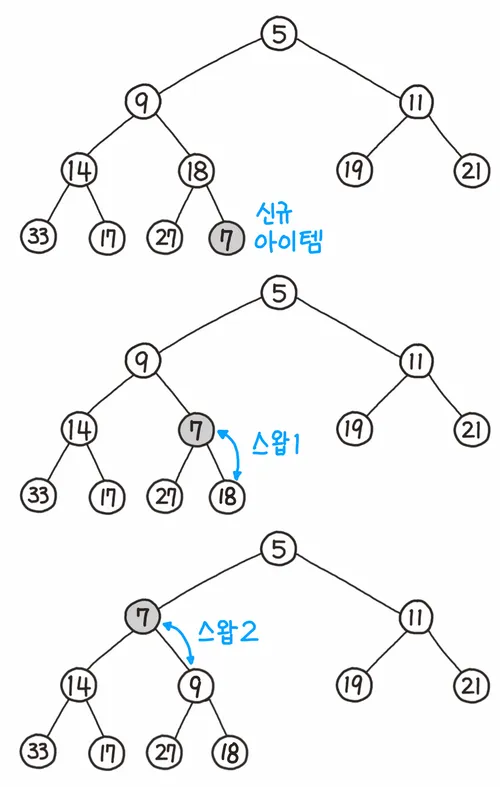
    1.가장 끝 자리에 노드를 삽입한다.
    2.노드와 부모 노드를 서로 비교
    3.규칙에 맞으면 그대로 두고, 그렇지 않으면 부모와 자리 교환
    4.규칙에 맞을 때까지 3번 과정 반복
    
    
• • 데이터 삭제
    최대 혹은 최솟값을 저장하고 있는 루트 노드만 제거할 수 있다.
    1.루트노드 제거
    2.루트 자리에 가장 마지막 노드 삽입
    3.노드와 자식 노드를 비교
    4.만족하면 그대로 두고 그렇지 않으면 자식과 교환
    
    
• • 이진 힙의 표현
    
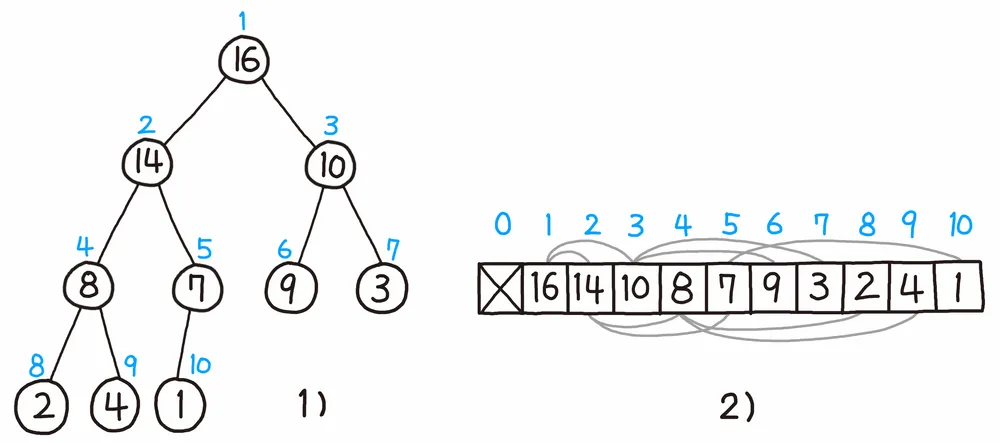
    주로 배열로 표현한다.
    -> 알고리즘을 구성할 때, 배열로 입력받아 이진힙으로 연결지어 문제 풀이
    계산 용이성을 위해 인덱스는 1부터 사용한다.

• 힙 정렬 (Heap sort)

  (1) 원소들을 전부 힙에 삽입
  (2) 힙의 루트값은 최대 혹은 최솟값이므로 루트 노드를 출력하고 힙에서 제거
  (3) 힙이 빌 때까지 2번 과정 반복
  
  선택 정렬과 유사한 알고리즘
  추가적인 메모리 공간을 필요로하지 않고,
  항상 $O(n*log n)$ 성능을 발휘

힙 정렬 코드

void max_heap(){
	for (int i=1; i<8; i++){
		int child = i;
		while ( child != 0){ //자식이랑 부모를 비교하고 자식을 부모값으로 바꾸고 연산을 계속하기 때문
			int root = (child-1)/2;
			if (arr[root]<arr[child]){
				int temp = arr[root];
				arr[root] = arr[child];
				arr[child] = temp;
			}
			child = root;
		}
	}
}

void heap_sort(){
	for (int i= 8-1; i >= 0; i--){
		int temp = arr[0]; // 마지막 노드와 최상단 루트 노드 교환
		arr[0] = arr[i];
		arr[i] = temp;
		

		int root = 0;
		int child = 1;
		
		// arr[i] 에 root 값을 채워가야함
		while(child <i){
			//root 의 자식
			child = 2*root +1;
			//더 큰 자식 찾기
			if (child <i-1 && arr[child] < arr[child+1]){
				child++;
			}
			//루트보다 자식이 크면 루트와 자식 교체
			if (child <i && arr[root] < arr[child]){
				temp = arr[root];
				arr[root] = arr[child];
				arr[child] = temp;
			}
			root = child;
		}
	}
	
}

• 퀵 정렬

  평균적인 상황에서 최고의 성능 발휘
  
  피벗(Pivot) 을 설정해서 피벗보다 작은 값은 앞으로 빼내고 그 뒤에 피벗을 옮겨 피벗보다 작은 것/ 피벗보다 큰 것 으로 나누고
  나눠진 두 그룹에 다시 피벗 설정, 각각에 피벗 설정해 위 과정 거치기 (각각의 크기가 0이나 1이 될 때까지 정렬을 반복)
  
  이렇게 피벗을 설정하고 두 그룹으로 나누는 과정을 Partition Step 이라고 하고, Partition Step 을 어떻게 하느냐에 따라 성능이 좌우되기도 한다.
  
  이때 보통 피벗은 중위법을 이용해 (첫 원소, 중간 원소, 끝 원소의 중간값) 결정하는게 가장 효율적이라고 한다.
  

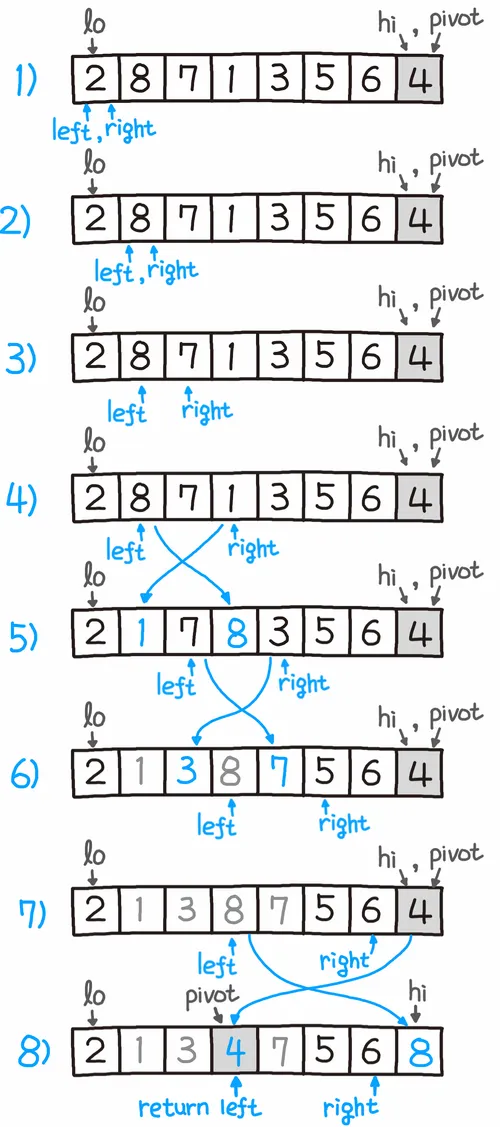
  (1) 피벗을 마지막 원소로 지정
  (2) left, right 포인터를 지정하고 left가 피벗보다 크고, right가 피벗보다 작을 때 left <-> right 스왑
  (3) (2) 과정을 right 가 피벗 직전까지 도달할때까지 반복
  (4) 피벗과 left 값 스왑
  (5) left < right 를 만족할때까지 재귀적으로 반복하면 정렬 완성
  
  이때 피벗을 최솟값 혹은 최댓값으로 계속해서 설정되면 (이미 정렬된 배열) 시간 복잡도가 $O(n^2)$ 으로 최악의 상황이 발생할 수도 있다.
  -> 재귀 깊이가 어느 한계 이상으로 깊어지면 힙 정렬 알고리즘을 사용해 $O(nlogn)$을 보장하는 방법을 사용하기도 함.

퀵 정렬 코드

void quick_sort(int start, int end){
	if (start>=end)	return ;
	int key = start, i = start+1, j=end;
	while(i<=j){
		while(i<=end && arr[i]<=arr[key])	i++;
		while(j>start && arr[j]>=arr[key])	j--;
		if (i>j)	SWAP(&arr[key],&arr[j]);
		else	SWAP(&arr[i],&arr[j]);
	}
	quick_sort(start,i-1);
	quick_sort(i,end);
}

• 트리 정렬

  이진 탐색 트리를 만들어 정렬하는 방식
  힙 정렬과 비슷하지만, 노드를 구성하는 방법이 다르다.
  왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드 로 구성되는게 특징
  
  이진 탐색 트리에서 데이터를 탐색하는 과정

  (1) 루트 노드부터 방문해 찾고자 하는 값이 루트 노드보다 큰지 작은지 확인 / 작다면 왼쪽 자식 노드로, 크다면 오른쪽 자식 노드로
  -> 1번 탐색 과정을 진행했을 때, 한쪽 트리는 필요가 없어짐으로 탐색할 필요가 없어짐.
  트리가 정확히 대칭적으로 구성되어있다면, 한번 탐색할때마다 탐색 범위가 1/2 씩 줄어든다.

  (2) 위 방법과 동일하게 오른쪽 자식 노드를 루트 노드로 설정하고 값 비교

  트리의 순회 방법
  : 트리의 노드들을 특정한 방법으로 한번씩 방문하는 방법
  
  

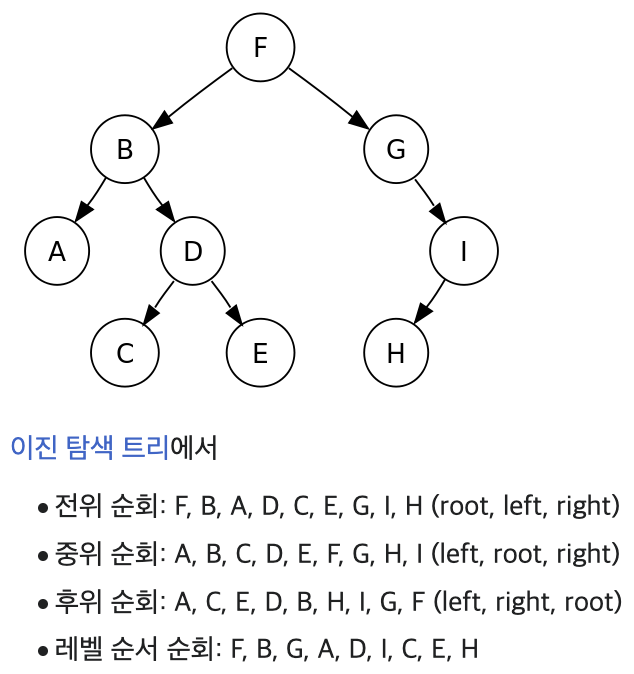
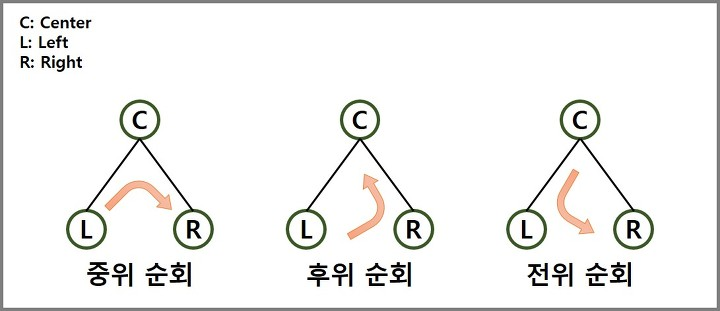
  (1) 전위 순회(pre-order traverse) : 루트 먼저 방문, 왼쪽, 오른쪽 순
  (2) 중위 순회(in-order traverse) : 왼쪽 자식, 루트, 오른쪽 순
  (3) 후위 순회(post-order traverse) : 오른쪽 자식, 왼쪽, 루트 순

  트리 정렬은 중위 순회 방식으로 이진 트리를 순회한다.

• 트리 정렬 코드

참조 - 나무위키 정렬 알고리즘