[논문 리딩] ResNet

요약

1. degradation 문제에 대한 해결책을 제시하였다.
2. 이전 모델(eg. vgg) 보다 성능이 좋고 파리미터 수도 적음, 시간(FLops)도 빠름
3. 아직까지도 backbone(feature 뽑기) 네트워크로 많이 쓰이고 있다. (Sota)
   • vision transformer(ViT)

degradation 문제

• 네트워크의 깊이는 모델의 정확도를 높이는데 매우 중요
  • 그치만 단순히 깊이만 쌓는다고 해서 능사인가? No
• 네트워크가 깊으면 발생하는 문제:
  - vanishing/exploding gradients -> normalized initialization or intermediate normalization으로 어느 정도 해결
  - degradation problem: 깊이가 깊을수록 overfitting 이외의 학습 장애가 생김(깊을수록 training과 testing error가 둘 다 커진다), accuracy saturates
  
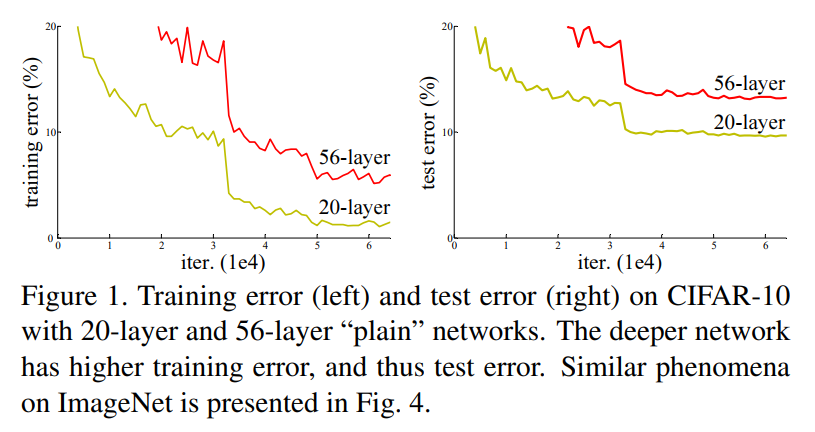
• degradation -> deep residual network (얕은 모델의 오차와 거기에 층을 추가한 깊은 모델의 오차가 크지 않도록)
  - residual mapping: 네트워크가 타깃 값이 아닌, 타깃 값에서 입력값을 뺀 잔해를 학습하도록 한다.
  - $\bold{x}$ = input, $\mathcal{H}(\bold{x})$ = desired mapping
  - $\mathcal{F}(\bold{x}) := \mathcal{H}(\bold{x}) - \bold{x}$ ( ->residual mapping) 이 값을 학습한 후 x를 더해서 기존 타깃 값 생성
  - 이렇게 하는 것이 더 성능이 좋을 것이다. -> 만약 identity mapping이 최적의 값을 도출한다면, residual을 0으로 만드는 것이 비선형 구조에서 identity를 만드는 것보다 쉬울 것.
  
  

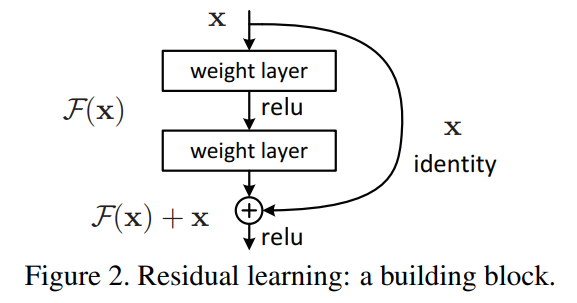
ResNet 구조

1. Residual Learning

   • 앞서 설명한 residual mapping을 통해 residue를 학습
   • training error를 줄일 수 있을 것이다. -> identity mapping으로 된 레이어가 추가된다면, 더 큰 모델의 오차는 추가되기 전 모델의 오차와 다를 것이 없다. 학습하다 필요 없는 레이어(identity가 optimal한 경우) weight를 0으로 하면 된다(0 + x = x).
   • 단순하게 생각하면, 본 값을 학습하는 것보다 차이를 학습하는 것이 더 빠를 것이다.

2. Identity Mapping by Shortcuts

   • identity mapping: element-wise addition

     $\bold{y}=\mathcal{F}(\bold{x},\{W_i\})+\bold{x}$

   • projection shortcuts:

     $\bold{y}=\mathcal{F}(\bold{x},\{W_i\})+W_s\bold{x}$

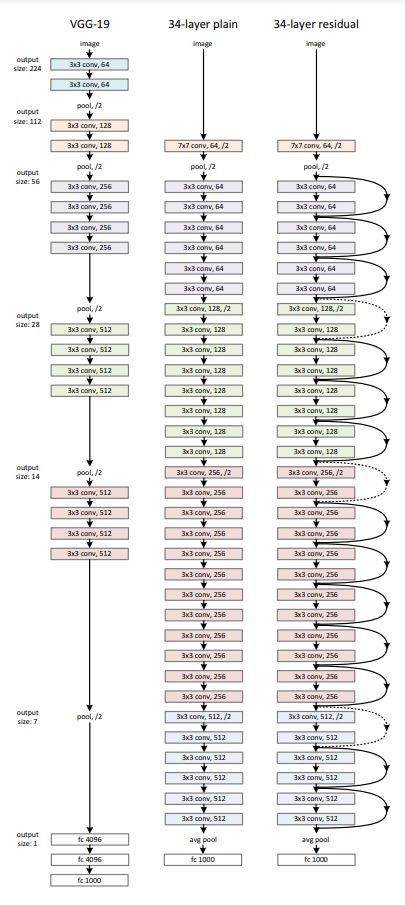
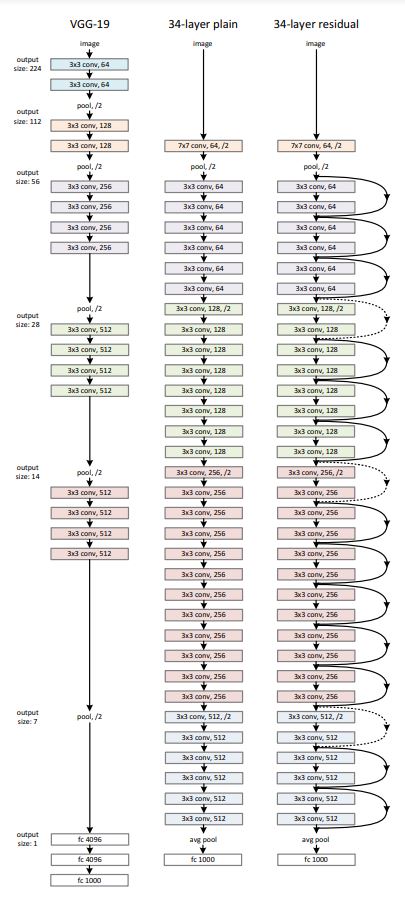
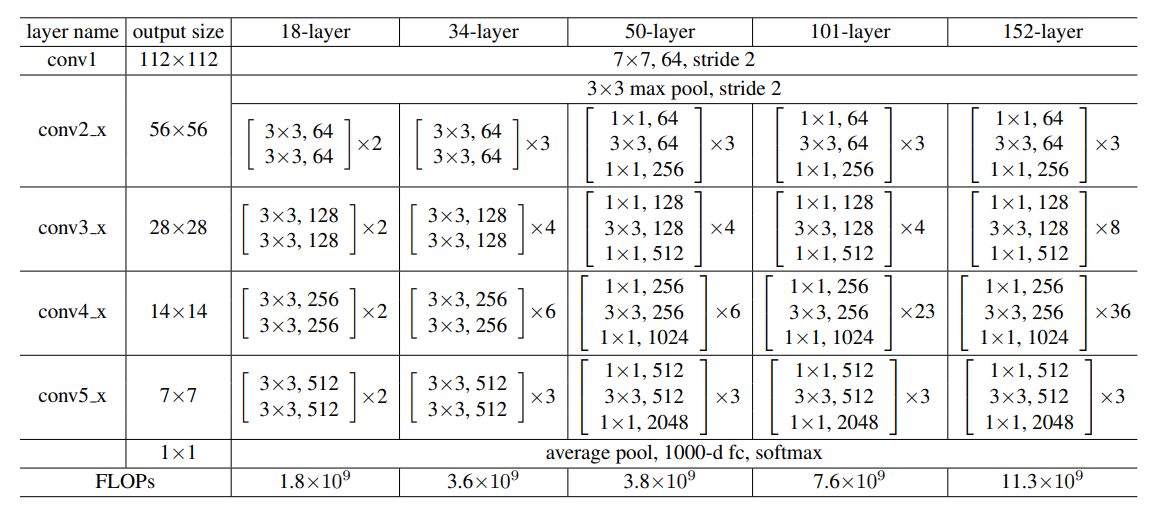
3. Network Architectures

   • plain network: VGG와 비슷한 구조. feature map이 /2로 downsample 시 필터 수 2배로, 아닌 경우 동일하게 유지. 마지막에 GAP(global average pooling) + 1000-way fc layer with softmax
   • residual network: plain network + shortcut connections.
     • 채널 수가 같은 경우 단순히 더한다(identity shortcuts).
     • 더 큰 경우(2배):
       (1) identity mapping with zero padding
       (2) projection shortcut with 1x1 convolution to match dimensions -> new parameters to learn
       => 둘 다 stride 2로 downsample

4. Implementation
   - conv + BN(Batch Normalization) + activation(ReLU)
   

Codes

-작성중-