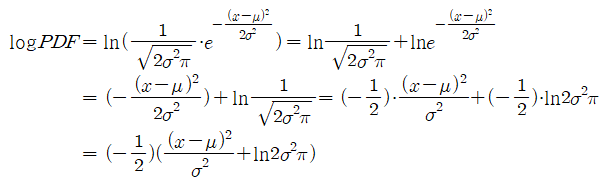Naive Bayesian classifier
Naive Bayesian classifier는 Bayes theorem을 베이스로 하는 확률기반 분류모델이다. Bayes theorem은 조건부 확률을 계산하는 방법 중의 하나로, 본 모델의 classifier에서 주요부분을 담당하고 있는 사후확률(posterior) 계산을 위한 정리를 이야기한다. Bayes theorem을 사후확률 계산에 적용하기 위해서는 특정 개체를 규정짓는 여러 feature들이 서로 독립적이라 가정하여야 하는데, 이러한 부분을 두고 Naive(순진한)라는 표현으로 본 모델을 나타내게 된 것이다. 예를 들어, 특정 과일을 사과로 분류 가능하게 하는 feature들(둥글다, 빨갛다, 지름 약 10cm)은 Naive Bayes classification에서 feature들 사이에서 발생할 수 있는 연관성이 없음을 가정하고 각각의 feature들이 특정 과일이 사과일 확률에 독립적으로 기여하는 것으로 간주한다.
Naive Bayes classification은 일부 확률 모델에서 지도 학습 환경의 훈련을 매우 효율적으로 만들어줄 수 있다. parameter의 추정은 MLE(Maximum Likelihood Estimation)를 사용한다. 또한 다른 classifier에 비해 classification에 필요한 parameter를 추정하기 위한 학습 데이터의 양이 매우 적으며, 간단한 design과 단순한 가정에도 불구하고 많은 복잡한 실제 상황에 잘 작동한다는 것이 Naive Bayes classification의 장점으로 알려져 있다.
Bayes theorem
Naive Bayes classification에서 Bayes theorem은 사후확률(posterior probability)를 구하기 위해 활용된다. 일반적으로 조건부확률을 구하기 위해서는 아래와 같은 수식을 사용해야 한다.
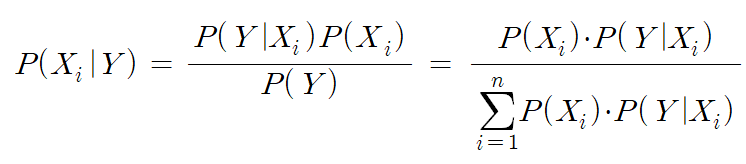
우리가 구현하게 될 Naive Bayesian classifier에서 위의 식을 해석한다면, 각각의 값들이 다음과 같은 의미를 갖는다.
prior probability는 class에 대한 사전 확률로, 본 포스팅에서 prior probability는 단순하게 test data set 내에서 각 class가 가지는 비중을 의미한다고 봐도 무방하다. 우리는 앞으로 고정된 class에 대한 확률을 가지고 위의 식 전체 값을 의미하는 posterior probability를 비교하게 될 것이기 때문에, 공통적으로 분모에 곱해져있는 evidence값은 본 포스팅에서는 상수라고 보고 처리하여도 무방하다.
feature의 개수가 한 가지보다 많을 때를 생각해보자. i번째 class인 X_i의 data가 k개의 feature를 가지고 있다고 하면, Bayes theorem에서는 확률변수 X_i가 가지는 feature들이 모두 독립적이라 가정하기 때문에, 다음과 같은 방법으로 chain rule을 이용하여 다른 형태의 posterior를 구할 수 있다.
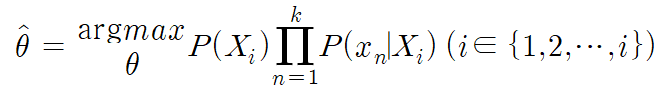
새로 입력되는 data인 x에 대하여 위의 식들의 의미를 생각해보자. P(x|Xi)는 likelihood로, Xi class 내에서 x라는 데이터가 발생할 확률을 의미하고, P(Xi|x)는 posterior로, x라는 데이터가 Xi class 내에 속해있을 확률을 의미한다. data가 k개의 feature를 가지고 있다고 하면, x라는 데이터가 갖는 feature값들을 x1,x2,...,xk로 표현할 수 있다. 이러한 feature값 들이 동시에 발생하였을 때 해당 값이 Xi class에 속해있을 확률을 P(Xi|x1,x2,...,xk) 라 표현하고, 이는 posterior인 P(Xi|x)와 같은 의미를 갖는다. 또한 classifier의 역할을 수행하기 위해서는 (특정 feature값들을 동시에 갖는 새롭게 입력되는) data가 각 class에 속해있을 확률을 비교하여야 하므로, 다음과 같은 식으로 classifier를 나타낼 수 있다.
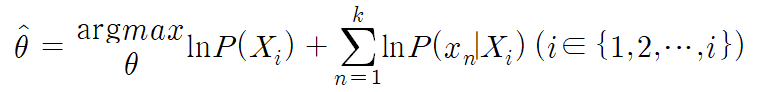
또한, classifier의 구현을 위해 posterior값은 대소비교만을 위해서만 사용될 것이다. 따라서 전 구간 증가하는 추세를 가지면서 y=x보다 좁은 y값 변화 스케일을 가진 로그를 취해 다음과 같이 posterior 값을 대신할 수도 있다.
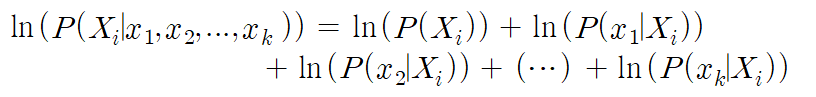
이와 같이 로그를 취하면, class의 수가 증가하여도 곱연산을 합연산으로 대신하여 처리할 수 있기 때문에 실제 성능을 향상시킬 수 있을 것으로 예상된다. 따라서 다음과 같은 식으로도 classifier를 나타낼 수 있다.
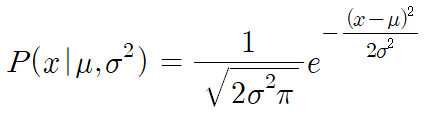
Gaussian PDF(Probability Density Function)
가장 널리 쓰이는 정규분포를 의미하며, 파라미터가 두 개만 있어도 형태가 결정되는 선형 확률분포이다. Gaussian PDF는 mu(mean), sigma(standard deviation)를 parameter로 하여 나타나는 확률분포이며, 함수식은 다음과 같다.
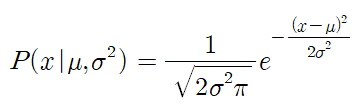
Naive Bayesian classifier 구현
본 예제에서 구현되는 Naive Baysian Classifier는 Gaussian PDF를 분포로 하며, csv확장자로 저장되어 있는 dataset은 2차원 배열의 형태를 띄고 있다. 이는 총 150개의 data를 포함하고 있다. 각 data들은 4개의 feature값과 3개의 class 중 한 개의 class 값을 label로 가지고 있다.
-
pre-processing
feature normalization에 앞서 프로그램은 주어진 데이터파일(csv)을 불러오고, 원활한 학습과 테스트를 위해 shuffling하는 과정을 거친다. 이후 datafile을 python numpy 배열로 변환한 뒤, 라벨과 데이터로 분류하고, 라벨의 개수를 추출해낸다. 일련의 preprocessing이라고 할 수 있다. 웹 크롤링이나 API 호출 등을 통해 얻어온 데이터를 구현해놓은 알고리즘의 input으로 사용할 수 있는 양식으로 변환하는 과정이다. 일반적으로는 수집된 데이터를 정제, 통합, 축소하는 등 더욱 많은 과정을 거치지만, 본 포스팅에서는 정제되어 제공된 상태의 dataset을 활용하기 때문에 간략하게 양식만 필요에 따라 변환해주는 과정을 거쳤다. -
feature normalization
feature normalization 과정에서 main함수는 feature_normalization함수를 호출하여 앞서 가공한 data를 파라미터로 건네주고, return으로 돌려받은 값을 normalled_data에 저장한다. 그 뒤, normalization 과정의 전과 후의 평균을 출력하여 값이 적절하게 변환되었는지 확인한다. -
split test data and train data
-
train classifier
classifier를 학습시키는 과정은 train data와 test data로 나뉘어진 data 중에서 train data를 이용하여 각 class별로 gaussian PDF의 normal parameter(mu:mean, sigma: standard deviation)을 구하고, 각 class의 prior probability를 구하는 과정이다. -
test classifier
학습시킨 classifier를 test하는 과정이며, 실제 classification을 수행하는 과정이다. 앞서 split을 통해 확보해둔 test dataset으로 진행하며, test dataset의 data가 어떤 class에 속하는 지 prediction하는 것이 목표이다.
source code
# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
def feature_normalization(data):
feature_num = data.shape[1]
data_point = data.shape[0]
normal_feature = np.zeros([data_point, feature_num])
mu = np.zeros([feature_num])
std = np.zeros([feature_num])
mu = np.mean(data,axis=0) # get mean of data
std = np.std(data,axis=0) # get standard deviation of data
for i in range(data_point): # calculate normalization data
for j in range(feature_num):
normal_feature[i][j] = (data[i][j] - mu[j]) / std[j]
# Normalization data x_ = (x - mu) / sigma
return normal_feature
def split_data(data, label, split_factor):
return data[:split_factor], data[split_factor:], label[:split_factor], label[split_factor:]
def get_normal_parameter(data, label, label_num):
feature_num = data.shape[1]
mu = np.zeros([label_num,feature_num])
sigma = np.zeros([label_num,feature_num])
for i in range(label_num): # i is label number
class_ = [] # let's collect i class data.
for j in range(len(data)): # j is data number
if label[j] == i: # if 'jth data' is in 'i class',
class_.append(data[j]) # append 'jth data' to class array
class_ = np.array(class_)
mu[i] = np.mean(class_, axis=0) # get mu(mean) of i class
sigma[i] = np.std(class_, axis=0) # get sigma(standard deviation) of i class
return mu, sigma
def get_prior_probability(label, label_num):
data_point = label.shape[0]
prior = np.zeros([label_num])
for i in range(label_num): # let's get the prior of each class.
for j in range(data_point):
if(label[j] == i):
prior[i] += 1 # count datas included i class
prior[i] /= data_point # divide number of class by number of data
return prior
def Gaussian_PDF(x, mu, sigma):
# calculate a probability (PDF) using given parameters
pdf = 0
pdf = 1
pdf /= sigma * np.sqrt(2 * np.pi)
pdf *= np.exp(-((x-mu)**2)/(2*(sigma**2)))
# calculate gaussian PDF
# pdf = (1 / np.sqrt(2 * np.pi * (sigma ** 2))) * np.exp(-((x - mu) ** 2) / (2 * (sigma ** 2)))
return pdf
def Gaussian_Log_PDF(x, mu, sigma):
# calculate a probability (PDF) using given parameters
log_pdf = 0
log_pdf = ((x - mu)**2) / sigma**2
log_pdf += np.log(2 * (sigma**2) * np.pi)
log_pdf *= -0.5
# calculate natural log of gaussian PDF
# log_pdf = -(0.5)*(((x - mu) ** 2 / sigma ** 2) + np.log(2 * np.pi * (sigma ** 2)))
return log_pdf
def Gaussian_NB(mu, sigma, prior, data): # 40 points
data_point = data.shape[0]
label_num = mu.shape[0]
likelihood = np.zeros([data_point, label_num])
posterior = np.zeros([data_point, label_num])
## evidence can be ommitted because it is a constant
for i in range(data_point):
for j in range(label_num):
likelihood[i][j] = 1
for feature_probability in Gaussian_PDF(data[i], mu[j], sigma[j]):
likelihood[i][j] *= feature_probability # use chain rule.
posterior[i][j] = prior[j] * likelihood[i][j]
# P(Y)*P(X1 and X2 and X3|Y) = P(Y) * P(X1|Y) * P(X2|Y) * P(X3|Y)
# we can use this code↓ instead of line(105~108).
# likelihood[i][j] = 0
# for feature_probability in Gaussian_Log_PDF(data[i], mu[j], sigma[j]):
# likelihood[i][j] += feature_probability
# posterior[i][j] = np.log(prior[j]) + likelihood[i][j]
# ln(P(Y)*P(X1 and X2 and X3|Y)) = ln(P(Y)) + ln(P(X1|Y)) + ln(P(X2|Y)) + ln(P(X3|Y))
return posterior
def classifier(posterior):
data_point = posterior.shape[0]
prediction = np.zeros([data_point])
prediction = np.argmax(posterior, axis=1)
return prediction
def accuracy(pred, gnd):
data_point = len(gnd)
hit_num = np.sum(pred == gnd)
return (hit_num / data_point) * 100, hit_num
def main():
# data loading using pandas
df = pd.read_csv('iris.csv')
# categorical label to numerical label
df['variety'] = df['variety'].astype('category').cat.codes
# shuffling
df = df.sample(frac=1).reset_index(drop=True)
# separation of data and labels
data = df.iloc[:, :-1].to_numpy()
label = df.iloc[:, [-1]].to_numpy().squeeze()
label_num = max(label) + 1
# feature normalization
normalled_data = feature_normalization(data)
print("Mean:", np.mean(data, 0))
print("normalled_Mean:", np.mean(normalled_data, 0))
data = data # or normalled_data
# spilt data for testing
# 100 => training data : 100 / test data : 50
split_factor = 100
training_data, test_data, training_label, test_label = split_data(data, label, split_factor)
# get train parameter of nomal distribution and prior probability
mu, sigma = get_normal_parameter(training_data, training_label, label_num)
prior = get_prior_probability(training_label, label_num)
# get postereior probability of each test data based on likelihood and prior
posterior = Gaussian_NB(mu, sigma, prior, test_data)
# classification using posterior
prediction = classifier(posterior)
# get accuracy
acc, hit_num = accuracy(prediction, test_label)
# print result
print(f'accuracy is {acc}% !')
print(f'the number of correct prediction is {hit_num} of {len(test_label)} !')
if __name__ == "__main__":
main()Gaussian_PDF함수식
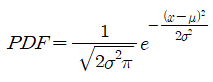
Gaussian_Log_PDF 함수식
