
5강에서는 Fully Connected Neural Networks에서 Convolutional Neural Networks로 이동한다.
Perceptron, Neocognition, LeNet, AlexNet을 포함하여 Convolutional Networks 개발의 역사에 대해 논의한다.
현대 Convolutional Networks의 기반을 형성하는 Convolution, Pooling, Fully-connected layers를 소개한다.
CNN의 역사
최초로 perceptron 구현
-
1957년 Frank Rosenblatt가 Mark I Perceptron machine을 개발
-
가중치 W를 업데이트하는 update rule
Multilayer Perceptron Network
- 1960년 Widrow와 Hoff가 Multilyaer perceptron network인 Adaline/Madaline 개발
Backpropagation, 신경망
- 1986년 Rumelhart 최초로 backpropagation 제안, 신경망 학습 시작
Deep Learning
-
2006년 Geoff Hinton과 Ruslan Salakhutdinow
-
weight를 잘 줄 수 있도록 RBM으로 초기화
-
그 후 전체 신경망을 fine-tunning with backpropagation
AlexNet
-
2012년 Hintin lab
-
deep learning이 확 뜨기 시작
-
ImageNet classification에서 CNN을 사용해 결과 좋았음 ➡️ 이때부터 CNN 널리 사용
CNN
1950년 Hubel과 Wiesel
-
뇌의 특정 뉴런은 특정 방향에 반응한다는 것을 발견
➡️ topographical mapping -
뉴런이 계층구조를 가진다는 것을 발견
- Simple cells -> Complex cells -> Hypercomplex cells (큰 -> 섬세 영역)
1980년 Fukushima
- Neocognitron
- simple cells과 complex cells를 샌드위치 구조로 반복적으로 쌓음
(큰 -> 섬세 영역) - backpropagation 불가능
- simple cells과 complex cells를 샌드위치 구조로 반복적으로 쌓음
1998년 Yann LeCun
- 글자 인식에 gradient-based learning 적용
- backprpagation 가능
2012년 Alex Krizhevsky
- AlexNet 제안
- CNN의 현대화된 모습
- 1998년에 나온 것과 구조는 다르지 않으나 더 크고 깊어졌다.
- 마찬가지로 큰 -> 섬세 영역으로 특징 추출
-
대규모 데이터 활용, 처음으로 GPU 2대 사용
-
가중치 초기화를 잘했고 batch normalization 진행
-
ImageNet에서 엄청난 정확도
CNN 활용
-
이미지 분류/검색
-
Detection (실시간 detection을 하는 YOLO)
-
Segmentation (각 픽셀에 라벨링)
-
자율주행 (Lidar를 통해)
-
face recognition
-
pose recognition (게임에 활용 가능)
-
비디오 인식 (시간적 정보 활용)
-
의학 영상 해석/진단
-
은하/표지판 인식
-
고래 분류 / 항공지도를 통한 길과 건물 인식
-
image captioning
- segmentaion을 하는 CNN & text generation을 하는 RNN 동시 사용 가능
-
글을 보고 이미지를 만들어 내는 Open AI의 Dall-E도 CNN 사용
-
style transfer
- GAN 사용
- 특정 화풍으로 그림
CNN의 원리
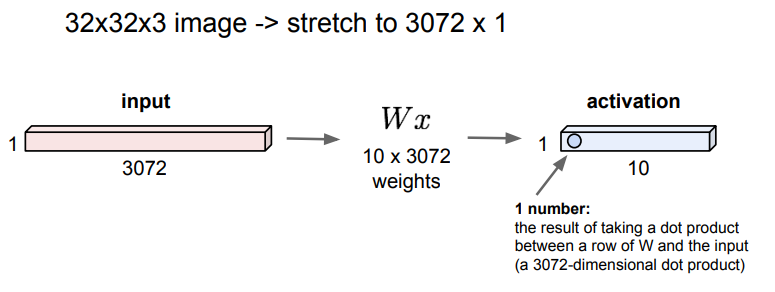
이전에 다뤘던 Fully Connected Layer는 32x32x3 이미지를 펴서 3072x1인 벡터 x로 만들고, 가중치 W와 내적 연산을 해 1x10의 activation layer에 출력하는 방식
Convolutional Layer
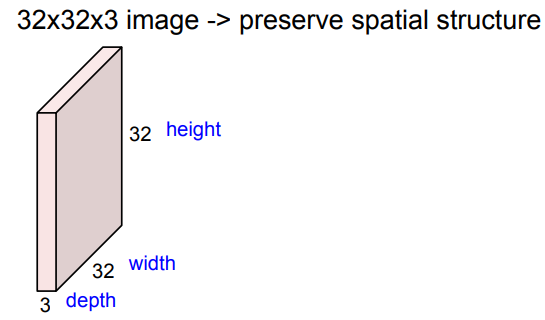
Fully connected layer와 달리 Convolutional Layer는 기존의 structure을 유지한다.
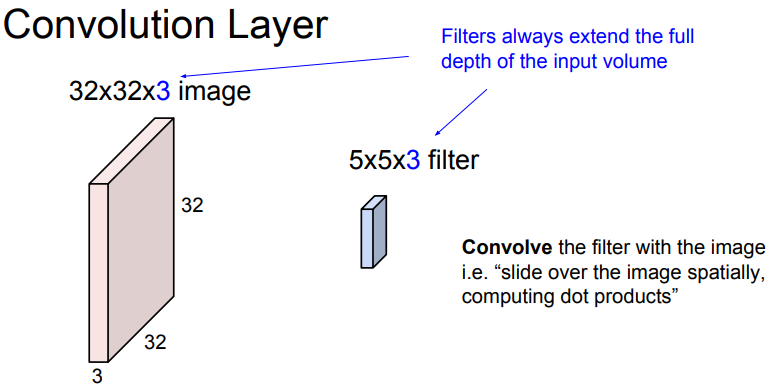
Convolution layer는 filter와의 공간적 내적을 통해 한 개의 숫자를 출력한다.
➡️ 입력 이미지에 filter를 움직이면서 하나의 값을 추출
Convolve : 입력 이미지에 filter를 슬라이딩하여 내적을 구하는 것을 convolve한다고 말한다.
📌 filter의 가로/세로 크기는 선택할 수 있지만, filter의 depth는 input의 depth와 항상 같아야 한다. (모든 depth에 대해 내적이 진행되어야 하기 때문)
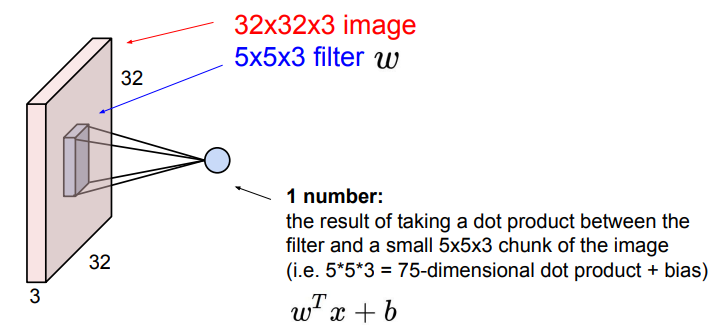
Convolution layer에 filter를 convolve하면 한 개의 숫자가 나온다. (convolve 한 번에 숫자 하나가 나온다.)
➡️ 식은 위 그림 참고
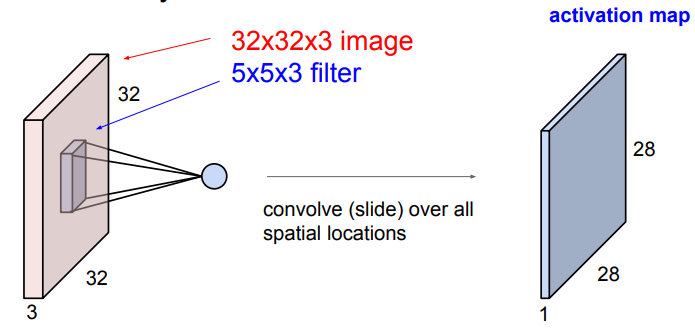
32x32x3 이미지에 5x5x3 filter를 좌측 상단부터 우측 하단까지 convolve한 값들을 모으면 28x28x1 이미지를 얻게 된다.
➡️ activation map
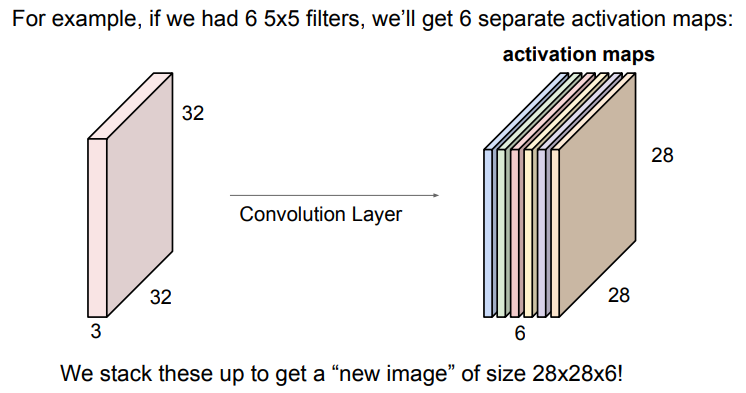
각 filter는 이미지로부터 한 개의 특징을 추출한다.
보통 CNN에서 convolution layer는 여러 개의 filter를 사용하기 때문에, filter 개수만큼의 특징을 추출할 수 있다.
위의 예제를 보면 5x5 크기의 filter가 6개가 있을 때 우리는 6개의 activation maps를 모아 28x28x6의 "새 이미지"를 얻을 수 있다.
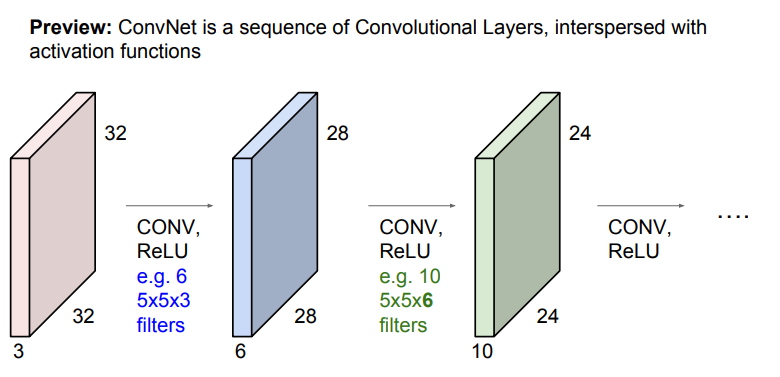
CNN에서는 입력 이미지가 Convolution layer와 활성함수 ReLU를 통과하여 activation map을 생성하고, 이 activation map에 다시 conv. layer와 ReLU를 통과하여 다시 activation map을 생성하는 과정을 반복한다.
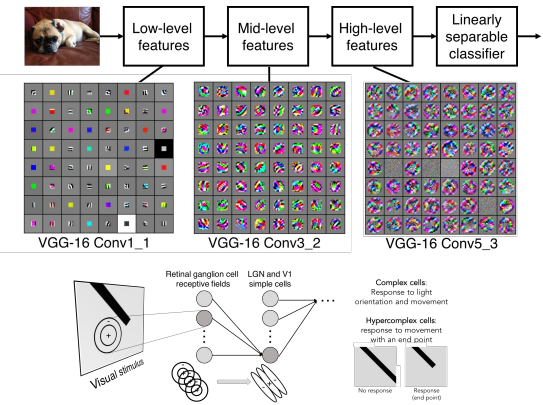
filter가 여러 개일 때, filter는 이미지의 특징을 단순->복잡하게 계층적으로 학습하게 된다.
-
첫 번째 필터 VGG-16 Conv1_1
- Low-level features인 edges, color를 학습
-
두 번째 필터 VGG-16 Conv3_2
- Mid-level features인 corner, blobs를 학습
-
세 번째 필터 VGG-16 Conv5_3
- High-level features를 학습
➡️ Convolution layer가 여러 개 쌓여 깊어질수록 이미지의 특징을 더 많이 추출

1개 filter ➡️ 1개 activation map 생성, 1개 입력 이미지 특징 추출

위의 슬라이드는 ConvNet의 각 층을 어떻게 쌓는지 보여주고 있다.
Conv. layer에 ReLU를 쌓고, Pooling layer를 쌓는 방식을 반복한다.
마지막에 Fully connected layer를 통해 이미지를 클래스별로 분류하고 스코어를 계산한다.
output size 계산
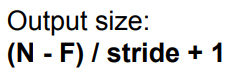
N: input size, F: filter size
stride를 통해 filter를 몇 칸씩 움직일지 정할 수 있다.
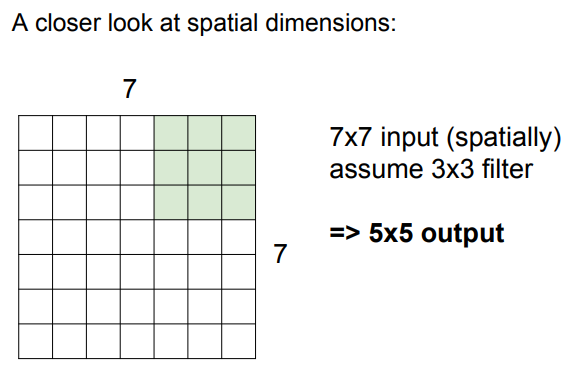
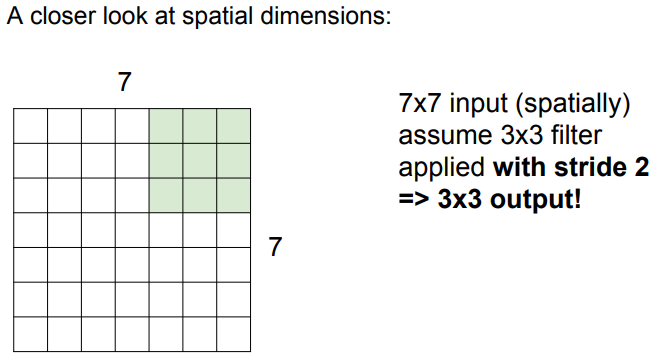

📌 슬라이딩 시 input 크기와 딱 맞아 떨어지는 stride만 사용한다.
➡️ 맞아 떨어지지 않을 경우 zero-padding을 통해 해결 가능!
zero-padding

위에서 stride가 3일 때 슬라이딩 시 input size와 맞아 떨어지지 않아 사용할 수 없었는데, 이런 경우 zero-padding을 통해 해결할 수 있다.
➡️ input image의 가장자리에 0으로 이루어진 pixel을 붙여준다.
👍장점
입력 이미지보다 작은 크기의 출력 이미지가 나오면, filter가 슬라이딩하지 못하는 입력 이미지의 모서리 부분의 정보가 누락된다.
📌
stride 1,FxF 크기의 filter를 사용할 때,(F-1)/2개의 zero padding을 하면 입력 이미지와 같은 크기의 출력 이미지(activation map)가 나온다.
➡️ 입력 이미지의 가장자리 부분의 정보까지도 출력 이미지에 잘 전달할 수 있다!
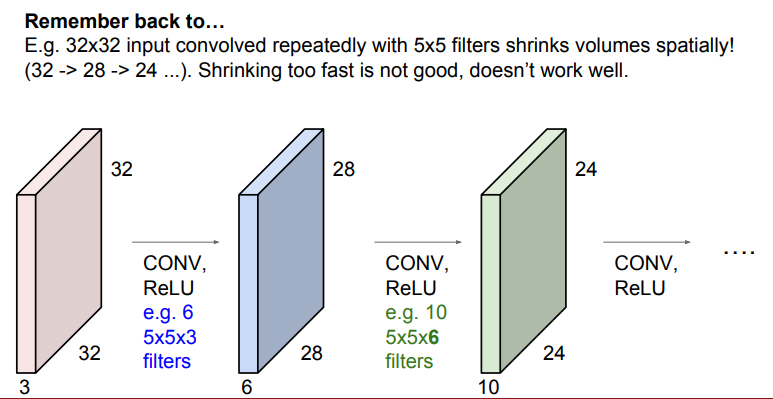
위의 슬라이드를 보면 32x32 입력 이미지에 5x5 filter를 반복하여 슬라이딩하면 출력 이미지(activation map)의 크기가 28, 24, ...로 빠르게 줄어드는 것을 볼 수 있다.
➡️ 정보가 빠르게 손실된다는 뜻
➡️ 모든 layer를 통과했을 때, 손실이 많아서 정확한 정보를 추출할 수 없다.
📌 입력 이미지와 출력 이미지의 크기가 같게 하는 이유: Convolution layer를 거치면서 이미지의 크기가 줄면, 거대한 신경망을 통과할 때 더 이상 convolve할 수 없게 된다.
➡️zero padding을 통해 출력 이미지의 크기를 보존하고pooling을 통해 이미지의 크기를 줄인다.
예제
Q. Output volume size?

📌 output volume size: NxN 입력 이미지에 P만큼 zero padding한 후, K개의 FxF의 filter를 stride만큼 슬라이딩하면
A = (N+2*P-F)/stride + 1
activation map size:AxAxK
Q. Number of parameters?
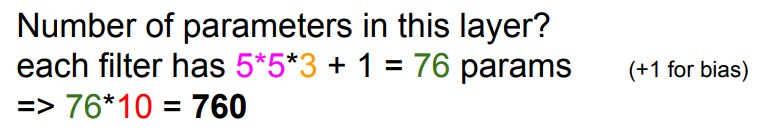
각 filter가 5x5x3이므로 5*5*3 + 1(bias) = 76개 파라미터
➡️ filter가 10개 있으므로 76*10=760
summary

ConvNet에 필요한 하이퍼파라미터
-
K: filter의 개수- 일반적으로 2^n
-
F: filter의 크기 -
S: stride -
P: zero padding의 수
이제 뉴런과 연관지어 보자.
5x5 필터가 있다면 한 뉴런의 Receptive field가 5x5라고 한다. Receptive field란 한 뉴런이 한 번에 수용할 수 있는 영역을 의미한다.
또한, 만약 총 5개의 필터를 아래와 같이 거쳤다면, 한 점에서 depth 방향으로 바라보면, 이 5개는 정확하게 같은 지역에서 추출된 서로 다른 특징이다. 즉, 공간적 의미를 그대로 가져갈 수 있다.

Pooling, ReLU
CNN에 들어가는 다른 Layer들도 살펴보자.
Pooling Layer
-
Representation들을 더 작고 관리하게 쉽게 해줌
-
DownSample
-
공간적인 invariance
-
Depth는 그대로 둠
-
차원 계산은 (width-Filter)/Stride+1
-
보통 padding 안함( 코너 값 계산 못하는 경우 없다.)
-
2x2, 3x3, stride=2 많이 씀

Max Pooling
-
필터 크기와 stride 정하면 됨
-
필터 안에 가장 큰 값 고름
-
겹치지 않게 풀링 함
ReLU Layer
-
실제 방식과 가장 유사한 비선형함수
-
활성화할지 비활성화 할지 결정
-
젤 많이 씀
stride를 설정해 줌으로써 Pooling으로 Downsampling할 수 있고, 더 좋은 성능을 가져다주기도 한다. 이는 activation map의 사이즈를 줄이는 것이고, 나중에 FC layer의 파라미터의 수가 줄어들게 된다.
Down-sampling: 딥러닝에서 인코딩할 때 data의 개수를 줄이는 처리 과정
참고)
자료: http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture5.pdf
https://velog.io/@guide333/%ED%92%80%EC%9E%8E%EC%8A%A4%EC%BF%A8-CS231n-5%EA%B0%95-2-Neural-Networks
