

Overview
-
One time setup
- activation functions
- preprocessing
- weight initialization
- regularization
- gradient checking
-
Training dynamics
- babysitting the learning process
- parameter updates
- hyperparameter optimization
-
Evaluation
- model ensembles
Part 1에서 다루는 내용
- Activation Functions
- Data Preprocessing
- Weight Initialization
- Batch Normalization
- Babysitting the Learning Process
- Hyperparameter Optimization
1. Activation Functions
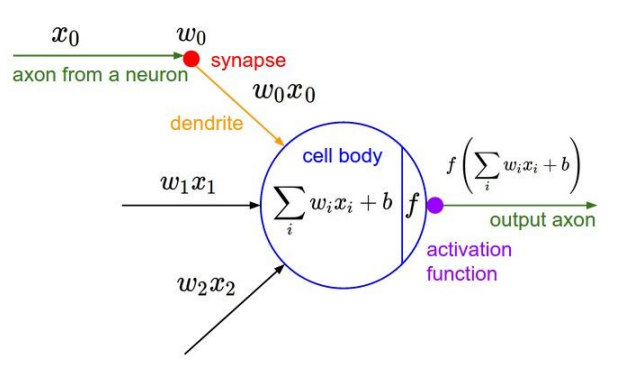
📌 활성화 함수는 비선형성을 가해주는 매우 중요한 역할!
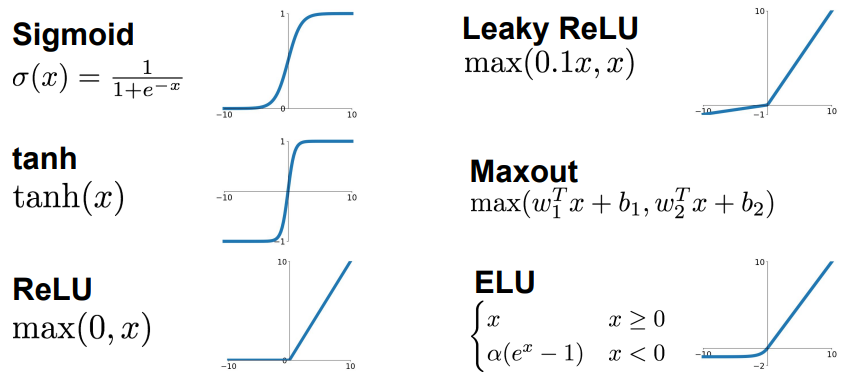
Sigmoid
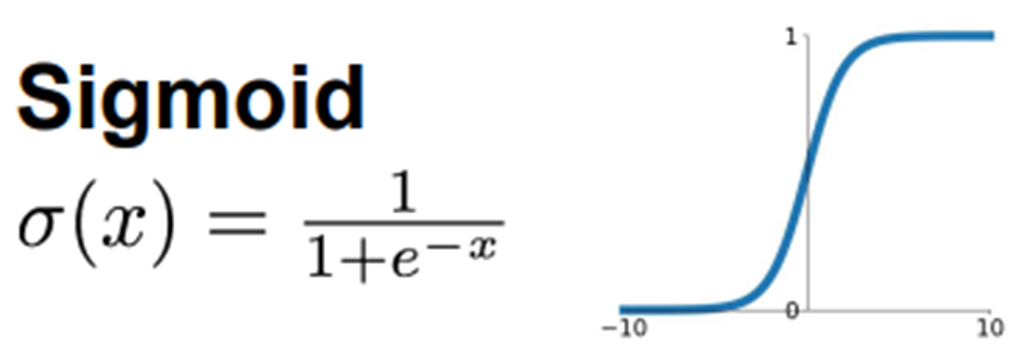
-
Output 값을 0 ~ 1로
-
대부분의 경우에서 Sigmoid 함수는 좋지 않기 때문에 잘 사용하지 않음
➡️ binary classification 경우 예외로 Sigmoid 함수를 사용 -
그래프를 보면 input값이 어느정도 크거나 작으면 기울기가 아주 작아짐
➡️Vanishing gradient문제
➡️ 역전파 어려움
Vanishing gradient
: Sigmoid로 여러 layer를 쌓았을 때, 입력층 쪽으로 갈수록 대부분의 노드에서 기울기가 0이 되어 결국 gradient가 사라짐.
- output 값이 항상 양수 ➡️
zero-center문제- Neural network는 층을 계속 쌓기 때문에 이전 노드의 output 값이 다음의 입력값이 된다. 따라서 input 값도 항상 양수만 들어온다.
입력값이 항상 양수이면 gradient는 전부 양수이거나 음수가 된다!
➡️ 아래 슬라이드처럼 가중치가 지그재그로 업데이트되기 때문에 매우 비효율적!!

👍장점: binary classification을 사용할 때
👎단점: Vanishing gradient, zero-center, exp 연산
tanh
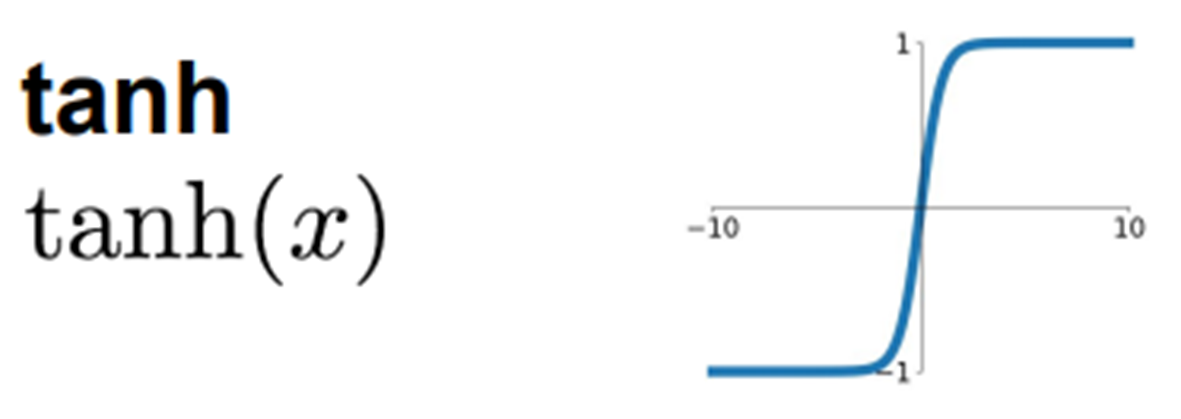
-
Sigmoid 함수와 유사
- 공통점: Vanishing gradient
- 차이점: output 값이 -1 ~ 1
-
대부분의 경우에서 Sigmoid 함수보다 성능이 좋음
👍장점: Sigmoid보다 대부분의 경우에서 학습이 더 잘 됨
👎단점: Sigmoid와 마찬가지로 Vanishing gradient
ReLU
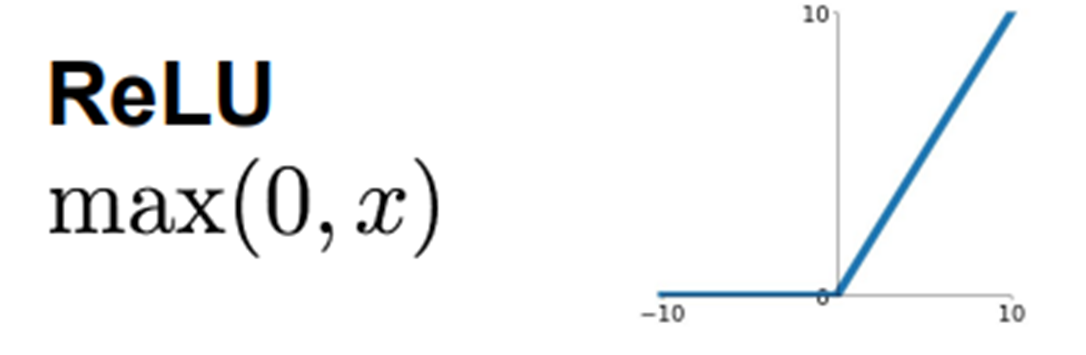
-
일반적으로 ReLU의 성능이 가장 좋아서 많이 사용
-
대부분의 input 값에 대해 기울기가 0이 아니기 때문에 학습이 빨리 됨
➡️ 학습을 느리게 하는 원인이 gradient가 0이 되는 것
➡️ hidden layer에서 대부분 노드의 z값이 0보다 크기 때문에 기울기가 0이 되는 경우가 적음 -
x가 0보다 작을 경우, 기울기가 0이기 때문에 학습 과정에서 뉴런이 죽는 경우가 생겨 값이 더 이상 업데이트 되지 않음
- 입력값의 음의 부분은 0으로 두기 때문에 여전히
vanishing gradient,zero-ceterred output이 문제!
- 입력값의 음의 부분은 0으로 두기 때문에 여전히
👍장점: 대부분의 경우에서 기울기가 0이 되는 것을 방지해주기 때문에 학습이 빠르게 잘 됨
👎단점: z가 음수일 때 기울기가 0
Leaky ReLU

-
ReLU의 단점을 해결하기 위해 등장한 함수
➡️ x가 0이하인 구간에 죽는 뉴런이 생겨 학습을 할 수 없었던 문제 -
ReLU와의 차이점: max(0,z)가 아니라 max(0.1z, z)
➡️ input 값인 z가 음수일 경우 기울기가 0이 아닌 0.1 -
많이 쓰이진 않지만 ReLU보다 학습이 더 잘 됨
👍장점: ReLU보다 학습이 더 잘 됨
👎단점: 음수에서 선형성이 생겨 복잡한 분류에선 사용 불가
Maxout
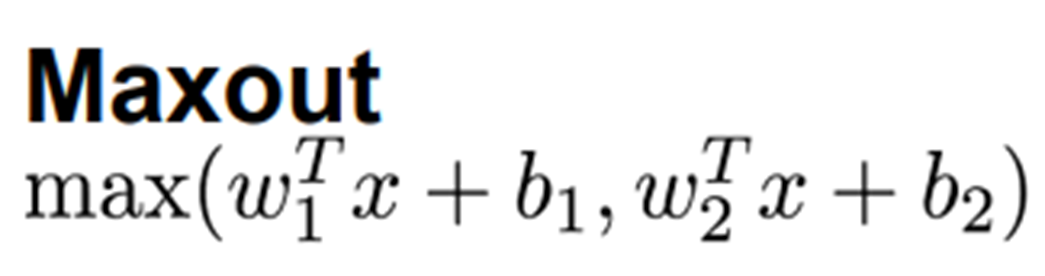
-
ReLU와 Leaky ReLU를 일반화한 함수
➡️ ReLU가 가진 장점을 모두 가짐 -
각 노드별로 학습을 시켜야 할 파라미터 weight, bias를 추가
➡️ 연산량이 두 배 이상 증가 -
성능 대비 인기 없음
👍장점: ReLU의 장점
👎단점: 연산량 증가
ELU
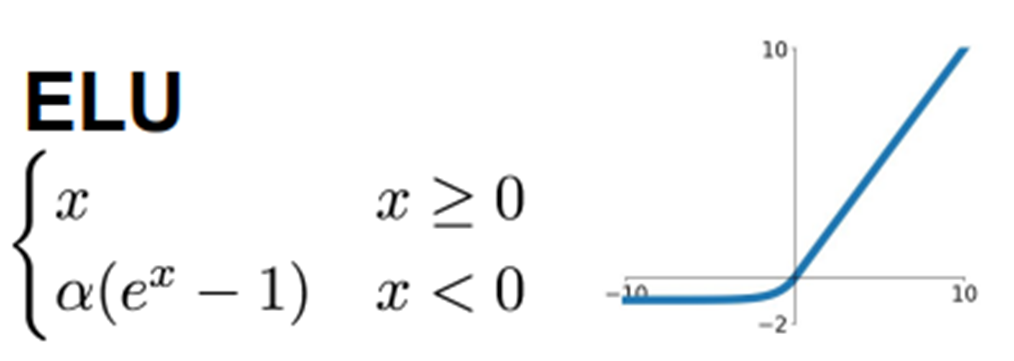
-
ReLU가 가진 장점을 가짐
-
ReLU와의 차이점: 하이퍼파라미터 α는 x가 음수일 때 수렴하는 값을 정의 (보통 1)
➡️ Leaky ReLU처럼 죽은 뉴런을 만들지 않는다는 장점
➡️ α가 1일 때, x=0에서 매끄럽게 변하기 때문에 gradient decent에서 수렴 속도가 빠름
👍장점: ReLU + Leaky ReLU 장점
👎단점: exp()에 대한 미분값 계산이 필요해 연산 비용

2. Data Preprocessing
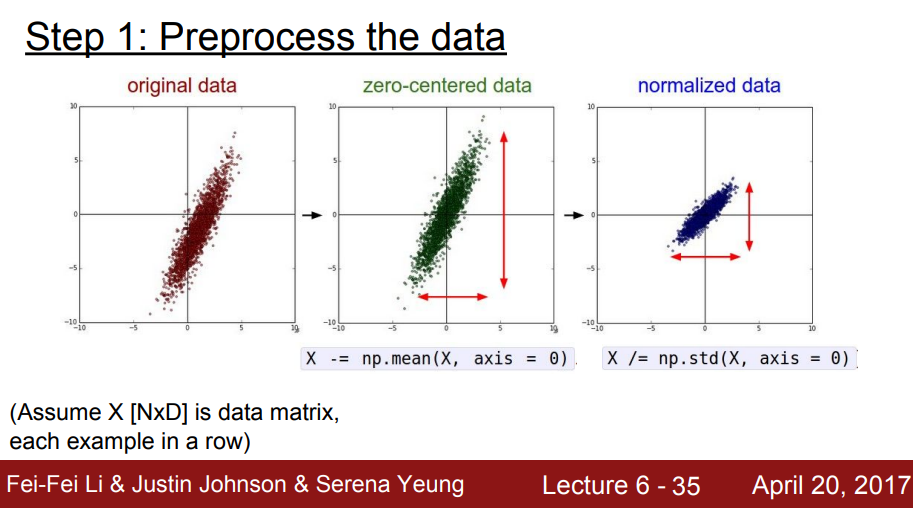
일반적인 머신러닝에서 입력데이터를 전처리하는 과정
zero-centered으로 만들고normalize
앞서 모든 입력 값이 positive일 경우 w가 전부 음수나 양수가 되어서 최적의 weight update를 할 수 없는 문제가 발생한 것을 봤다.
➡️ 입력 값에 zero-mean 값을 빼서 zero-centered로 만들어줘서 해결!
모든 차원이 동일한 범위 안에 있게 해줘서 동등하게 contribute 하기 위해서 normalize를 한다.
이미지 데이터는 픽셀 값이 전부 (0~255)로 같은 범위이기 때문에 normalize가 필요 없다!
➡️ 이미지 데이터에서는
zero-centered로만 만들어준다.
train set과 test set을 전처리할 때는 동일한 mean을 이용해서 zero-mean을 해준다.
➡️ 여기서 mean 값을 채널 전체의 mean으로 할지, 채널마다 독립적인 mean으로 할지는 선택할 수 있지만 큰 차이는 없다.
(AlexNet은 전자, VGGNet은 후자의 방법으로 전처리를 한다.)
3. Weight Initialization
➡️ 모든 뉴런이 같은 값을 output하는 문제 발생! (우리는 뉴런이 다른 값을 학습하길 원함)

w에 작은 랜덤 값을 부여해보자.
정규분포에서 가져온 작은 편차 값들로 w를 initialize해준다.
➡️ layer가 깊어질수록 w initialization에서 작은 값을 주다보니 0으로 수렴하게 된다!
➡️ collapse!
🤔 initialization할 때 w를 너무 작게 하면 (예를 들어 0.01을 곱함) collapse 발생, 너무 크게 하면 (예를 들어 1을 곱함) saturate 된다!
w initialization을 잘하려면 어떻게 해야 할까?
➡️ Xavier initialization (2010)을 살펴보자.
Xavier initialization은 입출력의 분산을 맞춰준다!
➡️ 입력의 수가 적으면 더 작은 값으로 나눠서 좀 더 큰 가중치 값을 얻는다. (입력의 수가 적으면 가중치가 더 커야 출력의 분산만큼 큰 값을 얻을 수 있기 때문)
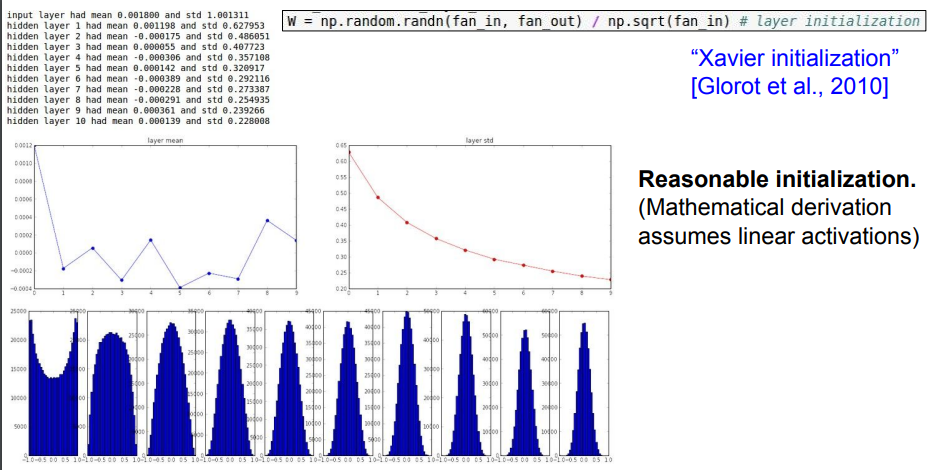
xavier는 위에서처럼 0.01이나 1처럼 고정된 값을 곱하는 게 아니라, 랜덤의 가우시안 분포 값에서 np.sqrt(fan_in)으로 나누어준다!
➡️ 입력 값의 개수에 따라 상대적으로 값을 조절하여 w initialization을 해주기 때문에 고정된 값을 곱하는 것보다 👍
입력 값들의 수가 적으면 w가 커야 하기 때문에 작은 수로 나누어 스케일링해주고, 입력 값들의 수가 많으면 w가 작아야 하기 때문에 큰 수로 나누어 스케일링
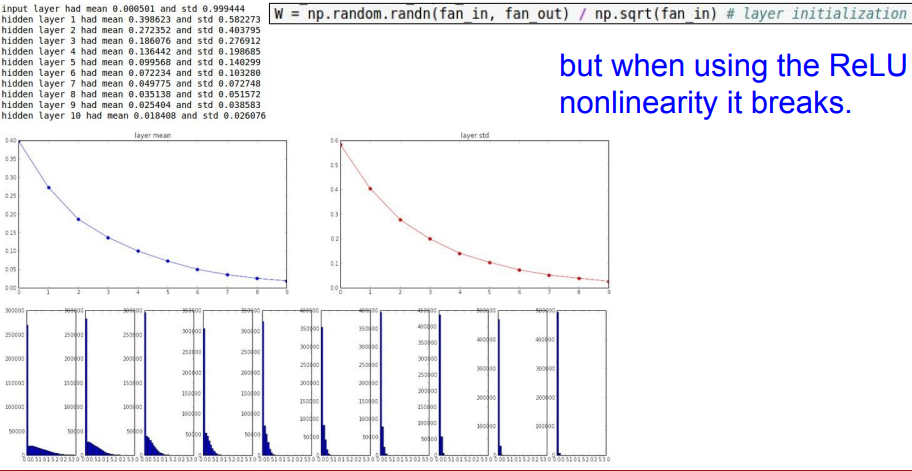
그런데 비선형함수인 ReLU를 이용하면 문제가 생긴다.
zero-mean 함수였던 tanh와 다르게 ReLU는 음수 부분이 전부 0이 되기 때문에, ReLU를 지나면서 편차가 절반이 되고 layer가 깊어질수록 std가 0이 된다.
여기서 std는 standard deviation (표준 편차)
🤔 출력 값에 0이 많으면 w의 업데이트는 잘 이루어지지 않는다.
➡️ 아래와 같이 np.sqrt(fan_in/2)로 수정해서 해결!
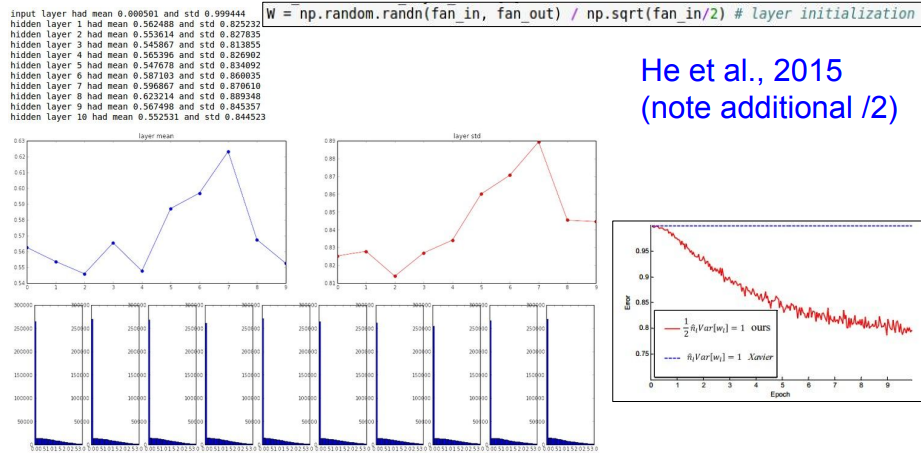
➡️ 뉴런 중 절반이 죽는다는 걸 고려해서 2로 나눠주는 것!
작은 변화에도 학습에 있어서 엄청난 차이를 가져올 수 있다!
4. Batch Normalization

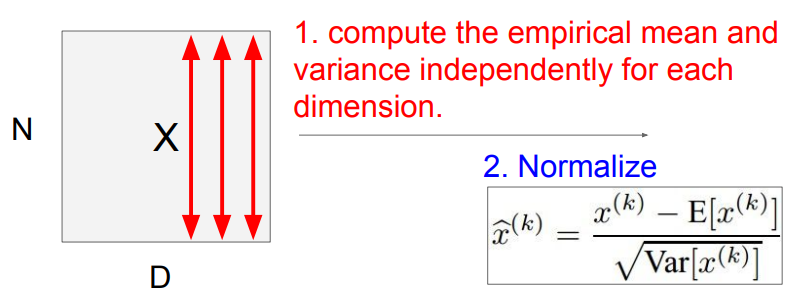
batch 단위로 한 레이어에 입력으로 들어오는 모든 값들을 이용해서 평균과 분산을 구한다.
평균과 분산값을 이용해 Narmalization을 해준다.
Batch norm은 미분이 가능한 함수!
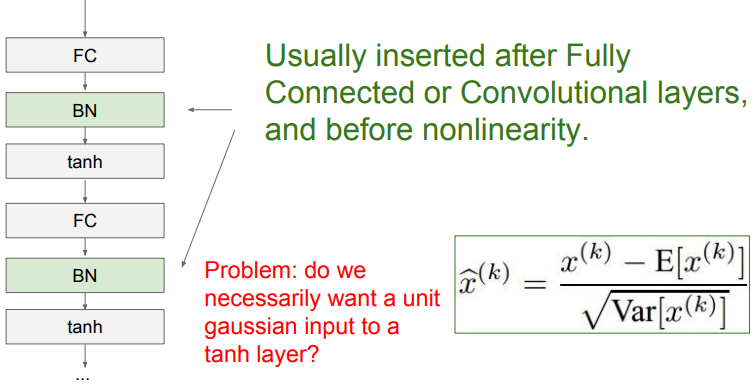
Batch 연산은 FC나 Conv 직후에 넣어준다.
5. Babysitting the Learning Process
- Network architecture를 어떻게 구성해야하는지
- 학습과정을 어떤 시각으로 바라봐야하는지
- 하이퍼파라미터를 어떻게 조정해야하는지
-
데이터 전처리
-
network architecture 구성
-
loss 함수 지정 or regularization
-
training
- sanity check으로 먼저 진행
- train set에서 일부만 가져와서 시작한 후, 과적합이 되면 학습이 잘 되는 걸 확인
- sanity check으로 먼저 진행
-
전체 데이터 학습
- Loss 확인하면서 learning rate 조정
