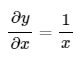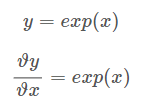소프트맥스 함수와 교차 엔트로피 오차의 계산 그래프를 그려보고, 그 역전파를 구해보자!
- 소프트맥스 함수:
Softmax계층- 교차 엔트로피 오차:
Cross Entropy Error계층- 둘을 조합한 계층:
Softmax-with-Loss계층
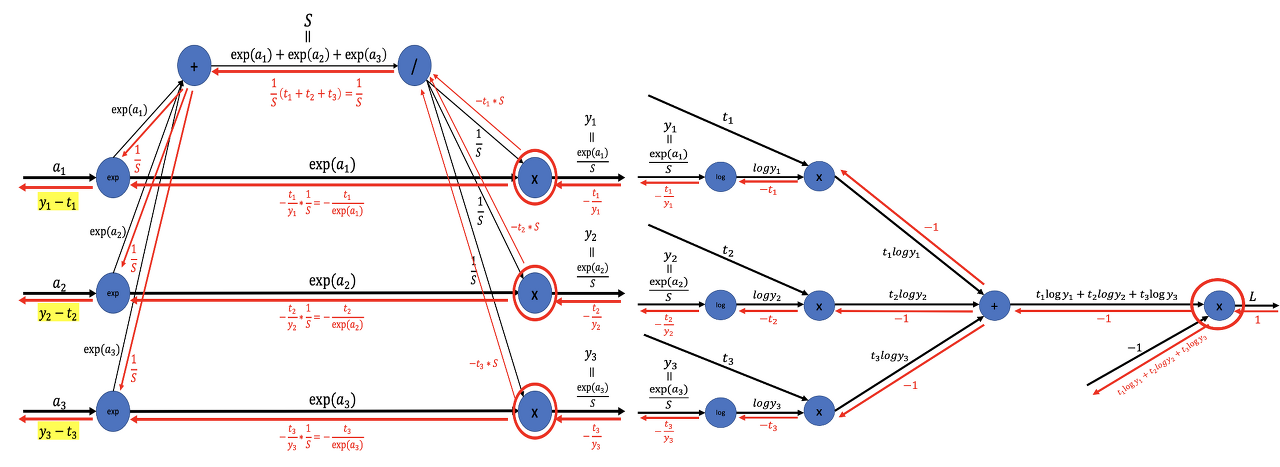
결과를 먼저 보면 Softmax-with-Loss 계층의 계산 그래프는 아래와 같다.
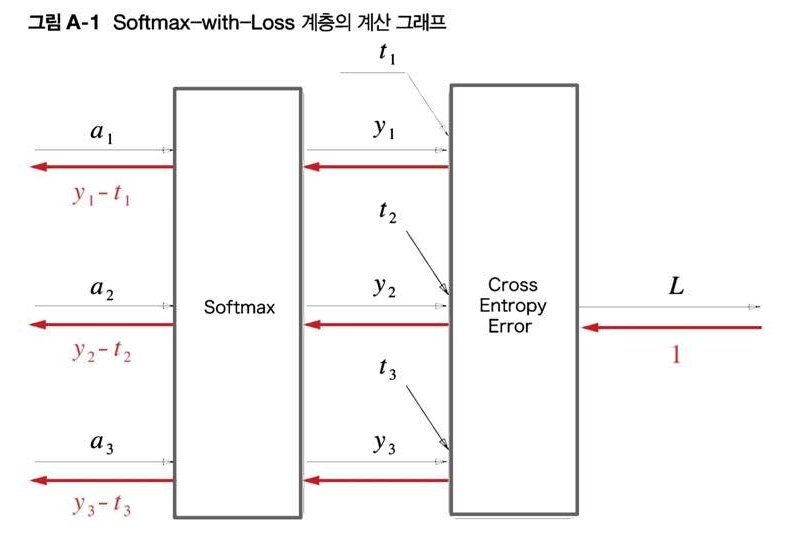
위의 그림에서는 3클래스 분류를 수행하는 신경망을 가정하고 있다.
(a₁, a₂, a₃): 이전 계층으로부터의 입력(y₁, y₂, y₃): Softmax 계층의 출력(t₁, t₂, t₃): 정답 레이블손실 L: Cross Entropy Error 계층의 출력
➡️ Softmax-with-Loss 계층의 역전파 결과는 (y₁ - t₁, y₂ - t₂, y₃ - t₃)
1. 순전파
Softmax 계층과 Cross Entropy Error 계층을 살펴보자!
1-1) Softmax 계층의 순전파
Softmax 함수의 수식은 아래와 같다.
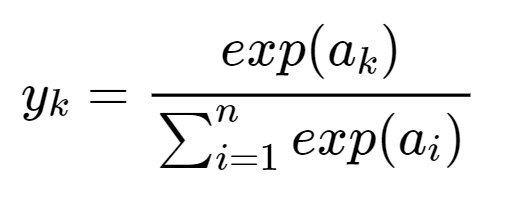
Softmax 계층의 계산 그래프는 아래와 같다.
S: 지수의 합(분모 항)(y₁, y₂, y₃): 최종 출력
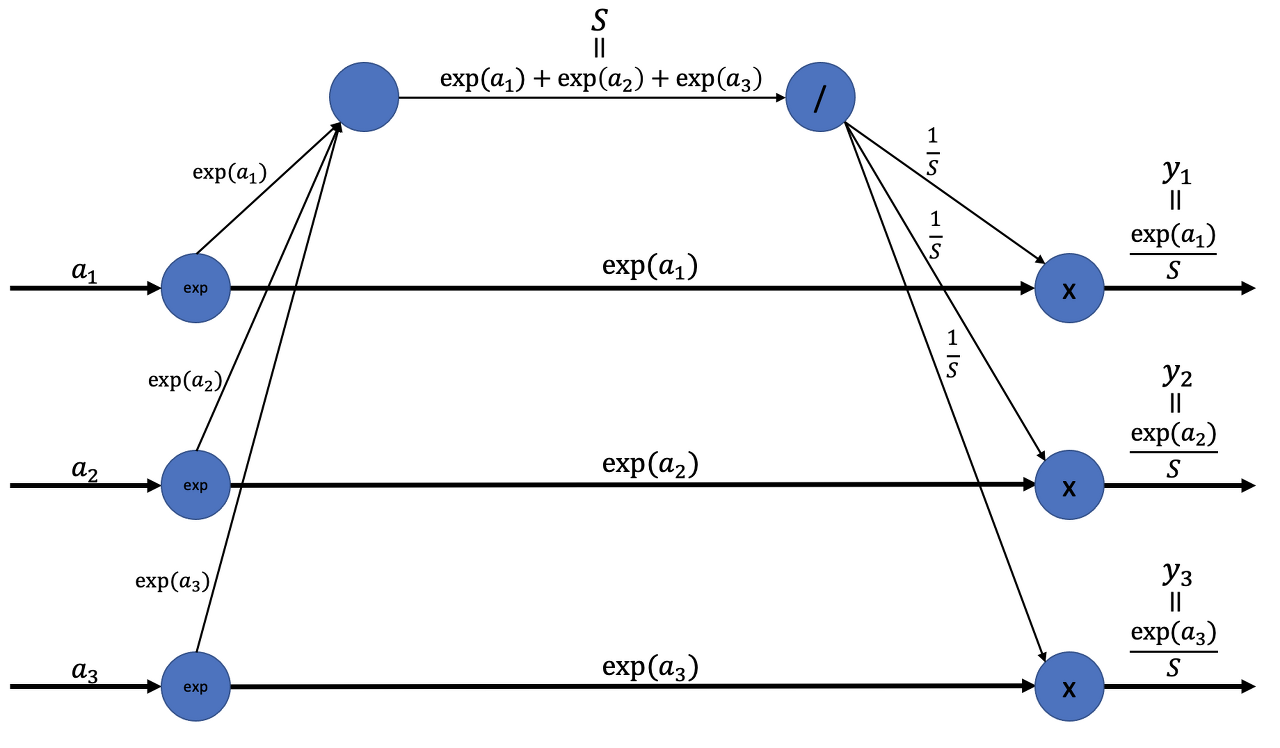
1-2) Cross Entropy Error 계층의 순전파
교차 엔트로피 오차의 수식은 아래와 같다.
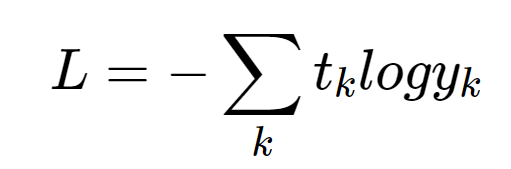
교차 엔트로피 오차의 계산 그래프는 아래와 같다.
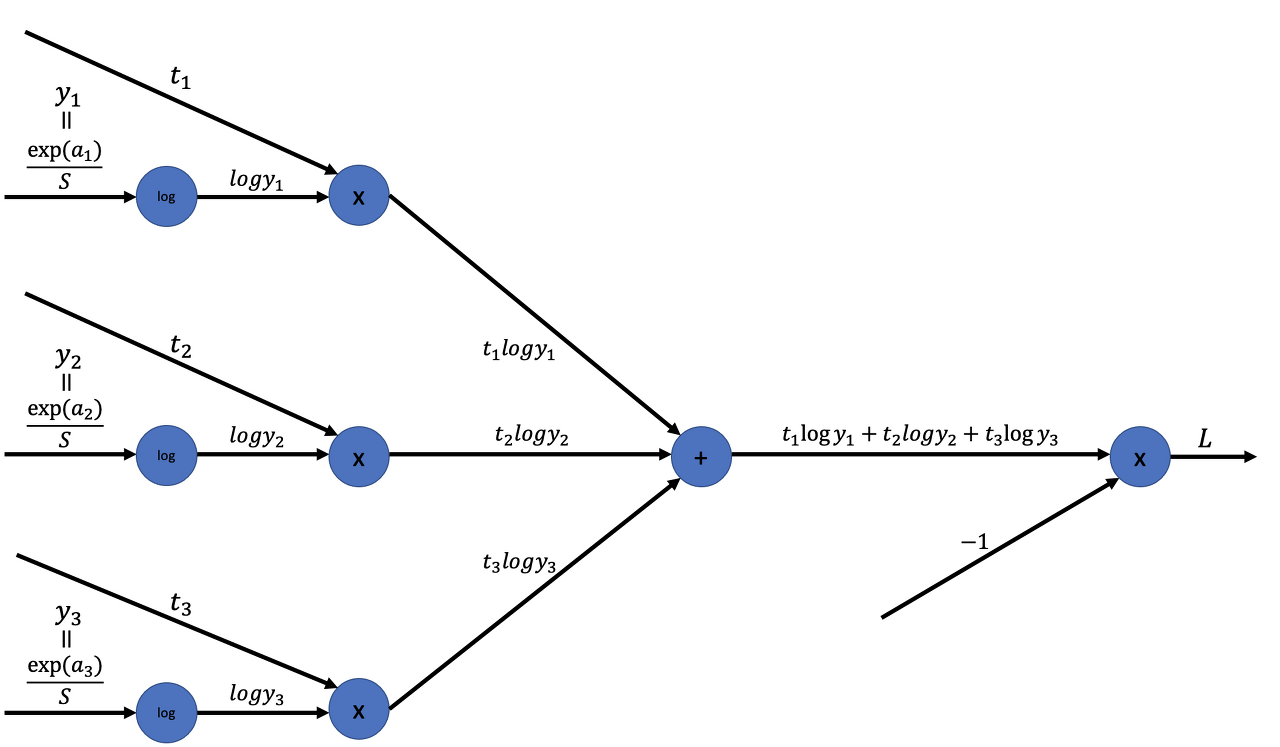
2. 역전파
2-1) Cross Entropy Error 계층의 역전파
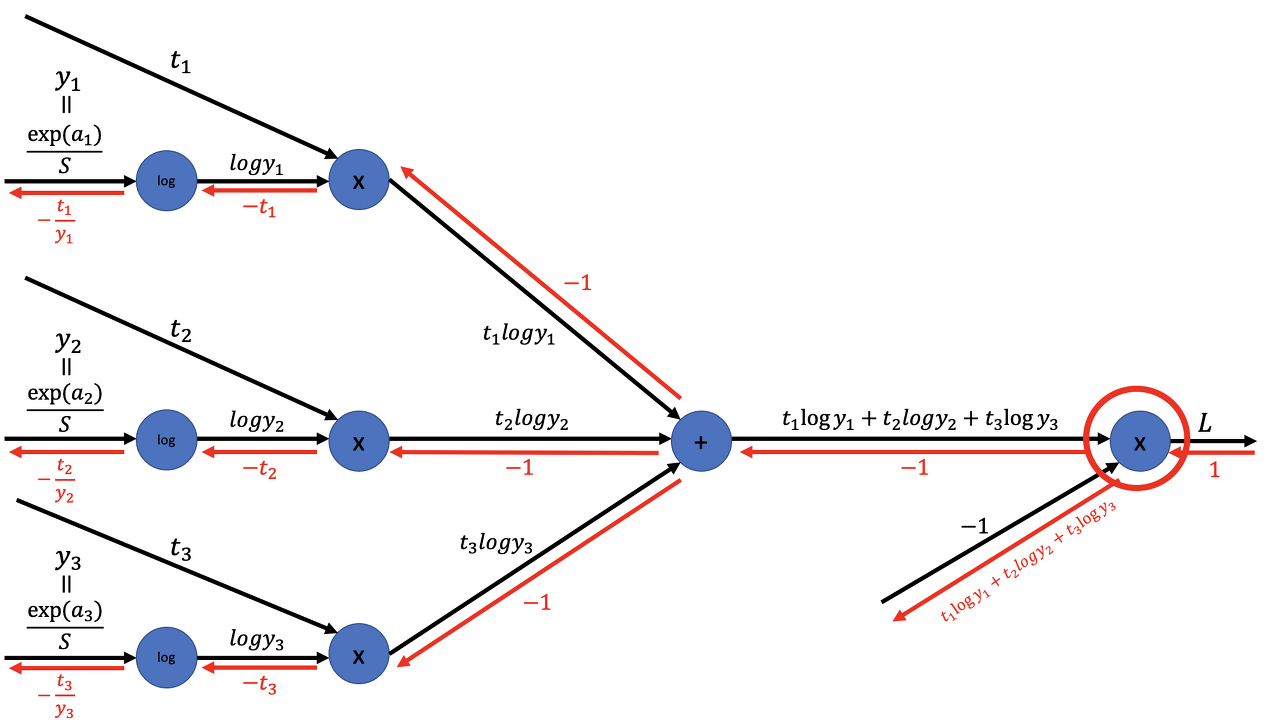
- 역전파의
초깃값(가장 오른쪽 역전파의 값)은 1x노드의 역전파는 순전파 시의 입력들의 값을 "서로 바꿔" 상류의 미분에 곱하고 하류로 흘린다.+노드의 역전파는 상류에서 전해지는 미분을 그대로 흘린다.log노드의 역전파는 아래와 같다.
결과는 (-t₁/y₁, -t₂/y₂, -t₃/y₃)
➡️ Softmax 계층으로의 역전파 입력
2-2) Softmax 계층의 역전파
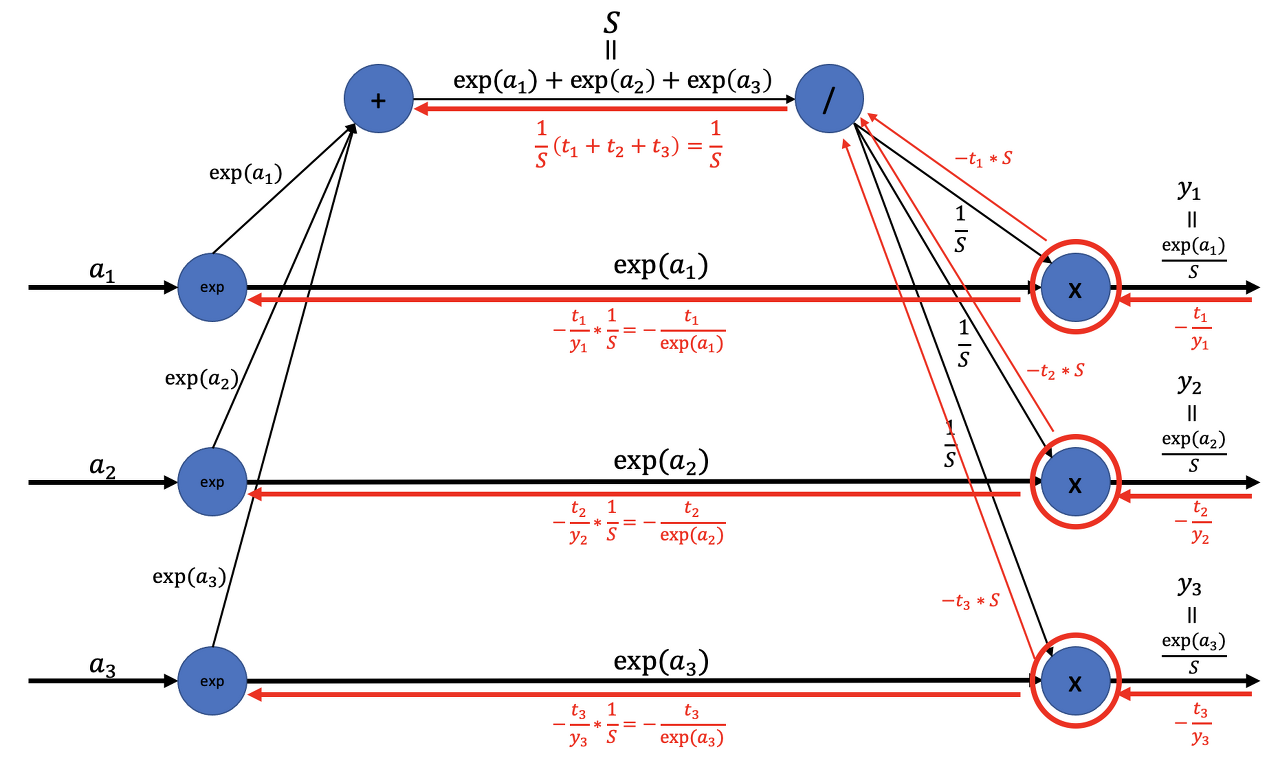
순전파 때 여러 갈래로 나뉘어 흘렸다면 역전파 때는 그 반대로 흘러온 여러 값을 더한다.
이 더해진 값이 / 노드의 역전파를 거쳐 (t₁ + t₂ + t₃)/S = 1/S가 된다. 여기에서 (t₁, t₂, t₃)은 '원-핫 벡터'로 표현된 정답 레이블이다.
원-핫 벡터란 (t₁, t₂, t₃) 중 하나만 1이고 나머지는 전부 0임을 뜻한다. 따라서 t₁ + t₂ + t₃ = 1
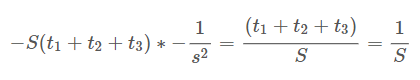
/노드의 역전파는 '상류에서 흘러온 값'에 '순전파 때의 출력을 제곱한 후 마이너스를 붙인 값'을 곱해 하류로 전달한다.
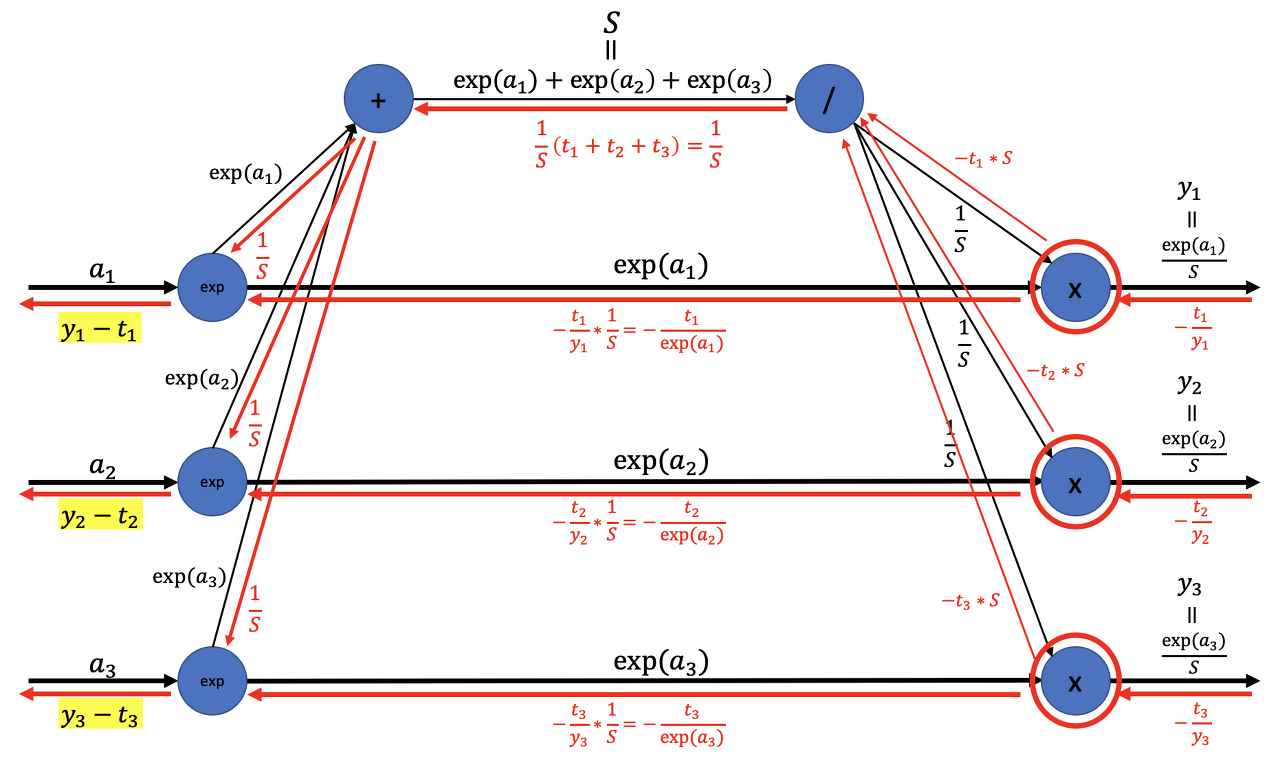
exp노드에서는 다음 관계식이 성립한다.
exp 노드에서 역전파는 두 갈래의 입력의 합에 exp(a₁)을 곱한 값
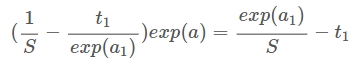
위의 식을 변형하면 y₁ - t₁이 된다.
➡️ 순전파의 입력이 a₁인 첫 번째 노드에서는 역전파가 y₁ - t₁
❗여기에서 다룬 3클래스 분류 외에 n클래스 분류에서도 같은 결과가 유도되는 것은 쉽게 알아낼 수 있다.
3. 정리
여기에선 Softmax-with-Loss 계층의 계산 그래프를 생략 없이 그려가며 그 역전파를 구했다.
Softmax-with-Loss 계층 외에도, 배치 정규화 계층 등 복잡해 보이는 계층을 만나면 앞서 한 방식처럼 계산 그래프로 한 단계식 확인하면서 미분해보기(역전파)!
참고)
https://techblog-history-younghunjo1.tistory.com/376?category=1021615
https://bbooo.tistory.com/18