CNN (3)

1. 딥러닝의 “더 깊게 쌓기” 흐름과 한계

• CNN은 점점 더 깊은 구조로 발전해왔고, 깊이(layer 수)가 증가할수록 모델의 표현력과 성능이 커졌다.
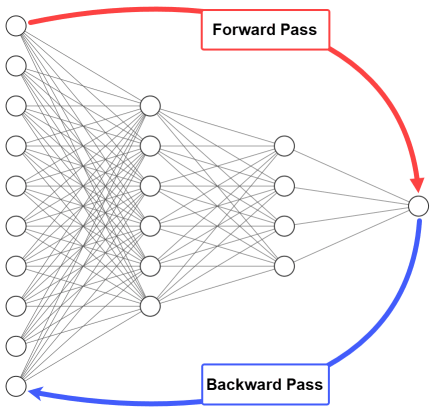
• 하지만 깊이가 깊어질수록 Gradient Vanishing Problem(기울기 소실)이 심화되어, 입력층 근처의 가중치 학습이 원활하게 이루어지지 않았다.
• Gradient Vanishing Problem(기울기 소실)은 과적합과는 달리, Backpropagation 과정 중 작은 gradient가 여러 층에 걸쳐 계속 곱해지며 거의 0에 수렴하는 현상

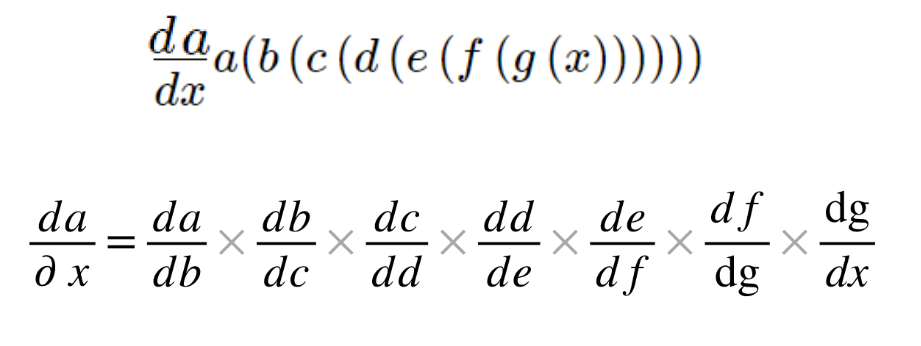
2. ResNet: Skip Connection으로 Gradient Vanishing 극복

• ResNet은 Microsoft 연구진이 개발한 모델로, gradient vanishing 문제를 해결하고 매우 깊은 신경망 구조(예: 152층)를 가능하게 했다.

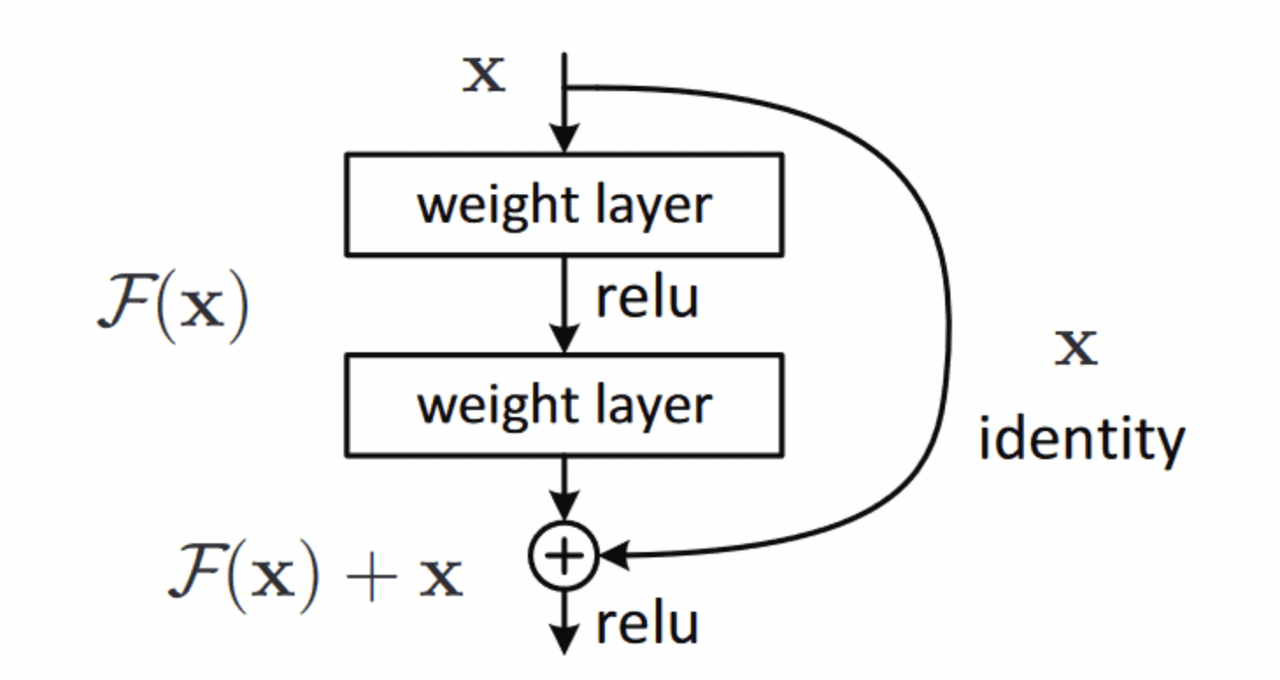
• 핵심은 Skip Connection(잔차 연결) 구조

  • 일반 Forward 연산뿐 아니라, 입력 x를 스킵(skipping)하여 직접 다음 층에 더하고, ReLU를 통과시키는 구조이다: $\mathcal{F}(x) + x$
  • 이렇게 하면 역전파 시 gradient는 $\nabla\mathcal{F}(x) + 1$ 형태로 입력층까지 전달되어, gradient가 0에 수렴하는 것을 막아준다.

• Residual Block이 중첩된 ResNet은 딥러닝 기본 골격으로 자리잡으며 높은 활용도를 보이고 있다.

• 일반적인 신경망 흐름: 보통은 입력 x가 네트워크를 거치면서 변환된 출력 $\mathcal{F}(x)$만 다음 층으로 전달된다.
  $y = \mathcal{F}(x)$

• Skip Connection이 들어가면: ResNet에서는 $\mathcal{F}(x)$에 입력 x를 그대로 더해준다.
  $y = \mathcal{F}(x) + x$

3. DenseNet: Concatenation 기반의 ‘Dense’ 연결

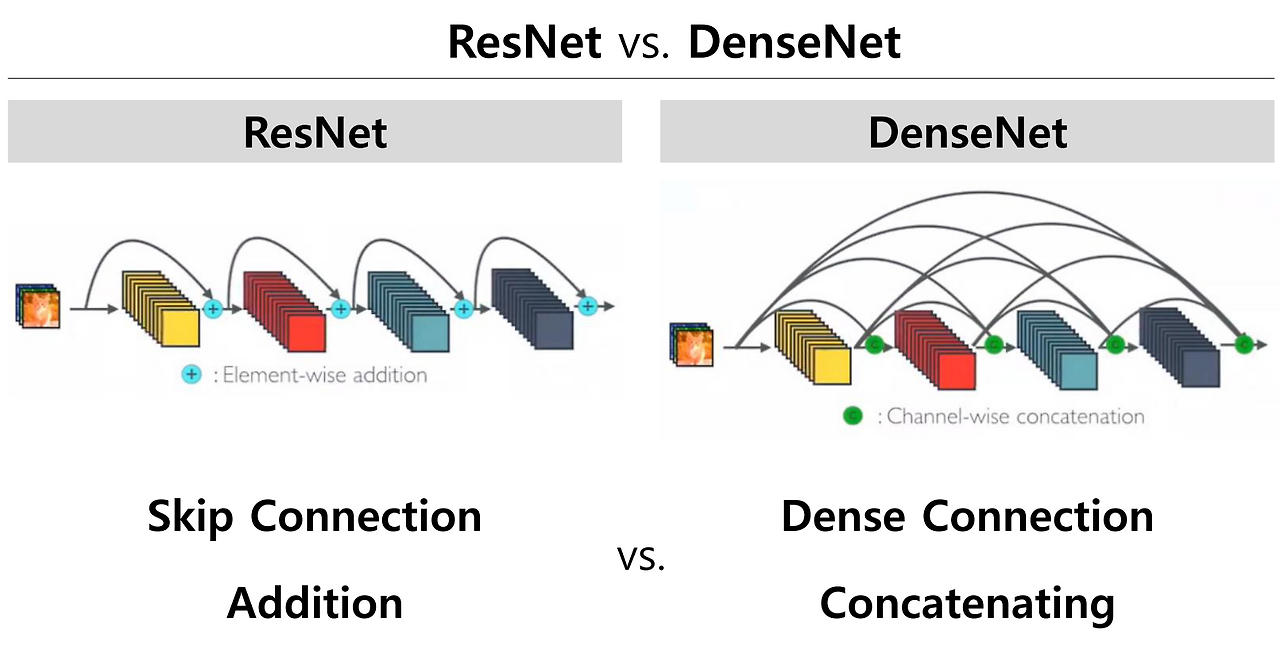
• DenseNet은 ResNet의 구조를 확장해, 각 층의 출력을 덧셈(sum) 방식이 아닌 연결(concatenation) 방식으로 통합한다.

• 이 방식의 장점

  • $\mathcal{F}(x)$의 특징이 $x$로 인해 왜곡되지 않도록 방지
  • 정보의 손실 없이, 모든 층의 정보가 이후 층으로 명확하게 전달됨

• 각 층은 이전 모든 층의 출력을 이어받아, Dense Connection 구조를 이루게 된다.

  • $y = [x, \mathcal{F}_1(x), \mathcal{F}_2(x), \dots]$

• ResNet (덧셈)이라면
  $y = x + \mathcal{F}(x) = [1, 2] + [3, 4] = [4, 6]$

• DenseNet (Concatenation)이라면
  $y = [1, 2] \,||\, [3, 4] \,||\, [5, 6] = [1, 2, 3, 4, 5, 6]$