[BOJ] 26260. 이가 빠진 이진 트리

bbookng·2023년 6월 5일

백준 알고리즘 트리 파이썬

BOJ

목록 보기

2/5

📌 26260. 이가 빠진 이진 트리

오랜만에 트리 문제를 풀었다. 항상 제일 약한 부분이 트리 파트라고 생각해서 이번에 풀면서 개념을 한번 더 잡고자 했다 ! 이번주 스터디 문제인 백준 26260번 이가 빠진 이진 트리 문제이다.

💡 GOLD 5 / 172ms

문제

김소마는 최근에 포화 이진 트리에 대해 배웠다. 포화 이진 트리란, 이진 트리에서 리프 노드를 제외한 모든 노드가 두 자식 노드를 가지며, 모든 리프 노드가 채워진 것을 말한다. 아래의 그림을 통해 쉽게 이해하자.

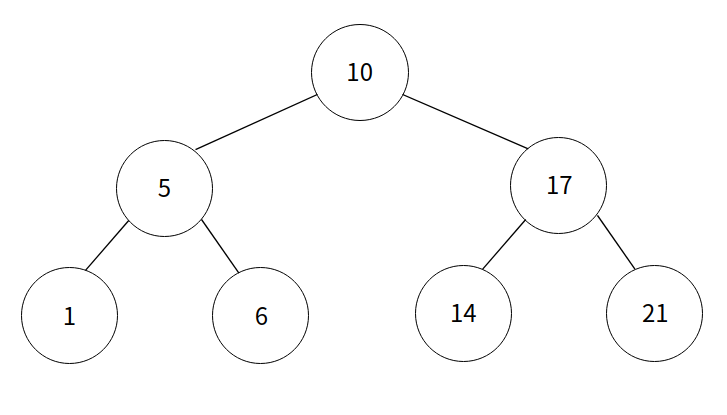
김소마는 예쁜 포화 이진 검색 트리를 그려 만족했지만, 밥 먹다 흘린 소스가 리프 노드 한 개를 가려버렸다. 여기서 이진 검색 트리란, 모든 왼쪽 자식이 자신보다 작고, 모든 오른쪽 자식이 자신보다 큰 이진 트리를 이야기한다.

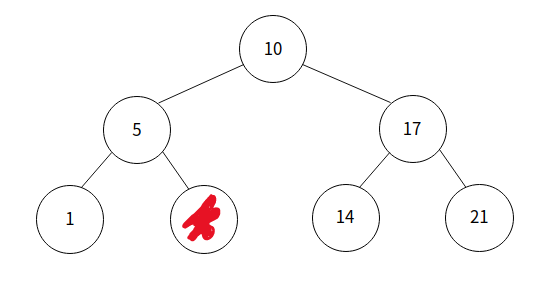
그림을 버리려던 찰나, 김소마는 갑자기 포화 이진 검색 트리를 유지하며, 임의의 수를 넣을 때, 트리 구조가 어떻게 바뀔지 궁금해졌다. 멍청한 김소마를 위해 당신이 도와주자.

입력

첫 번째 줄에 가려진 노드를 포함한 노드의 개수 $N$ 이 주어진다. $(N=2^k-1;$ $2 \le k \le 17;$ $k$ 는 정수 $)$

두 번째 줄에 $A_1, A_2, \cdots, A_N$ 이 공백으로 구분되어 주어진다. $A_i$ 는 $i$ 번 노드에 적혀있는 수이다. $(0 \le A_i \le 10^9;$ 가려진 하나의 노드에 대해서만 $A_i = -1)$
$i \neq j$ 이면 $A_i \neq A_j$ 이다. 노드 번호는 루트 노드부터 시작하여, 같은 깊이 내 왼쪽에서 오른쪽으로 갈수록 증가하는 순서로 매겨진다 (아래 그림 참조).

세 번째 줄에 트리에 넣을 수 $X$ 가 주어진다. $(0 \le X \le 10^9;$ $X \neq A_i)$

입력으로 주어지는 모든 수는 정수이다.

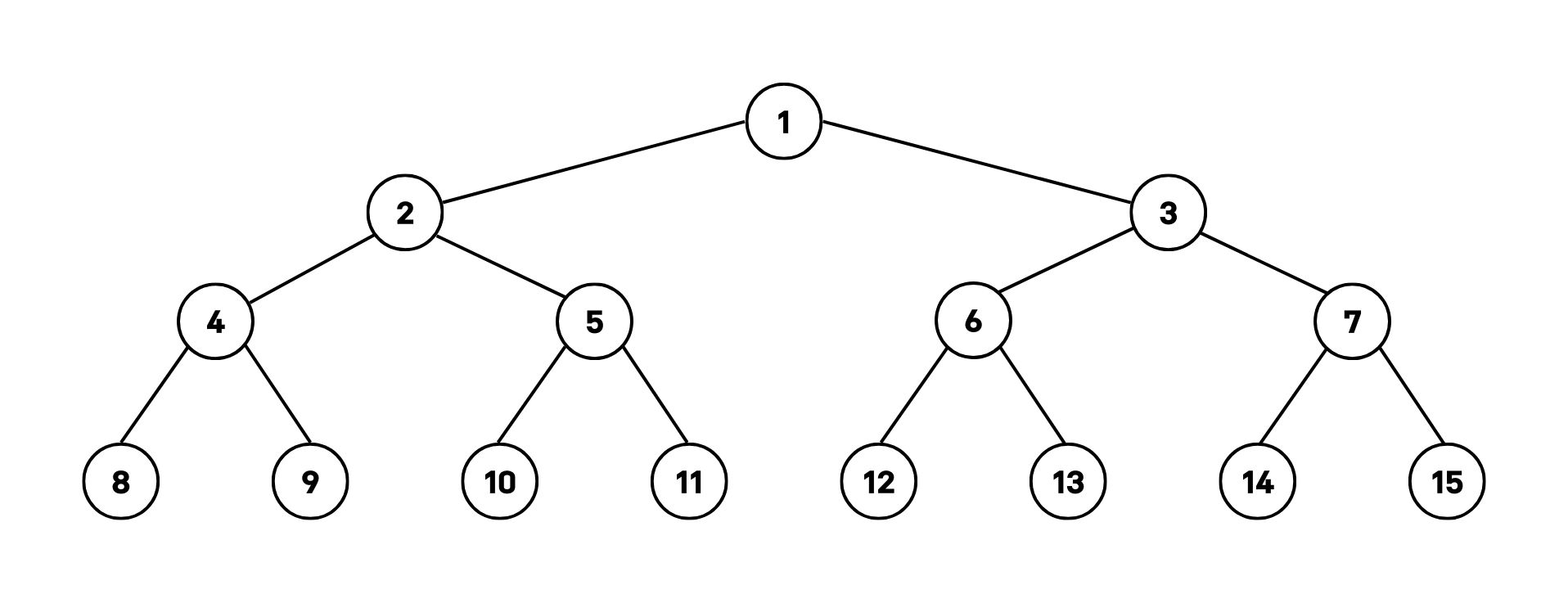
출력

첫 번째 줄에 바뀐 트리를 후위(postorder) 순회한 결과를 출력한다. (단, 왼쪽 자식 노드를 먼저 방문한다.)

예제 입력

7
10 5 17 1 -1 14 21
18

예제 출력

1 10 5 17 21 18 14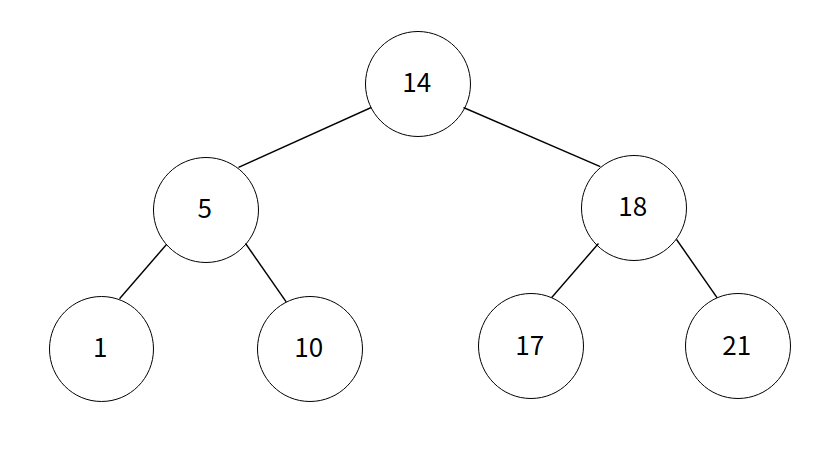

💡 PS

입력을 받은 후 -1 의 인덱스를 찾아 X로 바꿔준다.
오름차순으로 정렬을 한다.
노드마다 왼쪽 자식과 오른쪽 자식이 있는지 검사하고, 있다면 계속 재귀해서 들어가는 함수를 작성한다.
후위순회 코드로 왼쪽 자식 노드부터 차례대로 출력하게 해두었고, 가장 마지막 레이어에 있는 리프 노드들은 다시 재귀로 들어가지 않아 출력되지 않기 때문에 거리가 0인 노드인 경우 조건도 추가해주었다.
코드는 다음과 같다.

N = int(input())

nodes = list(map(int, input().split()))
X = int(input())

nodes[nodes.index(-1)] = X
nodes.sort()


def solution(n, d):
    if not d:
        print(nodes[n], d)
        return
    # 왼쪽 자식 노드가 있는지 확인
    if nodes[n - d]:
        solution(n - d, d//2)
    # 오른쪽 자식 노드가 있는지 확인
    if nodes[n + d]:
        solution(n + d, d//2)
    print(nodes[n], d)

solution(N // 2, (N+1)//4)

제출했더니 틀렸다 .. !!!!!

정석대로 풀어봐야 하나 ? 싶어서 싸피 1학기 알고리즘 수업때 배웠던 기억을 더듬어 노드 클래스를 만들고, 이진 탐색 트리를 만드는 코드로 후위순회 하도록 다시 작성하였다.

N = int(input())

nodes = list(map(int, input().split()))
X = int(input())

nodes[nodes.index(-1)] = X
nodes.sort()

# 노드 클래스
class Node:
    def __init__(self, data):
    	# 해당 노드의 값
        self.data = data
        # 왼쪽 자식 노드
        self.left = None
        # 오른쪽 자식 노드
        self.right = None

# Binary Search Tree 구현 함수
def BST(nums):
	# 빈 리스트가 들어오면 더 이상 자식 노드가 없다는 뜻
    if not nums:
        return None
	
    # 중간 값이 노드의 값이 된다.
    mid = len(nums) // 2
    # 각 노드 클래스 생성
    root = Node(nums[mid])
	
    # 자식 노드 값 할당
    root.left = BST(nums[:mid])
    root.right = BST(nums[mid + 1:])

    return root

# Binary Search Tree 
tree = BST(nodes)

# 위 트리를 후위순회 하는 함수
def postorder(root):
	# 노드의 값이 있으면 
    if root:
    	# 왼쪽 자식 노드 부터 
        postorder(root.left)
        postorder(root.right)
        print(root.data, end=' ')

postorder(tree)

위와 같이 통과는 되었다 !

근데 똑같이 정렬된 리스트로 해서 후위순회를 하면 분명 맞을텐데 처음 제출했던 코드가 왜 안됐을까 싶어서 다시 봤다.
오류가 있었다 !!! if nodes[n - d]:, if nodes[n + d]: 해당 조건이 잘못되었다. 이와 같은 조건들을 걸게 되면 노드가 존재하지 않을 경우 뿐만 아니라 노드의 값이 0 일 경우에도 통과하지 않는다는 것이었다.
해당 조건을 빼고 다시 그냥 후위 순회 코드처럼 작성해주었다.
난 바보였나 ...? 그냥 후위순회 코드가 사실 첨에 생각이 안났다.

N = int(input())

nodes = list(map(int, input().split()))
X = int(input())

nodes[nodes.index(-1)] = X
nodes.sort()

def solution(n, d):
    if not d:
        print(nodes[n], end=' ')
        return
    solution(n - d, d//2)
    solution(n + d, d//2)
    print(nodes[n], end=' ')

solution(N // 2, (N+1)//4)

위와 같이 조건만 뺀 코드를 다시 제출하니
클래스로 구현한 것 보다 메모리와 시간 효율성이 좋은 정답이 떴다.

📌 회고

전위순회, 중위순회, 후위순회의 개념에 대해 오랜만에 상기시켜 준 문제였다.
파이썬으로는 알고리즘만 풀기 때문에 객체 지향 개념을 많이 적용하지 않았었는데, 이번에 오랜만에 클래스를 쓰면서 다시 객체에 대해 생각해볼 수 있는 기회가 되었던 것 같다.
처음에 후위순회 코드를 제대로 못짜서 돌고 돌았다. 트리를 순회하는 코드가 머리에 제대로 남아있었다면 헤매지 않았을텐데,, 여기서 얻은 교훈은 그래서 한 번 공부할 때 제대로 개념을 잡고 가자! 이다.

bbookng

이전 포스트

[BOJ] 1253. 좋다

다음 포스트