10진 소수 2진 표기

https://gsmesie692.tistory.com/94
위 글은 부동소수점에 대해 이해하기 쉽게 설명해준다.

• 위 글 요약
  • 10진법 소수를 2진법으로 변환하는 방법
    • ex) 7.625(10) -> 111.101(2)
  • 고정소수점 설명
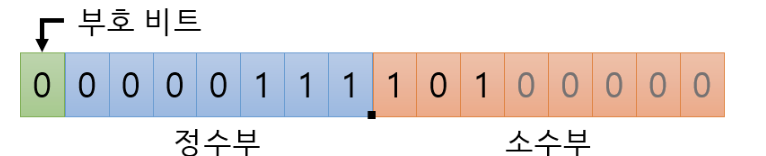
    • ex)
  • 정규화 설명
    • ex) 111.101(2) -> 1.11101 * 2^2(2)
  • 부동소수점 설명
    • ex) IEEE 표준에 따르면 저 부분에는 지수를 그대로 입력하지 않고, 'bias' 라고 하는 지정된 숫자 127(10)를 더한 다음 넣어야 한다.

이 때 10진법으로 표시된 소수를 2진법으롤 바꾸는 테크닉이 소개되는데 이 글에서는 그 테크닉에 대한 증명을 하려고 한다.

위 내용은 앞서 말한 글에서 나오는 내용이다. 요약하자면 2배 씩 곱하면서 일의 자리 숫자를 빼내어 순서대로 나열하는 것이다. 이에 대한 증명은 다음과 같다.

증명

Fact 1. 1 (10) === 1 (2)

Fact 2. x < 1 => 2x < 2

위 두 가지 Fact를 사용하면 10진법으로 표현된 어떠한 소수를 2로 곱한다 해도 일의 자리는 1을 넘을 수 없으며, 1이 된다면 그 것은 2진법의 1과 동일하다. 따라서 해당 수를 2진법으로 변환한다하여도 일의 자리 숫자(0 or 1)는 2진법표기에서도 그대로 표기될 수 있는 것이다.

Fact 3. n진법의 수 m에 n을 곱하는 것은 m의 각 자리의 숫자에 대해 자릿수를 모두 1만큼 증가시킨다.

이제 Fact 3 까지 이용하면 10진법의 수를 2씩 계속 곱하는 것은 해당 수를 2진법으로 변환했을 때 한자리씩 계속 왼쪽으로 이동시키는 작업이라는 것을 이해할 수 있다. 위에서 도출한 내용을 함께 적용하면 증명이 끝난다.

0.1 + 0.2 !== 0.3 ???

이제 적용해서 0.1(10)과 0.2(10) 을 이진법 수로 바꿔보자.

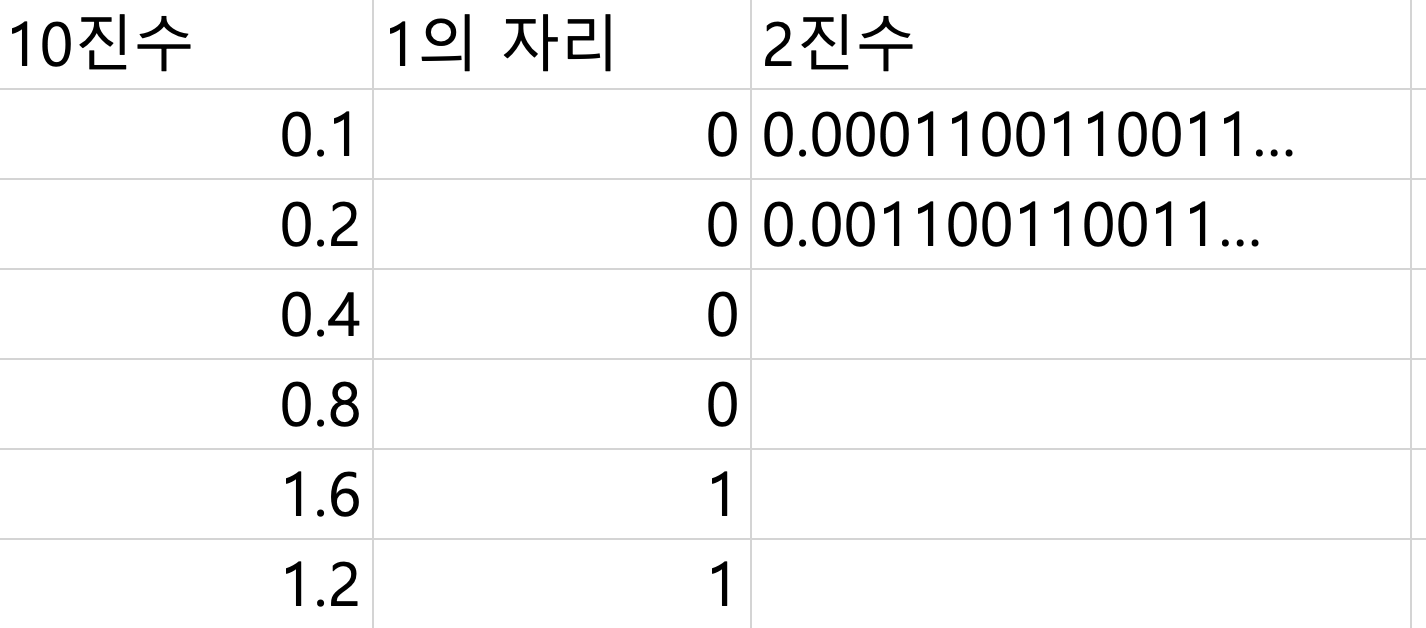
결과는 위와 같다. 무한 소수다. 부동 소수점은 진수부와 가수부로 나눠서 숫자를 표기하는 방법인데, 무한 소수의 경우 가수부가 무한하다. 컴퓨터는 숫자를 표현하는데 유한한 비트를 사용하기 때문에 부동소수로 0.1을 표현하지 못한다는 것은 이와 같은 이유에서이다. 따라서 0.1을 컴퓨터는 rounding하여 표현하고 0.2 또한 마찬가지일 거이며, 이 두 값을 더한 값은 0.3과는 당연하게 오차가 발생할 수 있기에 0.1 + 0.2 !== 0.3이 true인 현상이 나타나는 것이다.