Kernel이란?

PCA, SVM 등에서 사용되는 커널(kernel) 기법은 비선형 함수인 커널함수를 이용하여 비선형 데이터를 고차원 공간으로 매핑하는 기술입니다.

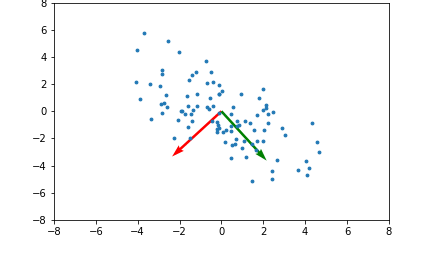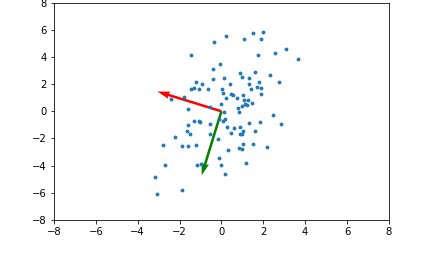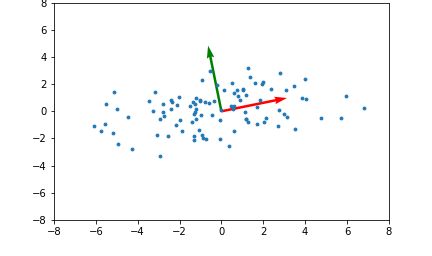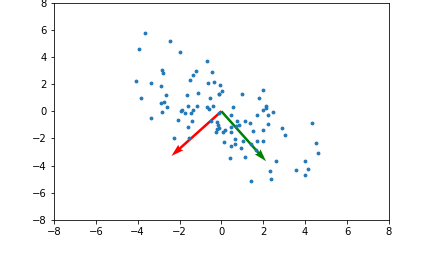
아래 좌측의 데이터 분포를 보면 어떠한 방향으로의 선형변환으로도 데이터 분포를 잘 분류할 수 없을 것 입니다.

그러나 이를 커널함수를 이용해 고차원 공간으로 매핑하여 PCA를 수행한다면 데이터 분포를 분류할 수 있는 결정 공간을 찾을 수 있게 됩니다.

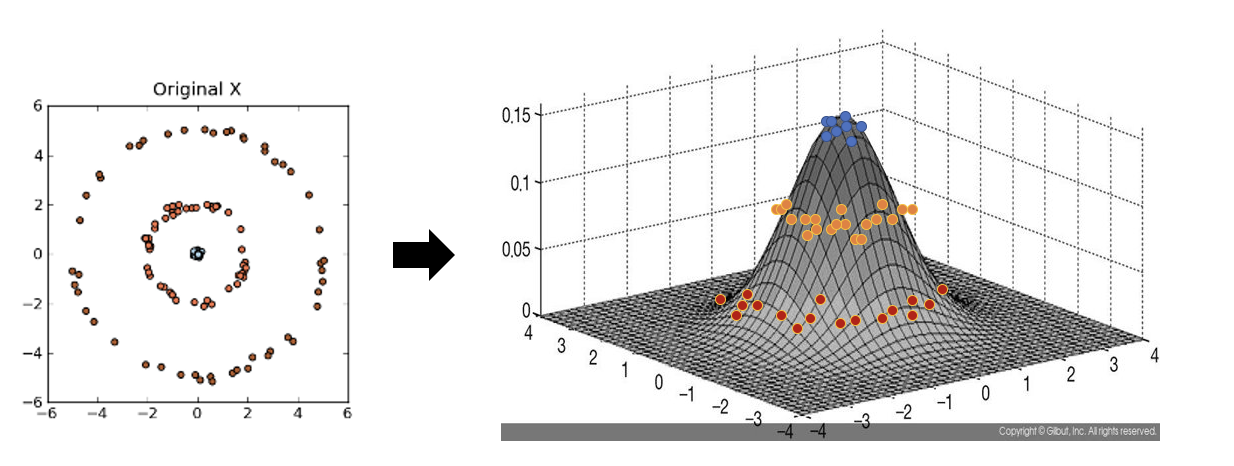
커널 PCA를 사용한 비선형 매핑

여태까지 많은 머신 러닝 알고리즘은 입력 데이터가 선형적으로 구분이 가능하다는 가정을 합니다. 다른 알고리즘들-아달린, 로지스틱 회귀, SVM-은 선형적으로 완벽하게 분리되지 않는 이유를 잡음때문이라고 이야기합니다.

실전에서는 더 자주 비선형 문제들을 맞닥뜨립니다. 이 경우에 항상 PCA나 LDA와 같은 차원 축소 기법이 최선이라고는 말할 수 없겠죠. 이제부터 알아볼 것은 PCA의 커널화 버전인 KPCA입니다.

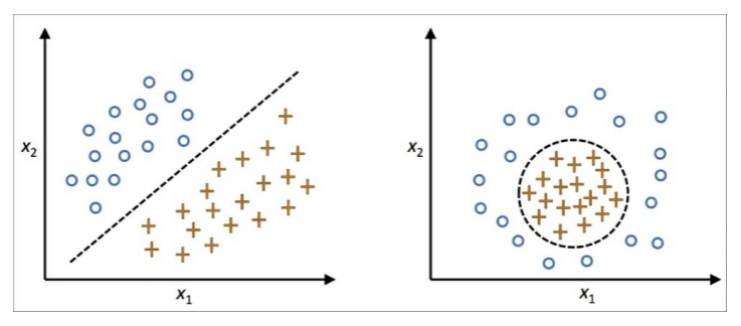
kernel function

이름만 봐서는 매우 어려워 보이지만, kernel function은 단순히 두 개의 벡터를 입력으로 가지는 함수이다. 그리고 일반적으로 두 벡터 사이의 거리 (보통, 두 벡터의 차의 유클리디안 norm) 에 반비례한다. 기존 formulation의 내적 부분을 이 kernel function을 통해 만든 kernel matrix로 대채하는 것이 바로 Kernel trick이다.

그 의미를 조금 들여다 보면, 우리의 데이터가 살고 있는 n 차원의 유클리디언 공간을 매우 차원이 큰 공간으로 mapping하는 nonlinear function이 있다고 가정하는 것이다.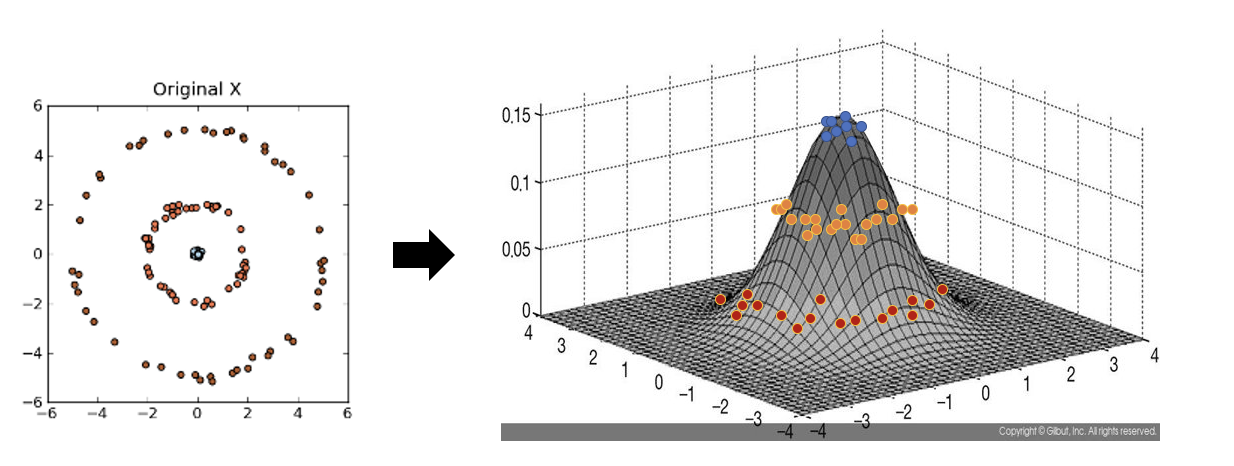

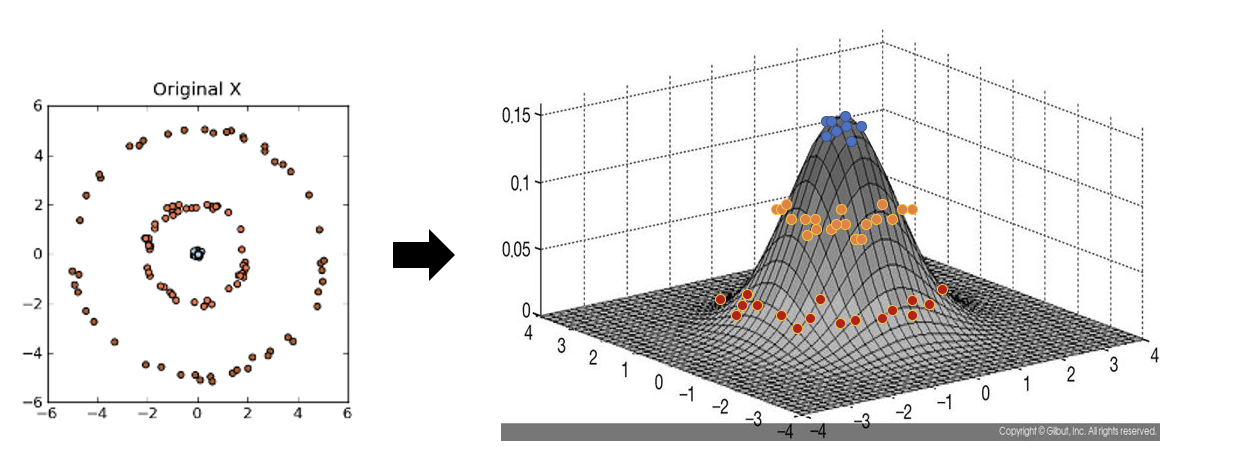
그리고, 그 공간에서 내적은 우리가 정의한 kernel function의 출력값이 된다고 가정하는 것이다.

이번 포스팅의 주제인 Kernel PCA 역시 기존의 PCA에 Kernel trick을 적용한 것이다. PCA를 unsupervised learning에 적용할 경우, 주어진 데이터를 우리가 정한 basis에 projection시키고, 각 basis들에 project된 값이 주어진 데이터의 feature가 되는 구조이다. 이것에 kernel trick을 적용하였기 때문에 기존의 linear projection이 nonlinear한 projection으로 바뀌게 된다.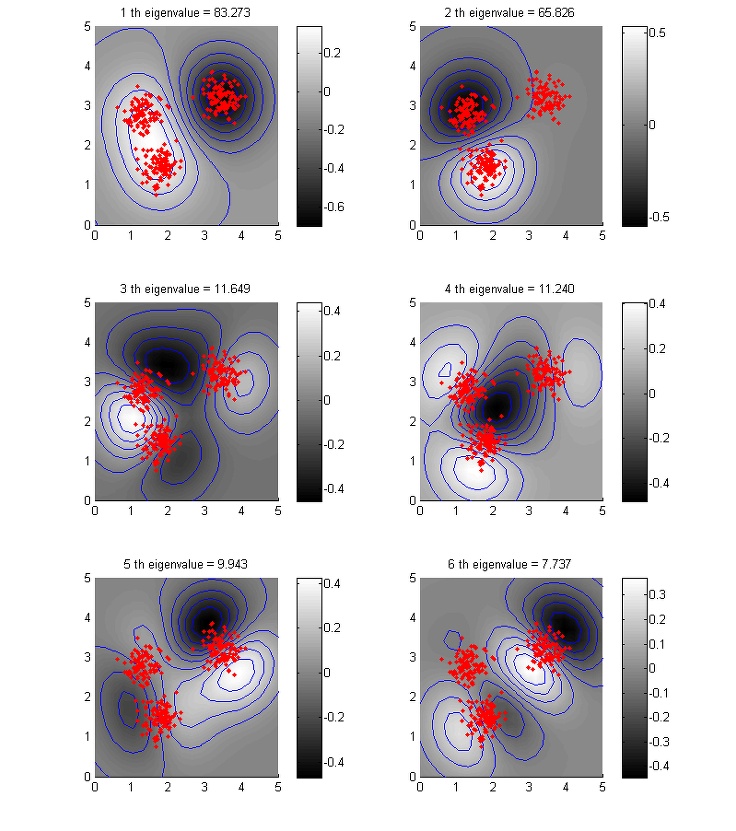
위의 그림은 6개의 feature를 뽑아서 그린 것이고, 아래 그림은 상위 세 개의 feature를 R, G, B에 대응시킨 것이다.

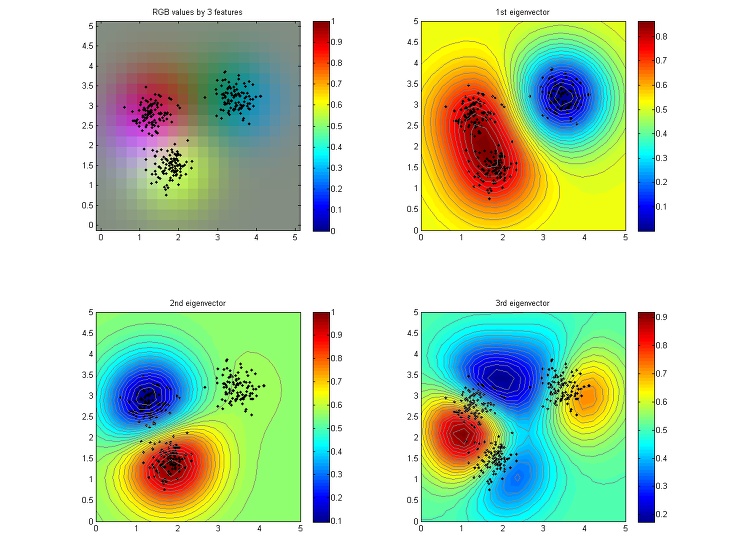
재밌는 점은 원래 데이터의 dimension이 2였는데, kernel PCA를 통해선 그 dimension을 데이터의 갯수에 해당하는 N까지 오히려 올릴 수 있다는 것이다. 이러한 경향은 nonlinear SVM에서도 나타난다.