양치를 하며 문득 들었던 생각이 "나는정말 머신러닝의 기초적인 것들을 다 알고 있기에 모델을 갖고 놀아보는 것인가?"였다. 다소 자조적인 질문일 수 도 있지만, 그 무엇이 '기본'보다 중요할 수 있을까? 당연히 나의 대답은 '아니다'였다. 그렇기에 나는 나 스스로에게 더 떳떳해지기 위해 다시 돌아가 보려 한다. 선 하나가 주었던 설레임을 느꼈던 그날로

Linear Regression

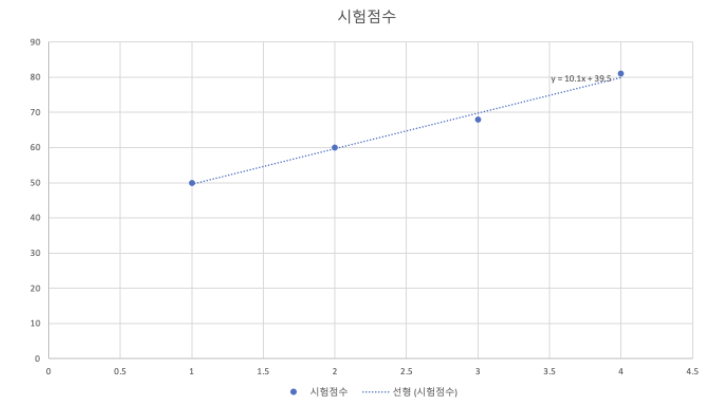
우리는 이 그래프를 보고 가설을 세울 수 있는데, 임의의 직선 1개로 이 그래프를 비슷하게 표현할 수 있다고 가설을 세울 수 있다.

$H(x) = Wx + b$

내가 예시를 들었던 것이 바로 선형회귀에 대한 수식이였다.
우리는 정확한 시험 점수를 예측하기 위해 우리가 만든 임의의 직선(가설)과 점(정답)의 거리가 가까워지도록 해야한다. (=mean squared error를 줄여야 한다.)

$Cost = {{1\over N}\sum_{i=1}^{N}{(H(x_i) - y_i) ^ 2}}$
여기서 우리가 임의로 만든 직선 H(x)를 가설(Hypothesis)이라고 하고 Cost를 손실 함수(Cost or Loss function)라고 한다.

Multi-variable linear regression

선형 회귀와 똑같지만 입력 변수가 여러개라고 생각하면 쉽다. 예를 들어보자

위에서는 마신 커피 잔 수만 입력값으로 들어갔지만 만약 입력값이 2개 이상이 되는 문제를 선형 회귀로 풀고 싶을 때 다중 선형 회귀를 사용하면 되는 것이다!

가설 $H(x_1, x_2, ..., x_n) = w_1x_1 + w_2x_2 + ... + w_nx_n + b$

손실 함수 $Cost = {{1\over N}\sum{(H(x_1, x_2, x_3, ..., x_n) - y) ^ 2}}$