인공신경망, 컨볼루션 신경망, 순환신경망, 자기조직화 지도 이 모든 것들에는 한가지 공통점이 존재하는데 그건 바로 arrow가 존재한다는 것이다 == 방향성 모델이다. arrow는 sum을 구할때 사용되는 매우 중요한 역할을 한다는걸 우리는 알고있다. 하지만 오늘다뤄볼 Boltzmann Machines(이하 BM)은 비방향성 모델이다. 벌써부터 '비방향성' 이라는 단어에 흥미로워질 수 밖에 없다고 생각한다. 그렇게나 중요한 arrows가 없다면 어떻게 작동되는 것일까? 함께 알아보도록 하자.

BM

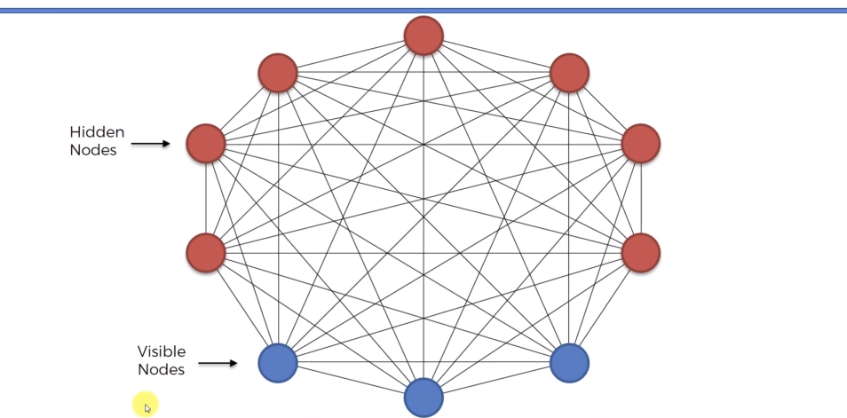
여기 BM의 노드를 표현한 사진이 있다. 우선 은닉노드와 가시적인 노드 를 찾아볼 수 있는데 몇가지 이질적으로 다가오는 것은 바로

'출력 층이 없다'

출력층이 없다는 것은 신경망을 사용할 이유가 없다는 말과 의미가 통한다. 어렵게 설계해둔 신경망에서의 출력을 받아내는 출력층이없다는건 이렇게 유기적으로 노드를 연결시킬 필요성 자체를 의심하게 만든다. 또한,

'층이 없다'

이건 무슨뜻일까? 위의 특징도 출력 층이 없다는 것인데 이는 즉 모든 노드가 모든노드와 연결되어 있다는 뜻으로 귀결된다.

'arrow가 없다'

BM의 가장큰 특징을 위에서도 '비방향성'모델이라고 말하였듯이 BM에는 방향성이 없다. 즉 위의 사진속에서 연결된 노드들 모두 서로 양방향성 즉 '어떠한 방향으로도 이동할 수 있다' 는 것이다.

BM 직관

다른 알고리즘이 '머신'을 만들어 내는게 목표라면 BM은 '시스템'을 만드는 것이 목표라고 할 수 있다. 이를 잘 상기시키면서 BM에대한 직관을 길러보자.

BM 신경망과 시뮬레이티드 어닐링으로부터의 흥미로운 성질들을 결합시킨 모델인데 대규모 병렬처리를 이용하는 강력한 계산 장치이다. BM은 1984년 Geoffrey E. Hinton 과 Terrence J. Sejnowski 에 의해 도입되었다. BM은 커넥셔니스트 (connectionist) 모델로의 최신 접근 방법이다. 이것은 홉필드 모델의 일반화로 여겨질 수 있는데 홉필드 네트워크의 동작 규칙을 확률적인 동작 규칙으로 확장시킨 것으로 생각될 수 있다. 홉필드 네트워크의 동작 규칙에서는 네트워크의 상태를 에너지를 감소시키는 방향으로만 변화시키지만, BM은 에너지가 증가하는 상태의 전이에 대해서도 작은 확률로나마 허용하는 동작규칙을 사용한다.

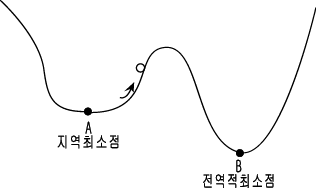
백프로퍼게이션 네트워크를 비롯한 여러 신경망(거의 모든 신경망) 모델들이 지역 최소점 (local minima) 에 빠져서 전역적 최소점 (global minima) 을 구할 수 없는 경우가 빈번한데 비하여 BM은 에너지가 증가하는 방향으로의 전이도 가능하므로 전역적 최소값을 구할 수 있다. 이것의 원리는 마치 그림에서 보는 바와 같이 구슬이 두개의 지역 최소값을 가진 에너지 장벽으로 분리되어 있는 시스템에서 상자를 흔들어 어느 곳으로도 굴러갈 수 있도록 하는 것과 같은 원리인 것이다.

우리가 BM을 학습하는 중요한 이유는 다음과 같다. 우선 이 모델은 탐사, 표현 및 학습 등에 응용될 수 있는 일반적인 접근 방법을 제시해 준다. 또한 이 모델은 엄밀한 수학적인 바탕을 통하여 네트워크의 수렴 성질을 제공하며 지도학습이건 자율학습이건 간에 간단한 학습 알고리즘들을 형성할 수 있게 해 준다. 마지막으로, 이 모델의 단순성으로 인하여 실리콘 칩에 넣는 하드웨어의 구현이 비교적 쉽다는 것이다. BM은 유니트들이 그들의 상태전이를 국부적으로 평가하기 때문에 병렬처리를 쉽게 해준다. 더군다나 BM은 전체적인 구성을 분산 표현하기 때문에 전통적인 컴퓨터 아키텍처를 사용할 때 생길 수 있는 폰 노이만의 병목 현상 (bottleneck) 을 겪지 않는다. .......... BM의 유용한 응용분야로는 VLSI 의 배치문제나 순회판매원 문제 (traveling salesman problem), 최적화 문제의 근사해를 구하는 경우 등에 특히 적합하다.