지금은 2D지도뿐만 아니라 3D지도가 보편화 되어있지만, 2D지도를 생각해 보자. 실제 거리에는 높이가 다른 건물, 복잡한 골목길, 서로 다른 모습을 하고있는 모든 구조물 까지 실제로는 2D지도(종이지도)에 그려진것처럼 정적이지 않다는걸 우리는 모두 알고있다. 하지만 종이지도만 있어도 많은 사람들은 길을 찾을수 있다. 우리가 살고있는 현실의 차원을 그대로 모두 종이지도에 적는다면 사람들은 오히려 더 헷갈리지 않을까? ex)높이가 1.32m인 빨간우체통옆에서 좌회전 하세요. 우리는 단순히 위에서 내려다본 2D지도만 있어도 충분히 원하는 목적지를 찾아갈 수 있다. 나의 비유가 적절했다면, 그래서 어느정도 납득이 되었다면 우리는 SOM을 모두 안것이라 할 수 있다. SOM은 현실에서 길을찾기위해 그려둔 종이지도이기 때문이다.

SOM이란?

차원축소(dimensionality reduction)와 군집화(clustering)를 동시에 수행하는 기법인 자기조직화지도(Self-Organizing Map, SOM)이다.
조금더 풀어서 설명을 해보자면 , 사람이 눈으로 볼 수 있는 저차원(2차원 내지 3차원) 격자에 고차원 데이터의 각 개체들이 대응하도록 인공신경망과 유사한 방식의 학습을 통해 군집을 도출해내는 기법이다. 고차원의 데이터 원공간에서 유사한 개체들은 저차원에 인접한 격자들과 연결된다. 저차원 격자에서의 유사도는 고차원 입력 공간에서의 유사도를 최대한 보존하도록 학습된다.

SOM 아키텍처의 핵심은 대략 아래 그림과 같다.

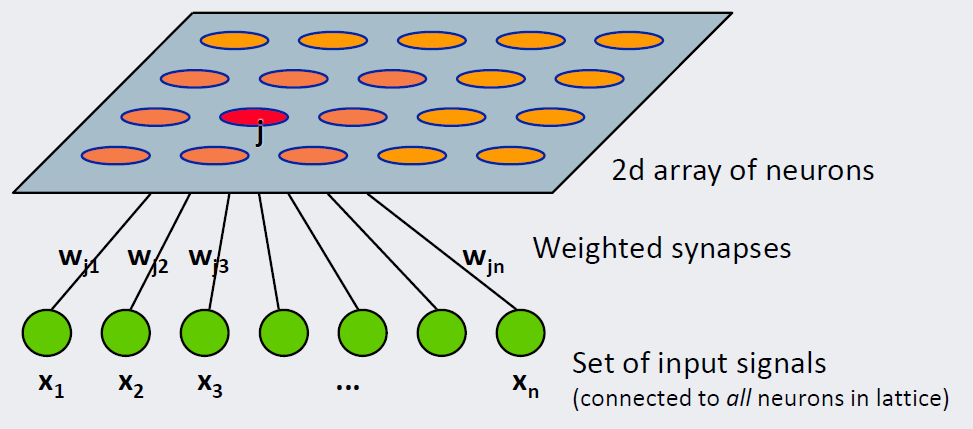
위 그림에서 초록색 노드(xi)는 n차원 입력벡터의 각 요소를 뜻한다. 주황색 노드(wj)는 2차원 격자이다.

저차원 격자 하나에는 여러 개의 입력벡터들이 속할 수 있습니다. 여기에 속한 입력벡터들끼리는 서로 위치적인 유사도를 가진다(=가까운 곳에 있음).

그럼 임의의 입력벡터가 주어졌을 때 2차원상 어떤 격자에 속하는지 어떻게 알 수 있을까요? 위 그림 기준으로 j번째 격자는 원데이터 공간에 존재하는 n차원 벡터 [wj1,wj2,…,wjn]에 대응된다.

다시 말해 2차원상 격자가 위 그림처럼 25개라면 그에 해당하는 n차원 크기의 격자벡터도 25개 있다는 이야기.

임의의 n차원 입력벡터가 들어왔을 때 가장 가까운 격자벡터를 찾습니다. 이것을 Winning node라고 합니다. 이 벡터에 대응되는 2차원상 격자에 해당 입력벡터를 할당하면 이것이 바로 군집화가 되는 것.

같은 격자에 할당된 입력벡터라 하더라도 Winning node와의 거리가 제각기 다를 수 있습니다. 이러한 멀고 가까움 또한 표시를 하게 되면 고차원 공간의 원데이터를 2차원 내지 3차원으로 차원을 축소하는 효과까지 낼 수 있습니다.

SOM의 결과물 예시

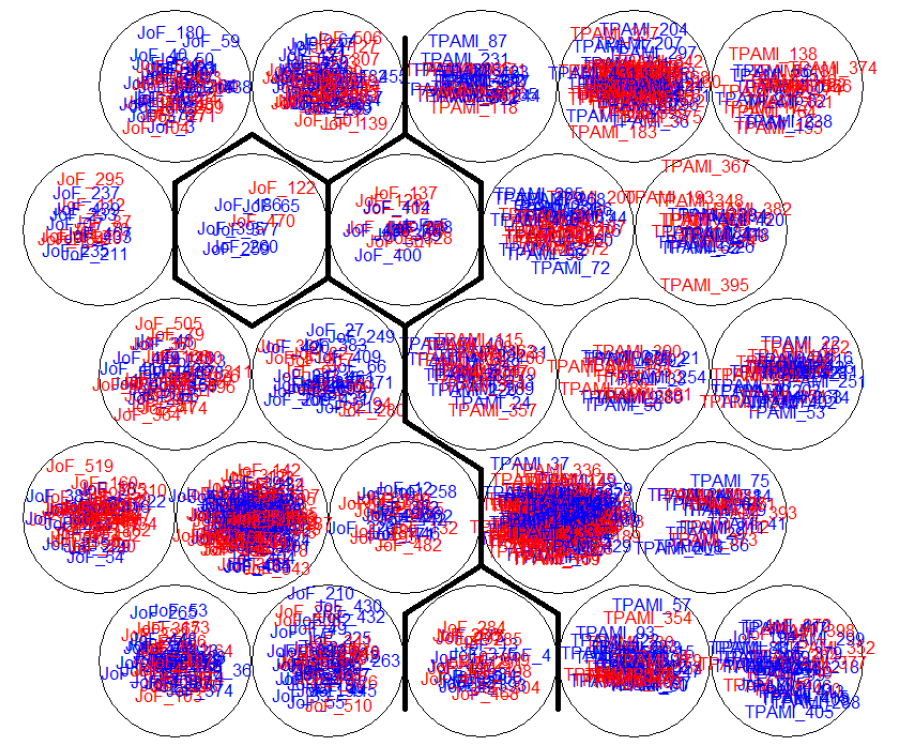
고차원 공간의 원데이터가 25개 격자에 각각 할당(군집화)돼 있고, 동일한 격자에 할당된 입력값끼리도 그 위치가 서로 다르게 임베딩된 것을 확인할 수 있습니다.

K-평균 Clustering

갑자기 Clustering에 대해서 이야기하는 이유는 SOM의 과정에서 Clustering이 제외될 수 없을만큼 중추적인 역할을 하고있기 때문이다.

Clustering이란?

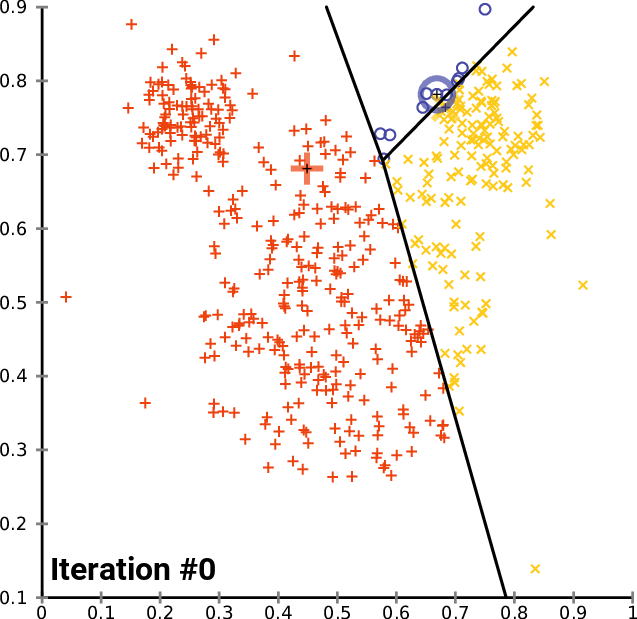
유사한 속성들을 갖는 데이터를 일정한 수의 군집으로 그룹핑하는 비지도 학습입니다.

지금까지 다루었던 머신러닝 모델(선형회귀, 다중선형회귀, 결정트리)는 특정 독립변수에 대한 종속변수(레이블, 정답)이 있는 경우입니다. 하지만 클러스터링의 경우는 정답이 없는 경우에 사용하며 속성별로 데이터를 나누게 됩니다. 때문에 몇개의 군집으로 나누어질지는 분석하는 입장에서 알 수 없다는 특징을 가집니다.

K-평균 군집화(K-Means Clustering)

K-평균 군집화란 대표적인 분할적 군집화 알고리즘으로 사전에 군집의 수(K)를 지정합니다.

각 군집은 하나의 중심점 (centroid, center)이 존재하고 각 데이터들을 가장 가까운 중심점에 해당하는 군집에 할당하는 방식입니다.

K-평균 군집화 알고리즘은 다음과 같습니다.

1.구하고자 하는 군집의 수(K) 설정
2.초기 데이터의 분포 상태에서 K개의 중심점을 임의로 지정
3.각 데이터들로부터 K개의 각 중심점 까지의 거리를 계산
4.각 데이터들을 가장 가까운 중심점이 속한 군집에 할당
5.K개의 중심점을 다시 계산하여 갱신 ( 중심점은 각 군집의 데이터들의 평균값)
6.중심점이 더 이상 변하지 않을 때까지 3, 4, 5 과정을 반복

SOM 학습

그렇다면 SOM은 어떻게 학습을 하는 것일까요? 직관적으로 이해해보기 위해 아래 그림을 먼저 살펴보겠습니다. 시각화를 위해 원데이터의 차원수와 격자의 차원수는 모두 2차원으로 두었습니다. 하지만 이는 이해를 돕기 위함일 뿐, 검정색 점이 흩뿌려진 원데이터 공간은 고차원이라고 생각하셔야 합니다.

위 그림에서 연두색 25개 점은 고차원의 원데이터공간에 대응되는 격자벡터입니다. 처음엔 그 위치를 랜덤으로 초기화합니다. 이후 학습데이터 x(검정색 점)를 하나씩 추가해가며 격자벡터의 위치를 x의 위치와 비슷해지도록 업데이트합니다(instance-based learning).

다만 여기서 주의해야할 것은 격자벡터의 업데이트 폭이 모두 같지는 않다는 점입니다. 현재 주어진 x와 그 위치가 가장 가까운 Winning node가 제일 많이 업데이트되고요, 이 노드의 주변 격자벡터들은 그보다 조금 덜 업데이트됩니다. 멀리 떨어진 녀석들은 거의 업데이트가 되지 않도록 합니다.

t시점의 j번째 격자벡터를 업데이트하는 과정을 수식으로 나타내면 아래와 같습니다.

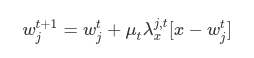
여기에서 $μ$는 일종의 learning rate로 반복 횟수가 커지면 학습 속도를 줄이는 역할을 합니다. $λ$는 Winning node는 가장 크게, 학습데이터와 멀리 떨어진 격자벡터는 작게 업데이트하도록 합니다(가우시안 분포 활용). 마지막으로 괄호 안의 뺄셈으로 된 부분은 학습데이터 $x$와 격자벡터 간 차이를 의미하는데, 벡터의 덧/뺄셈 결과 역시 벡터이므로 격자벡터가 업데이트되는 방향을 결정해줍니다.