출처:
지미뉴트론 개발일기

텐서, 행렬의 곱셈

PyTorch tensors can leverage GPU acceleration, while NumPy arrays are CPU-bound.

• 일반적으로 행렬(matrix)이란 2차원 구조(행과 열)를 갖는 것을 가리키고, 행렬을 일반화한 것(즉, 3차원, 4차원 등으로 확장한 것)을 텐서(Tensor)라 지칭
  • Numpy에서는 텐서 대신에 배열(Array)이라 함

• 용어 구분하기
  • 내적(dot product)
    • 두 벡터 a와 b의 내적 a·b: 스칼라를 생성함
    • A · B = |A| |B| cosθ로 표현
    • 두 벡터 사이의 각도 θ에 따라 결정되며, 같은 방향 성분을 곱하는 것으로 해석됨
  • 외적(cross product)
    • 두 벡터 a와 b의 외적 a×b: 벡터를 생성함
    • a와 b가 3차원 벡터일 때만 정의
    • 외적의 결과는 a와 b 모두에 수직인 벡터로, 오른손 법칙을 사용하여 방향을 결정할 수 있음
  • 행렬곱(matrix multiplication): 두 행렬을 곱하는 것
    • Matrix multiplication follows the rules of linear algebra and requires compatible dimensions for the operation.
  • 텐서곱(tensor product): 두 텐서를 곱하는 것

• 공식 문서 설명 살펴보기
  • numpy.dot(a, b, out=None): Dot product of two arrays.
    • numpy.dot은 두 배열의 내적곱(dot product)
  • numpy.matmul(a, b, out=None): Matrix product of two arrays.
    • numpy.matmul은 두 배열의 행렬곱(matrix product)

• 더 알아보기
  • Numpy에서 제공하는 두 함수 dot과 matmul은 2차원 행렬의 곱셈에서는 서로 같은 기능을 수행한다. 하지만 고차원 배열 또는 텐서의 곱셈에서는 그 용법이 전혀 다르다.
  • Pytorch에서도 dot 함수와 matmul 함수를 지원하고, Numpy처럼 두 함수 간 차이가 있음

numpy와 pytorch 비교

• numpy의 곱 연산
  • * 연산자
    • 원소별(element-wise) 연산
    • 스칼라 곱
    • 브로드캐스팅 지원
  • numpy.dot 함수
    • 두 행렬 간의 내적(dot product)
    • 앞의 행렬의 마지막 축과 뒤의 행렬의 두 번째 축 간의 내적 수행
  • @ 연산자
    • 행렬이라는 2차원 공간에서는 내적 dot과 같은 역할
    • 3차원부터는 텐서곱(외적)이라 다른 결과
    • 마지막 축에 대해서만 행렬 곱셈
    • numpy.matmul과 동일
    • pytorch의 matmul, @와 동일
• pytorch의 곱 연산
  • * 연산자
    • In PyTorch, the * operator is used for element-wise multiplication (also known as the Hadamard product) between two tensors.
    • It is important to distinguish this from matrix multiplication, which is performed using the @ operator or functions like torch.matmul() or torch.mm().
  • torch.dot 함수
    • Unlike NumPy’s dot, torch.dot intentionally only supports computing the dot product of two 1D tensors with the same number of elements.
  • torch.mul(t1,t2) 함수 / t1.mul(t2) 메서드
    • 원소별(element-wise) 곱셈
    • 브로드캐스팅 지원
  • torch.matmul 함수
    • 행렬 곱셈
    • 3차원부터는 텐서곱(외적)
    • @와 동일

numpy - * vs pytorch - mul

# NumPy에서의 *
A_numpy = np.array([[1, 2, 3]])
B_numpy = np.array([[2], [2]])

result_numpy = A_numpy * B_numpy

print(A_numpy.shape, B_numpy.shape)

# pytorch에서의 mul
A_torch = torch.tensor([[1, 2, 3]])
B_torch = torch.tensor([[2], [2]]) 

result_torch = torch.mul(A_torch, B_torch)


print("NumPy * result:\n", result_numpy)
print("PyTorch mul result:\n", result_torch)

(1, 3) (2, 1)

NumPy * result:
 [[2 4 6]
 [2 4 6]]

PyTorch mul result:
 tensor([[2, 4, 6],
        [2, 4, 6]])

numpy - dot, @(=matmul)

# 3차원 배열 생성
A = np.random.rand(2, 3, 4)
B = np.random.rand(2, 4, 5)

# np.dot 수행
result_dot = np.dot(A, B)

# @ 연산자 수행
result_at = A @ B

print("Shape of A:", A.shape)
print("Shape of B:", B.shape)

# 앞의 행렬의 마지막 축과 뒤의 행렬의 두 번째 축간의 내적 수행
# 2차원 행렬인 경우 행렬내적으로 같은 결과가 나오겠지만
# 3차원 텐서부터 'dot' 결과값 다름
print("Shape of Result (dot):", result_dot.shape)
print("Shape of Result (@):", result_at.shape)

Shape of A: (2, 3, 4)
Shape of B: (2, 4, 5)
Shape of Result (dot): (2, 3, 2, 5)
Shape of Result (@): (2, 3, 5)

• 2차원 행렬곱에서는 np.dot 과 np.matmul(=@) 연산이 행렬내적으로 동일하나 3차원 이상의 텐서곱 연산에서는 np.matmul(=@) 외적으로 연산함.

pytorch - matmul, @

# 3차원 텐서 생성
A = torch.rand(2, 3, 4)
B = torch.rand(2, 4, 5)

# torch.matmul 수행
result_matmul = torch.matmul(A, B)

# @ 연산자 수행
result_at = A @ B

print("Shape of A:", A.shape)
print("Shape of B:", B.shape)
print("Shape of Result (matmul):", result_matmul.shape)
print("Shape of Result (@):", result_at.shape)

Shape of A: torch.Size([2, 3, 4])
Shape of B: torch.Size([2, 4, 5])
Shape of Result (matmul): torch.Size([2, 3, 5])
Shape of Result (@): torch.Size([2, 3, 5])

• 2차원 torch.matmul, @, np.matmul(=@)는 2차원 행렬연산에서는 np.dot과 동일하지만 3차원 이상 텐서곱에서는 외적으로 np.dot과 다름

np.matmul과 np.dot이 같은 결과를 나타내는 경우

1. 1차원 * 1차원 (내적 연산)

import numpy as np

# 1차원 * 1차원
a = np.array([1, 3, 5])
b = np.array([4, 2, 0])

np.dot(a, b) # 10
a @ b # 혹은 np.matmul(a, b) # 10

2. 2차원 * 2차원 (2차원 행렬곱)

# 2차원 * 2차원
a = np.array([[1, 3], [2, 4]])
b = np.array([[1, 0], [2, 1]])

np.dot(a, b)
'''
array([[ 7,  3],
       [10,  4]])'''

a @ b # 혹은 np.matmul(a, b)
'''
array([[ 7,  3],
       [10,  4]])'''

3. 2차원 1차원 or 1차원 2차원 (행렬 * 벡터곱 연산)

# 2차원 * 1차원
a = np.array([[1, 3], [2, 4]])
b = np.array([2, 1])

np.dot(a, b) # array([5, 8])
a @ b # array([5, 8])

# 1차원 * 2차원
np.dot(b, a) # array([ 4, 10])
b @ a # array([ 4, 10])

np.matmul과 np.dot이 다른 경우

1. 배열과 스칼라의 곱
   • np.dot 함수는 np.multiply에서 제공하는 스칼라와 배열의 곱을 지원하지만, np.matmul 함수는 스칼라와 배열의 곱에서 오류가 발생합니다.

# 배열 * 스칼라
a = np.array([1, 3, 5])
b = 2

np.dot(a, b) # array([ 2,  6, 10])
a @ b # ValueError: matmul: Input operand 1 does not have enough dimensions (has 0, gufunc core with signature (n?,k),(k,m?)->(n?,m?) requires 1)

2. 3차원 이상 다차원 배열곱
   • 3차원 이상의 다차원 배열에서 연산을 수행하는 방식이 다릅니다.
     • np.dot(a, b)는 a의 마지막 axis와 b의 마지막에서 두번째 axis끼리 곱한 결과를 반영
     • np.matmul(a, b)는 a의 마지막 두 axis 차원이 (n, k), b의 마지막 두 axis 차원이 (k, m)일 때, 이 사이에서만 곱하여 (n, m) 차원이 되도록 반영

# 2차원 * 3차원
a = np.array([[1, 3], [2, 4]])
b = np.array([[[1, 1], [0, 1]], [[5, 0], [0, 0]]])

np.dot(a, b)
'''
array([[[ 1,  4],
        [ 5,  0]],

       [[ 2,  6],
        [10,  0]]])'''

a @ b
'''
array([[[ 1,  4],
        [ 2,  6]],

       [[ 5,  0],
        [10,  0]]])'''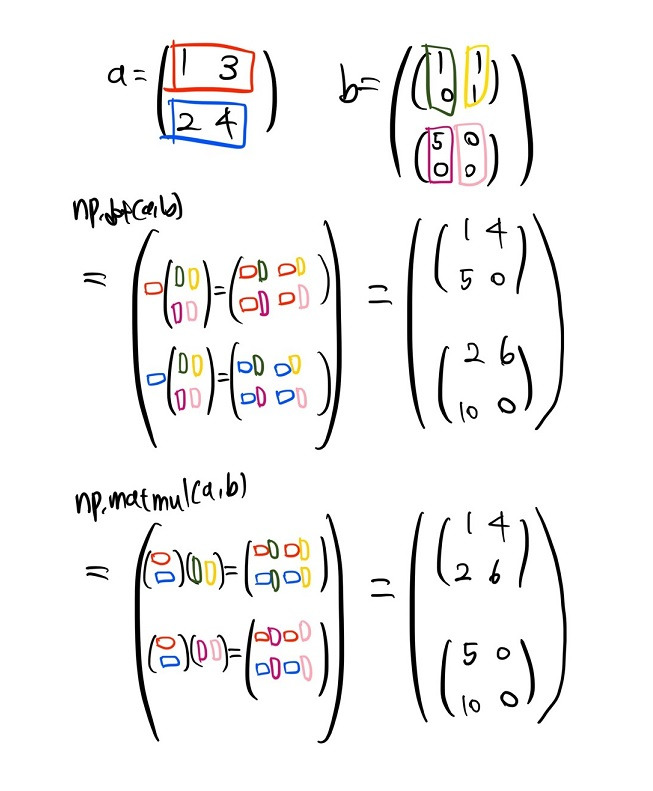

• np.dot에서는 a의 마지막 axis 방향인 행 방향을 각각 가져와 b의 마지막에서 두번째 axis 방향인 열 방향을 각각 가져온 결과를 곱함
• np.matmul에서는 a 행렬의 마지막 axis 두개는 a 행렬 전체이기에, a 행렬 전체를 가져와 b의 마지막 axis 두 개에 해당하는 각각의 행렬 부분을 곱한 결과를 반환

a = np.ones([5, 7, 4, 3])
b = np.ones([5, 7, 3, 6])

np.dot(a, b).shape # (5, 7, 4, 5, 7, 6)
np.matmul(a, b).shape # (5, 7, 4, 6)

• np.dot에서는 a의 (5, 7, 4, 3)과 b의 (5, 7, 3, 6)에서 a의 마지막 axis와 b의 마지막에서 두 번째 axis끼리 곱하여 모든 값이 3인 (5, 7, 4, 5, 7, 6) 차원의 배열 반환
  • a의 마지막 axis와 b의 마지막에서 두 번째 axis의 숫자가 다르면 오류가 발생
• np.matmul에서는 a의 (5, 7, 4, 3)과 b의 (5, 7, 3, 6) 부분에서 마지막 두 axis씩을 가져와 곱하면 (4, 3) (3, 6) -> (4, 6)이 되어(행렬곱 : (n, k) (k, m) -> (n, m)) 최종 결과는 모든 값이 3인 (5, 7, 4, 6) 차원이 됨
  • 두 배열 사이의 k 부분 숫자가 다르거나 앞 부분 숫자(예시의 (5,7))가 다르면 오류 발생

Function	Condition (3-D)	Formula (3-D)
np.dot	A.shape # (a1, a2, a3) B.shape # (b1, b2, b3) --> a3==b2 >>> C = np.dot(A,B) >>> C.shape (a1, a2, b1, b3)	C[i,j,k,m] = np.sum(A[i,j,:] * B[k,:,m])
np.matmul	A.shape # (a1, a2, a3) B.shape # (b1, b2, b3) --> (a1==b1) and (a3==b2) >>> C = np.matmul(A,B) >>> C.shape (a1, a2, b3)	C[i,j,k] = np.sum(A[i,j,:] * B[i,:,k])

np.dot() 사용법 더 알아보기