[인공지능사관학교: 자연어분석A반] 딥러닝 (6)

Suhyeon Lee·2025년 7월 18일
인공지능사관학교

코딩테스트 연습

알고리즘

SQL



지난 시간 복습

  • 당뇨병 데이터 분석
    • sklearn 번치 객체 → 데이터프레임으로 옮기기
    • 10개의 입력 특성과 1개의 정답 데이터
    • 정답 데이터: 연속형 → 회귀
  • 히스토그램
    • 수치형 데이터 → bins라는 묶음으로 나눠 정규분포가 잘 형성되어 있는지 데이터 형태 확인
    • 종 모양이 나오면 정규분포를 따름
    • 정규분포를 이루지 않는 데이터 예시: 봉우리가 한쪽으로 치우쳐 있음(a long tail distribution)
  • torch 형태(tensor)로 데이터 변환
    • sklearn은 array 형태로 데이터 제공하기 떄문
    • PyTorch의 브로드캐스팅 규칙 + 연산 일치 조건 때문에 차원 확장 필요!
      • 정답 데이터 2차원으로 변경 (unsqueeze)
      • 또는 X와 y를 하나의 데이터프레임으로 받은 뒤 분리할 때 슬라이싱으로 나누면 차원 일치함
  • 신경망 모델 설계를 위한 라이브러리
    • import torch.nn as nn
  • 선형회귀모델
    • nn.Linear
  • 최적화함수
    • torch.optim as optim
      • 모델 파라미터 값 넣어줘야 함: model.parameters()를 최적화 함수에 넘겨 주기(optim.SGD(model.parameters(), lr=0.00001)
  • 손실 함수
    • import torch.nn.functional as F
    • F.mse_loss(y_pred, y_
  • 반복문
    • tqdm 반복문에 넣기
    • 최적화 함수 optimizer.zero_grad로 초기화
      • 이전에 반복 계산한 결과 초기화
    • 가중치 업데이트: optimizer.step()

실습: 딥러닝 회귀 모델

학습 결과 확인

# 결과를 시각화할 때 텐서 연산의 결과를 초기화 후 넘파이 배열로 변경하여 시각화 하는 것이 안전
# 텐서를 끊고(.detach()) 넘파이로 바꿈(.numpy())

# 예측값(y_pred) 결과의 텐서를 해제하고 넘파이로 변환
np_pred = y_pred.detach().numpy()

# 시각화 → 산점도 그래프
plt.scatter(x=np_pred, y=y)
plt.show()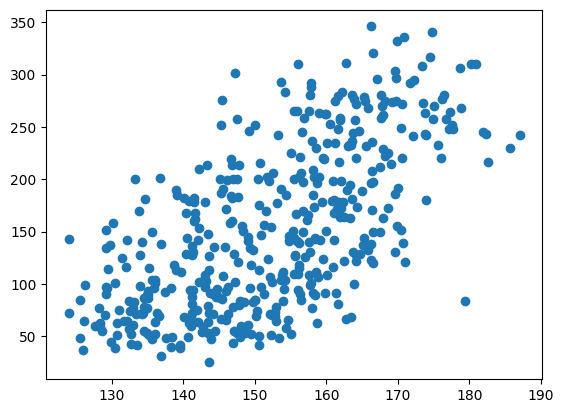

  • 대각선 방향으로 좁게 분포되어 있어야 좋은 모델!
    • 위의 예시는 되게 오차가 큰 편 → 선형 회귀 모델 한 개만 사용했기 때문

DNN

학습 목표

  • 심층심경망(DNN)을 설계하는 방법에 대해 알고 실습할 수 있다.

오차 역전파(Back Propagation)

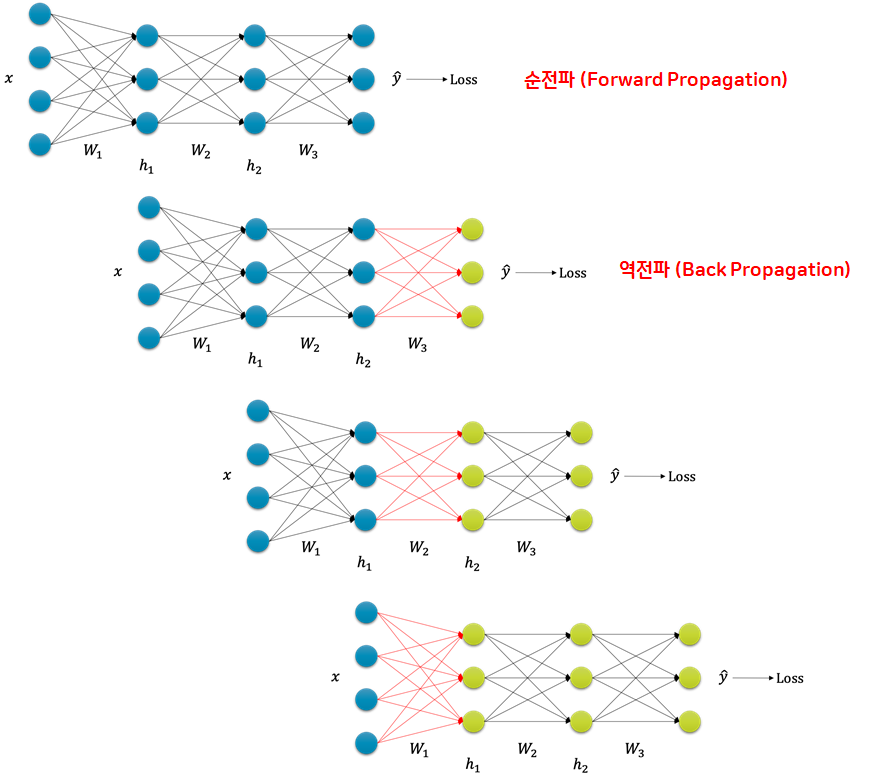
  • 오차를 출력층에서 입력층으로 전파시키면서 최적의 파라미터를 찾아가는 과정
    1. 순전파(Forward Propagation) 수행: 입력 데이터를 입력층에서 출력층까지 전파시키면서 출력값을 찾아가는 과정 → '예측', '추론' 과정
    2. 순전파로 오차를 계산
    3. 오차를 다시 출력층에서 입력층으로 전파시키면서 파라미터를 업데이트 → '학습' 과정

기울기 소실(Vanishing Gradient)

  • 심층신경망에서 입력층으로 갈수록 가중치 파라미터가 업데이트되지 않는 문제 (제대로 된 학습이 되지 않는 문제)
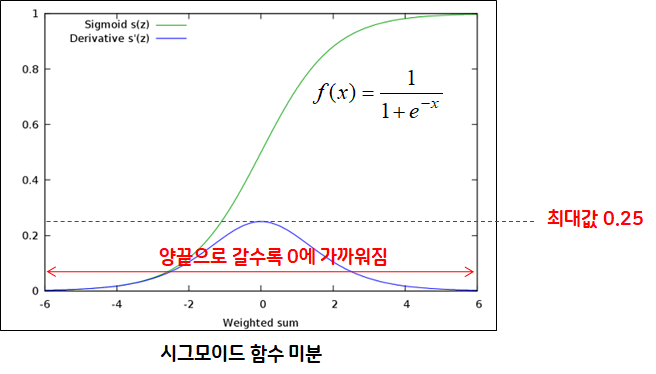
  • 주로 깊은 층의 활성화 함수로 시그모이드(sigmoid) 함수를 사용했을 때 발생
    • 오차역전파 시 층마다 존재하는 활성화 함수(sigmoid) 미분하여 곱해지면서 기울기 소실
      • sigmoid 함수를 미분하면 최댓값이 0.25가 되면서 오차가 손실됨
  • ReLU 활성화 함수를 하용하여 가울기 소실 문제를 해결
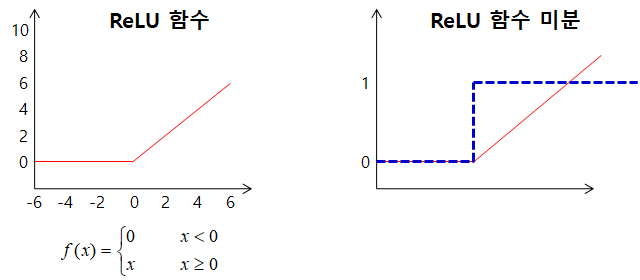
    • 미분하면 음수 구간은 0으로, 양수 구간은 1로 출력하여 역전파 시 기울기에 영향을 주지 않는다.
    • 음수 구간의 경우 미분값이 0이 되기 때문에 기울기 소실이 발생하기는 함 → 다양한 형태의 ReLU를 사용하기도 한다.
      • 예: Leaky-ReLU

추가: Sigmoid 함수 미분하기

  • 딥러닝에서 활성화 함수를 사용할 때 시그모이드(Sigmoid) 함수를 많이 사용 → 역전파를 보내기 위해서는 편미분값을 보내야 함
    • 시그모이드 함수를 수식적으로 미분해보자
      • 시그모이드의 미분은 다시 시그모이드의 함수로 구할 수 있는 꼴이 나옴
f(x)=11+e−xf(x) = \frac{1}{1+e^{-x}}
dfdt=−1t2⋅dtdx(t=1+e−x)\frac{df}{dt} = -\frac{1}{t^2}\cdot \frac{dt}{dx}\quad(t=1+e^{-x})
⇒1(1+e−x)2⋅e−x\Rightarrow\frac{1}{(1+e^{-x})^2}\cdot e^{-x}
⇒1+e−x−1(1+e−x)(1+e−x)\Rightarrow\frac{1+e^{-x}-1}{(1+e^{-x})(1+e^{-x})}
⇒(1+e−x)(1+e−x)2−1(1+e−x)2\Rightarrow\frac{(1+e^{-x})}{(1+e^{-x})^2}-\frac{1}{(1+e^{-x})^2}
⇒11+e−x⋅(1−11+e−x)\Rightarrow\frac{1}{1+e^{-x}}\cdot(1-\frac{1}{1+e^{-x}})
⇒f(x)⋅(1−f(x))\Rightarrow f(x)\cdot(1-f(x))
  • x=0일 때 시그모이드 함수의 기울기 구하기
f′(x)=f(x)⋅(1−f(x))f'(x) = f(x)\cdot(1-f(x))
f′(0)=f(0)⋅(1−f(0))=12⋅(1−12)=14f'(0) = f(0)\cdot(1-f(0)) = \frac{1}{2}\cdot(1-\frac{1}{2}) = \frac{1}{4}
  • 시그모이드 함수의 기울기는 0일 때 최댓값을 가지며 좌우로 갈수록 기울기는 감소
    • input 값이 커지거나 작아질수록 기울기가 줄어듦을 의미 → vanishing gradient

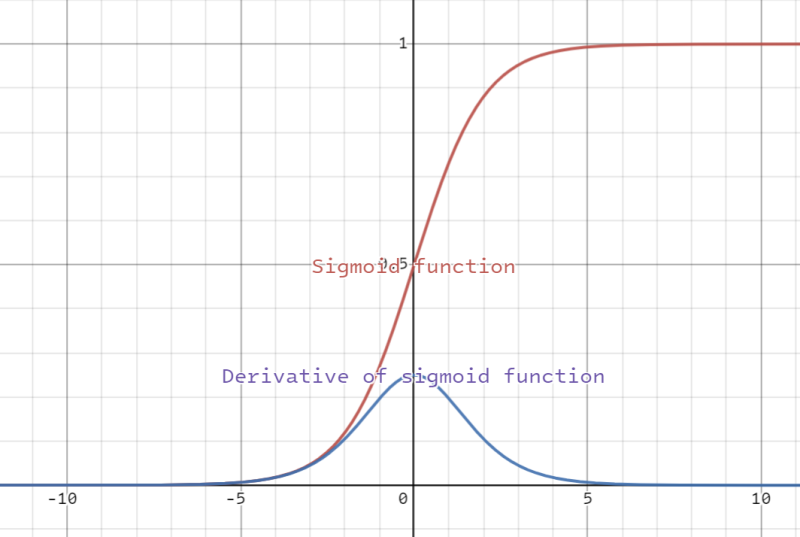
  • vanishing gradient problem
    • 역전파 알고리즘을 수행할 때 편미분 값을 이전 노드에 전달하게 되는데, 만약 input 값이 너무 커 기울기가 0에 가깝다면 이전 노드에 전파를 전달하더라도 무의미
    • 따라서 활성화 함수를 시그모이드가 아닌 Tanh(x)나 ReLU(x) 등을 사용하기도 함

실습: 캘리포니아 집값 예측

  • 심층신경망 구현 (회귀)
# 라이브러리 불러오기
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from tqdm import tqdm

from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
# 데이터 불러오기
from sklearn.datasets import fetch_california_housing

# 데이터프레임에 담기
data=fetch_california_housing()
h_data=pd.DataFrame(data.data, columns=data.feature_names)
h_data["price"]=data.target
h_data.shape
(20640, 9)

🏠 California Housing Dataset 컬럼 설명

컬럼명설명
MedInc지역의 중간 소득 (단위: 10,000달러)
HouseAge주택 연식 (해당 지역 내 평균 주택 연수)
AveRooms가구당 평균 방 수
AveBedrms가구당 평균 침실 수
Population지역 내 인구 수
AveOccup가구당 평균 거주 인원
Latitude위도
Longitude경도
Price주택의 중간 가격 (단위: 100,000달러)
→ MedHouseVal 컬럼이 Price 역할을 함

데이터 스케일링

  • Standard Scaler: 데이터 평균 0으로, 분산이 1로 되도록 범위를 정규화
  • 대부분 scaler 기본값으로 standard scaler를 사용
    • 데이터 분포가 정규분포 형태로 생겼으면 대부분 standard scaler 씀
  • 히스토그램 확인
h_data.hist(figsize=(10,10))
plt.tight_layout()
plt.show()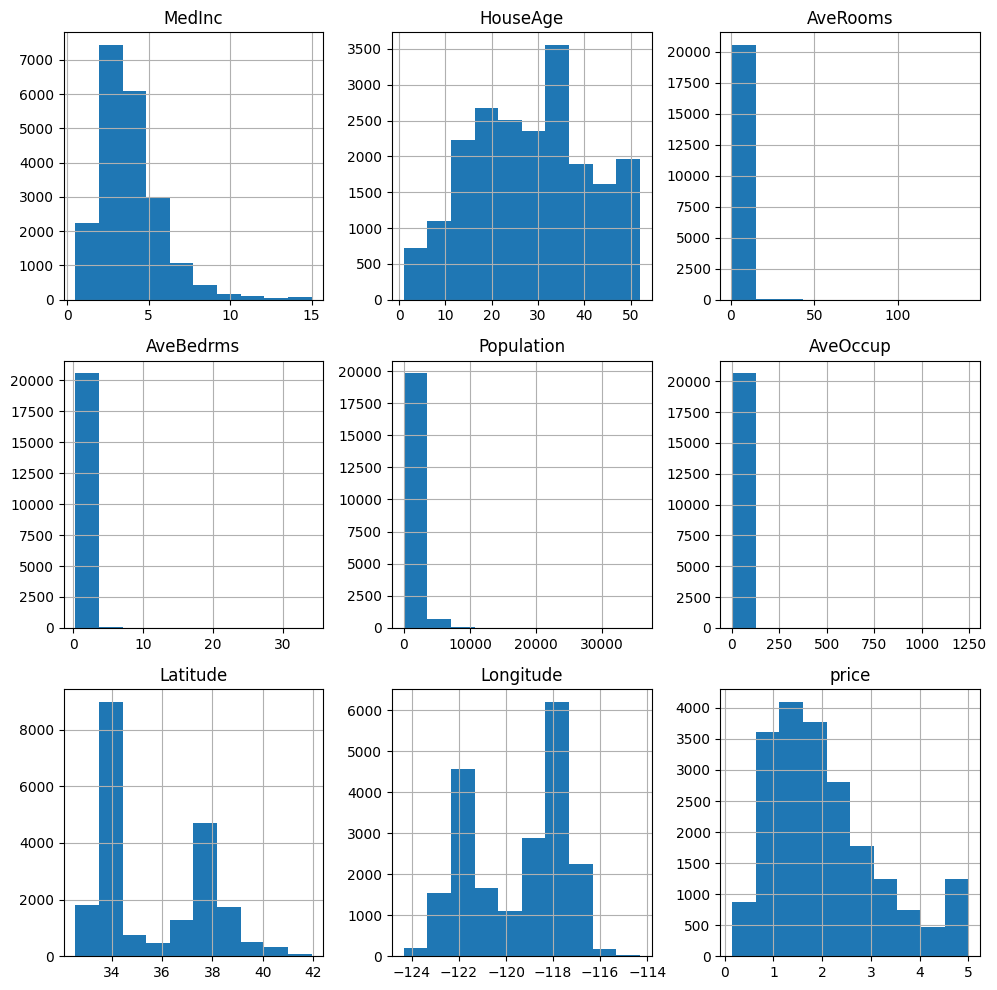

# 객체 생성
st_scaler = StandardScaler()

# 입력특성 데이터 스케일링 → 정답 데이터 제외하고!
h_data.values[:,:-1] = st_scaler.fit_transform(h_data.values[:,:-1])

# 문제와 정답으로 분리
# numpy 형태의 데이터를 tensor 형태로 변경
t_data = torch.from_numpy(h_data.values).float()

# 문제, 정답 분리
X = t_data[:,:-1]
y = t_data[:,-1:] # 정답 데이터를 2차원으로 출력해 주기 위해 (unsqeeze 안 하려고)
print(X.shape, y.shape)
torch.Size([20640, 8]) torch.Size([20640, 1])

심층신경망 설계

  • PyTorch에서는 딥러닝 모델을 class 형태로 설계하는 것이 일반적 → 클래스로 만들어서 사용 == 클래스로 묶어서 한번에 실행
  • cf. tensorflow: 함수를 불러 와 단순 나열
  • 단순한 함수를 불러와 설계하는 문법 사용 형태가 아닌 구조적인 설계를 하기 위해서 & 재사용성, 유연성을 위한 설계법이기 때문

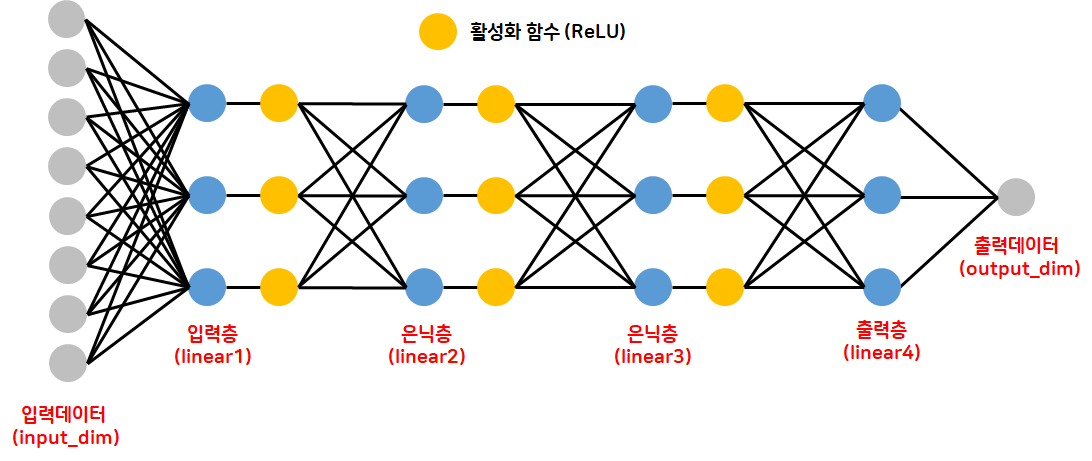
# nn.Module: PyTorch에서 제공하는 기본 모델 클래스 → 상속하여 새 모델 정의
# 상속: 기본 뼈대는 "부모"로 삼고 새로운 클래스를 정의하여 다양한 기능을 만들어 사용할 수 있음

class MyModel(nn.Module): # PyTorch에서 제공하는 기본 모듈 클래스를 상속받겠다는 뜻

    # 모델의 구조(레이어)를 정의하는 함수를 정의
    def __init__(self, input_dim, out_dim): # input_dim, out_dim: 입력 특성의 수, 출력 수를 외부에서 받기
        super().__init__() # 부모 클래스 생성자 호출
        self.input_dim = input_dim # 외부에서 전달받은 argument를 내부에서 사용하기 위해 self로 넣어 주어야 함
        self.out_dim = out_dim        

        # 입력층 → 모델의 입력 layer를 정의
        self.linear1 = nn.Linear(self.input_dim, 3)
        # 중간층(은닉층)
        self.linear2 = nn.Linear(3,3) # 3의 퍼셉트론을 한 개의 층에서 사용하겠다는 뜻
        self.linear3 = nn.Linear(3,3) # 3의 퍼셉트론을 한 개의 층에서 사용하겠다는 뜻
        # 출력층
        self.linear4 = nn.Linear(3, self.out_dim)
        # 활성화함수
        self.act = nn.ReLU()
    
    # 데이터를 입력 받아 연산을 진행하는 함수를 정의
    def forward(self, X):
        h = self.act(self.linear1(X))
        h = self.act(self.linear2(h))
        h = self.act(self.linear3(h))
        y = self.linear4(h) # 회귀 문제 → 출력층 활성화 함수: 항등함수 → 따로 입력할 필요 없음
        return y

# 모델 생성
# MyModel(입력, 출력)
model1 = MyModel(X.size(-1), y.size(-1))

print(model1)
MyModel(
  (linear1): Linear(in_features=8, out_features=3, bias=True)
  (linear2): Linear(in_features=3, out_features=3, bias=True)
  (linear3): Linear(in_features=3, out_features=3, bias=True)
  (linear4): Linear(in_features=3, out_features=1, bias=True)
  (act): ReLU()
)

학습 코드 구현

  • 직접 학습 루프(for 문) 짜는 것이 기본 방식 → 유연성, 직접제어성
# 학습 횟수 및 출력 횟수, 학습률 지정
n_epochs = 4000
print_interval = 200
learning_rate = 0.001

# 최적화 함수 정의
optimizer = optim.Adam(model1.parameters(), lr=learning_rate)

# 학습 반복문 작성
for i in tqdm(range(n_epochs)):
    # 예측 결과
    y_pred = model1(X)
    # 손실 함수를 통한 loss
    loss = F.mse_loss(y_pred, y)
    # 최적화 함수 초기화
    optimizer.zero_grad()
    # 오차역전파
    loss.backward()
    # 결과 담기
    optimizer.step()
    # 결과 출력
    if (i+1)%print_interval==0:
        print(f"epoch: {i+1}, loss: {loss:.4e}")

반복문에서 .forward()를 직접 호출하지 않았는데 왜 학습이 되나요? 자동 실행된 건가요?
네, 맞아요! 반복문 안에서 명시적으로 .forward()를 호출하지 않아도 y_pred=model1(X)를 실행하면 내부적으로 forward()를 자동 실행합니다.
이는 해당 모델 객체가 PyTorch에서 nn.Module을 상속 받아 __call__ 메서드가 재정의되어 있기 때문입니다.
model1(X)는 사실 model1.__call__(X)이고 이 __call__ 메서드 안에서 내부적으로 forward(X)를 호출하도록 되어 있습니다.

  • 요약:
    • 반복문에서 model1(X) 한 줄이면 자동으로 forward(X)가 실행되는 것과 같습니다.
    • 그래서 .forward(X)를 직접 호출하지 않아도 모델이 작동해요.
  • torch.nn.Module(*args, **kwargs) 클래스
    • Base class for all neural network modules.
    • Your models should also subclass this class.
    • forward(*input)
      • Define the computation performed at every call.
      • Should be overridden by all subclasses.

모델 설계 및 학습

  • nn.Sequential()을 사용하여 모델 구현
    • 작성이 훨씬 간편함
    • 직접 학습 코드 짜는 것보다는 유연성이 떨어지는 편
model2 = nn.Sequential(
    nn.Linear(X.size(-1), 3) # (입력 특성의 수, 퍼셉트론의 수)
    , nn.ReLU() # 활성화 함수
    , nn.Linear(3,3) # (입력 수, 퍼셉트론의 수)
    , nn.ReLU()
    , nn.Linear(3,3)
    , nn.ReLU()
    , nn.Linear(3,y.size(-1))
)

print(model2)

# 학습 횟수 및 출력 횟수, 학습률 지정
n_epochs = 4000
print_interval = 200
learning_rate = 0.001

# 최적화 함수 정의
optimizer = optim.Adam(model2.parameters(), lr=learning_rate)

# 학습 반복문 작성
for i in tqdm(range(n_epochs)):
    # 예측 결과
    y_pred = model2(X)
    # 손실 함수를 통한 loss
    loss = F.mse_loss(y_pred, y)
    # 최적화 함수 초기화
    optimizer.zero_grad()
    # 오차역전파
    loss.backward()
    # 결과 담기
    optimizer.step()
    # 결과 출력
    if (i+1)%print_interval==0:
        print(f"epoch: {i+1}, loss: {loss:.4e}")
Sequential(
  (0): Linear(in_features=8, out_features=3, bias=True)
  (1): ReLU()
  (2): Linear(in_features=3, out_features=3, bias=True)
  (3): ReLU()
  (4): Linear(in_features=3, out_features=3, bias=True)
  (5): ReLU()
  (6): Linear(in_features=3, out_features=1, bias=True)
)


딥러닝 활성화 함수 꼭 알아두기!

  • 활성화 함수 역할
    • 선형 모델이 연산한 결과에 추가 연산
      • 선형 연산만 계속 반복하면 아무리 층을 깊게 쌓아도 결국은 하나의 선형 모델과 동일한 결과
      • 활성화 함수가 없으면 층을 깊게 쌓는 것이 의미가 없음
    • 복잡한 패턴의 데이터 학습을 위하여 비선형 활성화 함수를 사용
      • 복잡한 연산을 도와주는 역할
  • 중간층, 출력층에서의 활성화 함수 역할이 다름
    • 중간층: 활성화 여부(가중치를 얼마나 적용할 것인지)
    • 출력층: 출력 형태로 변경
      • 회귀: 연속형 데이터를 그대로 연속형 데이터로 출력 → 아무런 조치를 취하지 않아도 됨 → TensorFlow에서는 항등함수로 처리, PyTorch에서는 활성화 함수 미사용
      • 이진분류: 연속형 데이터(-∞ ~ ∞) → 확률 값 1개(0 ~ 1 사이 한 개의 확률 값): sigmoid
      • 다중분류: 연속형 → 확률값 (총합이 1인 class 개수만큼의 확률 값): softmax


하루 돌아보기

👍 잘한 점

  • 오늘 배운 내용 중 이해가 잘 안되는 부분에 대해 스스로 공부
  • 야간자율학습 참여

👎 아쉬웠던 점

  • TensorFlow와 PyTorch가 계속 헷갈림

🔬 개선점

  • 주말 동안 머신 러닝 복습 with 미니프로젝트
profile
Suhyeon Lee
2 B R 0 2 B
이전 포스트

[인공지능사관학교: 자연어분석A반] 학습 내용 보충 - 경사하강법 직접 구현하기

다음 포스트

[인공지능사관학교: 자연어분석A반] 학습 내용 보충 - 클래스(Class)와 __call__ 함수 정리

0개의 댓글