지난 시간 복습

• 오차역전파(Backpropagation)
  • 순전파(Forward propagation) 수행 결과를 다시 출력측에서 입력층으로 전파시키며 파라미터를 업데이트

• 심층신경망 구현: 회귀
  
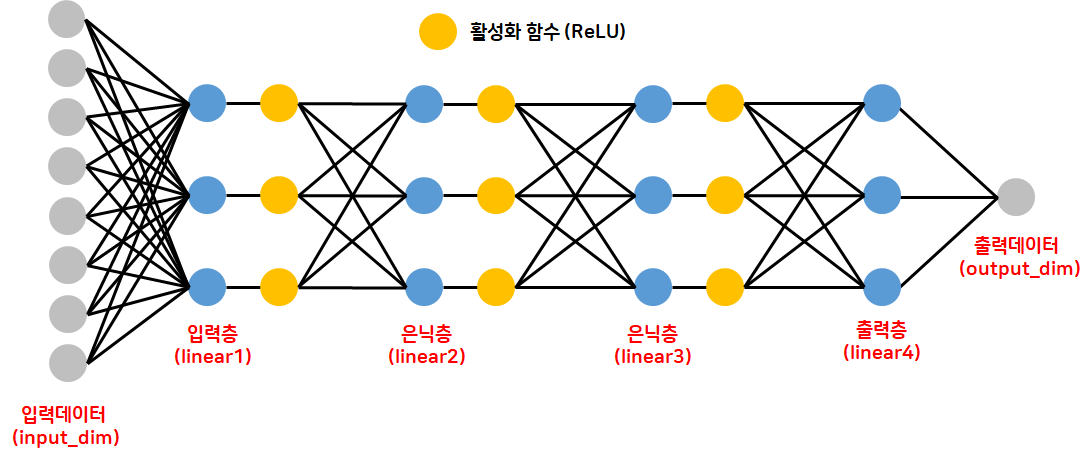
  • 선형 모델은 scaling 해 주는 것이 좋음
    • Standard Scaler: 데이터 평균 0으로 분산이 1로 되도록 범위를 정규화 → 대부분 Scaler 기본 값으로 사용
  • 모델을 class 형태로 사용하는 것이 일반적: 구조적인 설계, 재사용성, 유연성 → class 내부에 들어가야 하는 게 무엇인지 알아두기! (단순한 함수를 불러와 설계하는 문법 사용 형태에서 벗어나자)
    • nn.Module
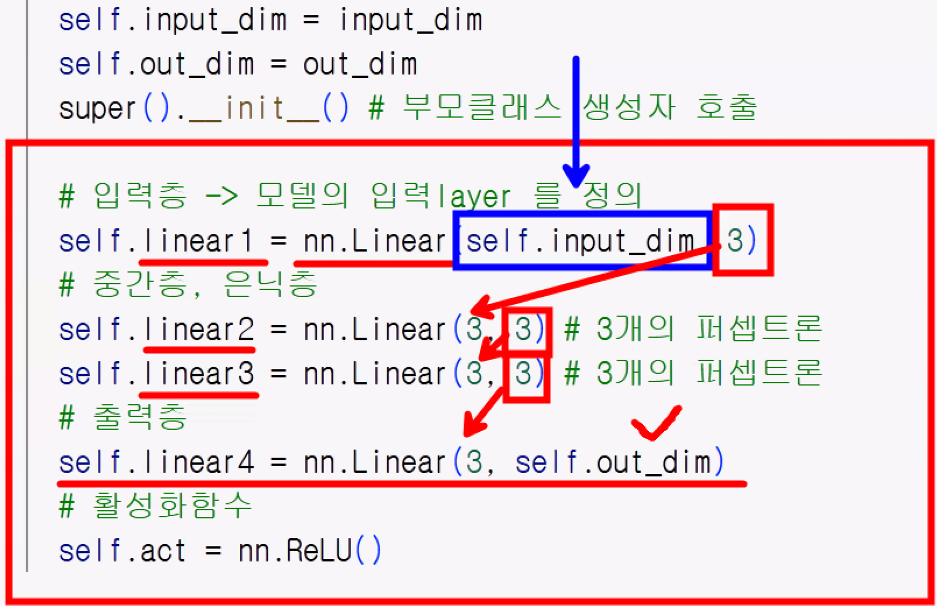
    • def __init__() → 연산(예측)에 사용할 함수들을 정의하는 공간
    • 'self' keyword
    • 입력층, 중간층, 출력층, 활성화 함수
      
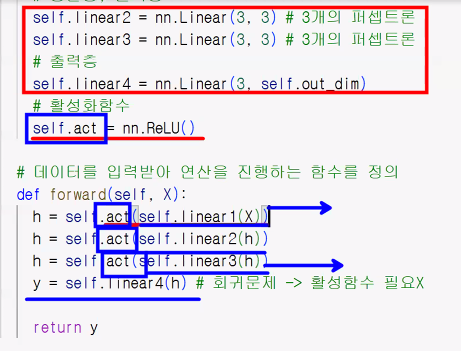
    • forward 함수: 데이터를 입력받아 연산을 진행하는 함수 (정의 필수)
      
    • __init__에서 정의한 내용과 forward 함수 사이의 관계 이해하기
      

• 학습 루프 작성법 꼭 기억하기
  • 직접 학습 루프(for문)을 짜는 것이 기본 방식 → 유연성, 직접제어성

# 학습 횟수 및 출력 횟수, 학습률 지정
n_epochs = 4000
print_interval = 200
learning_rate = 0.001

# 최적화 함수 정의
optimizer = optim.Adam(model1.parameters(), lr=learning_rate)

# 학습 반복문 작성
for i in tqdm(range(n_epochs)):
    # 예측 결과
    y_pred = model1(X)
    # 손실 함수를 통한 loss
    loss = F.mse_loss(y_pred, y)
    # 최적화 함수 초기화
    optimizer.zero_grad()
    # 오차역전파
    loss.backward()
    # 결과 담기
    optimizer.step()
    # 결과 출력
    if (i+1)%print_interval==0:
        print(f"epoch: {i+1}, loss: {loss:.4e}")

오늘 학습할 내용

• validation 데이터 추가해 평가하기
  • 과대적합 방지를 위함
• callback 기능 구현: PyTorch에는 내장 callback 함수가 없어서 직접 조건문으로 만들어야 함
  • best model 저장
  • early stopping

심층신경망: 회귀 - 검증

학습 목표

• PyTorch를 활용하여 심층신경망을 설계할 수 있다.
• 과대적합을 방지하기 위하여 검층 데이터로 분리하여 학습할 수 있다.
• 학습 후 시각화를 통화여 과적합 유무를 확인할 수 있다.

과대적합(Overfitting)

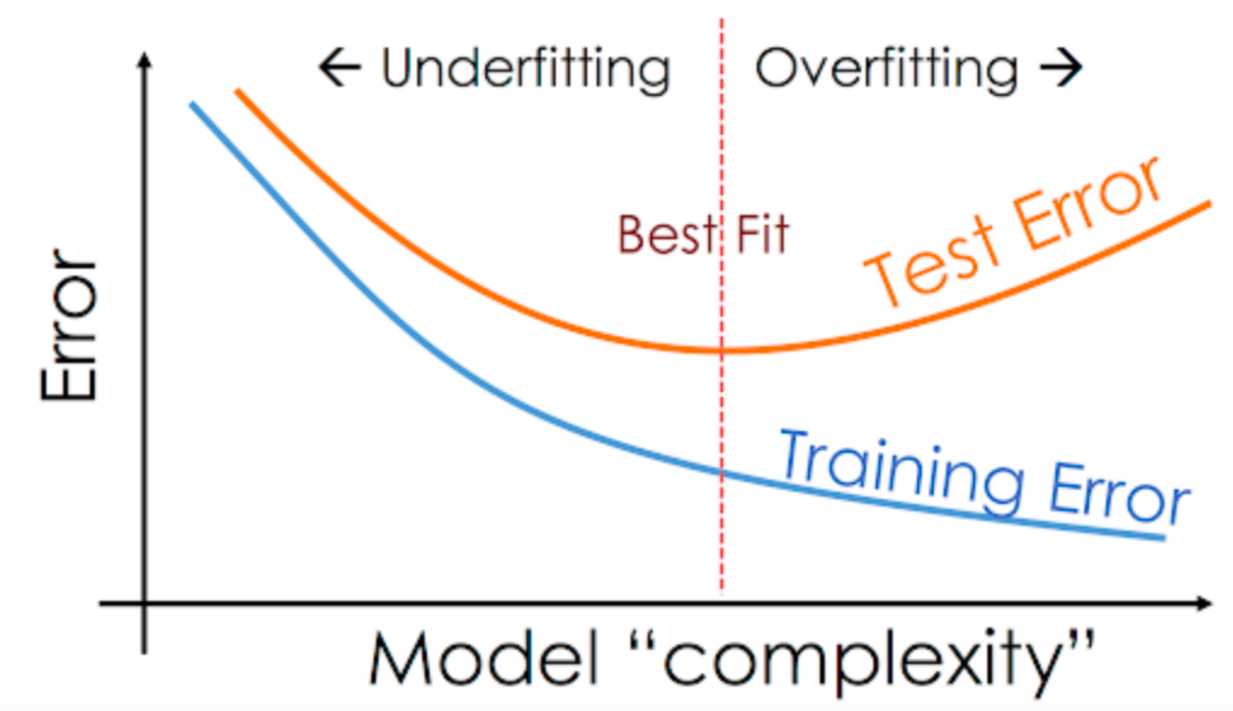
딥러닝에서는 검증과정에서 accuracy보다 loss(Error)를 훨씬 더 많이 사용합니다.

• 과대적합
  • 모델이 학습 데이터(train)에 대해 지나치게 학습하여 새로운 데이터(valid, test)에 대해서는 성능이 떨어지는 문제
• 과소적합(Underfitting)
  • 모델이 학습 데이터에 대해 제대로 학습하지 못하여 성능이 떨어지는 문제
• 일반화
  • 학습 데이터에 대해서도 좋은 성능을 보이며 새로 들어온 데이터에 대해서도 높은 성능을 보이는 것
  • 어떤 데이터 세트에서도 평균적인 성능을 보이는 것
• 모델을 많이 학습시킬수록 "복잡해지기" 때문에 Best Fit에서 저장할 필요가 있음 → 모델 저장 구현 필요

데이터 분리

• 과대적합을 확인하기 위하여 데이터를 분리하여 학습
  • 학습 데이터(train): 학습을 통해 가중치를 업데이트하는 데이터 세트
  • 검증 데이터(valid): 과대적합, 과소적합을 확인할 때 사용
  • 평가 데이터(test): 모델을 최종 평가할 때 사용

Q. 왜 학습과 평가로 과대적합/과소적합을 평가하지 않나요?
A. 하이퍼파라미터를 계속 조절하면서 다시 한번 평가 데이터에 과대적합될 위험이 있기 때문에 평가 데이터는 최종 데이터로 남겨 놓고 학습과 검증 데이터를 통해 하이퍼파라미터 조절 & 과대적합, 과소적합을 확인합니다.

• 학습과 검증 없이 평가 데이터로 하이퍼파라미터 조정을 하면 평가 데이터에 다시 과대적합되는 문제 → 학습 데이터 안에서 다시 학습 데이터와 검증 데이터로 나누고 평가 데이터는 진짜 최종 평가에서만 씀
• 순서
  • 1 단계 : 원본 데이터를 train 데이터와 test 데이터로 분리
  • 2 단계 : train 데이터를 train과 validation으로 분리
  • 3 단계 : train 데이터로 모델을 만들고 validation 데이터로 검증
  • 4 단계 : train 데이터와 validation 데이터를 합쳐서 학습
  • 5 단계 : test 데이터로 평가 (실제로는 신규 데이터를 사용)

검증 데이터로 분리하여 학습 후 과대적합 확인

# 라이브러리 불러오기
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from tqdm import tqdm

from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# 데이터 불러오기
data = fetch_california_housing()

# 데이터를 데이터프레임으로 변경(bunch → DataFrame): 문제와 정답 데이터 합치기
df = pd.DataFrame(data.data, columns=data.feature_names)
df["price"] = data.target

데이터 분리

• 문제, 정답 분리
• 데이터를 랜덤 셔플링하여 훈련, 검증, 평가 데이터로 분리

# 데이터를 텐서 형태로 변환 후 분리
data = torch.from_numpy(df.values).float()

# 문제와 정답으로 분리
X = data[:, :-1]
y = data[:, -1:] # 2차원으로 출력하기 위해 슬라이싱 사용(-1만 쓰면 vector 형태라 크기가 안 맞음)

# train, test, valid 분리 (1. 훈련, 평가 분리 → 2. 훈련 데이터 내에서 훈련, 검증 분리)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=21)
X_train, X_valid, y_train, y_valid = train_test_split(X_train, y_train, test_size=0.25, random_state=21)

print(X_train.shape, X_test.shape, X_valid.shape)
print(y_train.shape, y_test.shape, y_valid.shape)

torch.Size([12384, 8]) torch.Size([4128, 8]) torch.Size([4128, 8])
torch.Size([12384, 1]) torch.Size([4128, 1]) torch.Size([4128, 1])

데이터 스케일링

std_scaler = StandardScaler()

# 스케일링을 진행하려면 numpy 배열 형태여야 함
std_scaler.fit(X_train.numpy())

# train, test, valid 변환
X_train = torch.from_numpy(std_scaler.transform(X_train.numpy())).float()
X_test = torch.from_numpy(std_scaler.transform(X_test.numpy())).float()
X_valid = torch.from_numpy(std_scaler.transform(X_valid.numpy())).float()

학습 모델 설계

• 새로운 개념을 PyTorch로 구현하기
  • 베스트 모델 저장
  • 조기 학습 중단
  • 배치 학습(batch_size)
  • 검증 데이터로 검증
  • 학습 결과 시각화
  • 테스트 데이터 활용 평가

batch_size

• 데이터 중 일부를 샘플링하여 학습
  • 대용량 데이터 세트를 한 번에 처리하면 메모리 문제 발생
    • 공깃밥을 한 번에 바로 다 먹을 수 없음 → 숟가락으로 일정한 양만큼 먹기 == 배치 사이즈 설정
• batch_size: 학습을 위하여 한 번에 신경망에 묶는 '데이터 묶음'
• 데이터를 한 번에 학습시키는 것이 아니라 일정한 크기로 잘라서 조금씩 학습시킨다.
  • 기본 batch_size = 32

• iteration: 데이터를 batch_size로 쪼갠 다음 묶은 단위
  • 예: 100개의 데이터 세트
    • 20개의 batch_size를 사용한다면: iteration은 5개 묶음
• 1 epoch = batch_size*iteration

• 1 epoch의 결과는 iteration을 모두 수행한 '최종 모델 상태'를 의미
• 마지막 iteration에서의 파라미터 상태(w,b) 값을 1 epoch의 결과로 본다
• 1 epoch의 최종 loss는 1 epoch 내 모든 iteration의 평균

# Sequentual() 활용하여 모델 설계 → 간단하게 확인할 때 많이 사용
model = nn.Sequential(
    nn.Linear(X_train.size(-1), 3)
    , nn.ReLU()
    , nn.Linear(3, 3)
    , nn.ReLU()
    , nn.Linear(3, 3)
    , nn.ReLU()
    , nn.Linear(3, y_train.size(-1))
)

n_epochs = 4000
print_interval = 100

# 배치 사이즈 설정 → 한 번의 학습에 사용하는 데이터 수
batch_size = 256

# 최적화 함수
optimizer = optim.Adam(model.parameters()) # lr은 기본값(0.001) 쓸 거라 따로 기재하지 않음

학습 시 모델 저장, 조기 학습 중단 설정

• 모델 저장: 이전 epoch보다 개선된 모델을 저장(loss가 줄어든 모델)
  • 전체 학습 횟수를 모두 진행했을 시 과적합 된 경우 중간 학습 횟수 모델을 사용하기 위함
  • 나중에 다시 불러서 사용하려고
• 조기 학습 중단: 설정된 횟수 내에 오차가 줄어들지 않으면 학습 중단
  • 1000번 학습 → 100번부터 더 이상 오차가 줄지 않으면 모델 성능 개선이 없는 의미 → 학습 의미가 없음(시간낭비) → 시간낭비를 줄이기 위해 중단

# 모델 학습 전 학습 상태 추적을 위한 변수 초기화
train_history, valid_history = [], []

# best 모델 저장할 변수
best_model = None

# 비교를 위한 최소 오차 → 가장 처음 들어온 오차보다 무조건 커야 함 (∴무한대로 설정)
lowest_loss = np.inf

# 학습 중단에 필요한 대기 epoch 수
early_stop = 200

# 학습 중단 기준이 되는 최소 손실값을 갖는 epoch 저장
lowest_epoch = np.inf

학습 과정

• 훈련 데이터를 랜덤으로 섞어가면서 batch_size 만큼의 크기로 자름
  • 매 배치마다 데이터 순서를 랜덤으로 섞기 → 매번 똑같은 배치, 똑같은 순서로 학습하면 모델의 일반화에 도움이 되지 않음(과대적합 위험성)
• epoch 마다 batch_size를 가져와서 학습
• 검증 데이터의 손실값 계산하여 저장
• 현재 epoch의 검증 손실값이 현재의 최소 손실보다 작다면? 모델 저장!
• 지정한 일정 횟수 이상 검증 손실값이 최소 손실보다 계속 크다면? 모델 학습 중단!

# 학습 반복 시작!

# 데이터를 복사하는 라이브러리
from copy import deepcopy
# 저장할 모델을 복사하여 best_model에 저장할 때 사용

for i in tqdm(range(n_epochs)):
    indices = torch.randperm(X_train.size(0)) # 데이터 셔플용 인덱스 생성

    # 훈련데이터를 랜덤 셔플링된 인덱스 번호를 통해서 재지정 → ※1
    X_ = torch.index_select(X_train, index = indices, dim = 0)
    y_ = torch.index_select(y_train, index = indices, dim = 0)

    # 셔플링 된 데이터를 batch_size로 분리 → 미니 배치를 생성
    X_ = X_.split(batch_size, dim=0)
    y_ = y_.split(batch_size, dim=0)

    # 훈련 손실, 검증 손실 결과를 저장하기 위해 변수 초기화
    train_loss, valid_loss = 0, 0
    # 예측 결과 저장을 위한 빈 리스트 생성 (검증 데이터의 예측 결과 누적)
    y_pred_list = []

    # 학습 ★
    # batch_size로 분리된 X_, y_ 텐서들을 batch_size 개씩 훈련
    for X_i, y_i in zip(X_,y_):
        y_i_pred = model(X_i)
        loss = F.mse_loss(y_i_pred, y_i)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        # 현재 batch_size의 데이터 loss를 더함 → epoch의 loss 결과는 모든 배치마다 loss의 평균
        train_loss += float(loss)

    # 현재 epoch의 loss를 계산 → train_loss 평균
    train_loss = train_loss / len(X_)

    # 검증 ★
    # 학습된 모델을 통해 검증 데이터로 검증(손실 계산) → 역전파 x, 셔플링 x
    with torch.no_grad():
        X_ = X_valid.split(batch_size, dim=0) # 검증 데이터는 셔플링 안 함
        y_ = y_valid.split(batch_size, dim=0)

        # 반복문 (배치): 메모리 문제가 발생하기 때문에 검증도 동일하게 배치를 쪼개서 진행
        for X_i, y_i in zip(X_,y_):
            y_i_pred = model(X_i)
            loss = F.mse_loss(y_i_pred, y_i)

            valid_loss += float(loss)

            # 검증 데이터 배치별 예측값을 리스트에 저장
            y_pred_list.append(y_i_pred)

        # 평균 검증 손실값 계산
        valid_loss = valid_loss / len(X_)

        # 훈련 손실값, 검증 손실값 list에 저장
        train_history.append(train_loss)
        valid_history.append(valid_loss)

        # 학습 과정 출력하기
        if (i+1) % print_interval == 0:
            print(f"epoch: {i+1}, valid_loss: {valid_loss:.4e}, train_loss: {train_loss:.4e}, lowest_loss: {lowest_loss:.4e}")

        # 모델 저장
        # 현재 검증손실값이 지정된 최소손실값보다 작다면? 저장!
        if valid_loss <= lowest_loss:
            lowest_loss = valid_loss
            lowest_epoch = i+1

            # 현재 모델의 가중치를 저장
            best_model = deepcopy(model.state_dict()) # 가중치를 딕셔너리 형태로 가져옴

        # 모델 조기 학습 중단
        else:
            if (early_stop > 0) and (lowest_epoch+early_stop) < i+1:
                print(f"{early_stop} epochs 동안 모델이 개선되지 않음")
                break

print(f"{lowest_epoch + 1} epochs에서 가장 낮은 검증손실값: {lowest_loss}")

# 저장한 best_model 의 가중치를 model에게 로드해주기
model.load_state_dict(best_model)

※1: 순서를 셔플링한 결과를 X_train[indices]로 가져오면 편한데 왜 이렇게 가져오지 않는 걸까?
→ X_train[indices]는 CUDA 오류가 발생할 수 있기 때문
: 텐서 내에서는 GPU 연산을 하다 보니 위와 같은 형식으로 인덱싱을 해서 데이터를 가져오다 보면 오류가 날 위험이 높습니다.

인프런 QnA 답변
PyTorch의 torch.index_select와 인덱싱 연산자인 []를 통한 인덱싱 방법은 매우 비슷한 기능을 제공합니다. 둘 다 텐서에서 특정 인덱스를 기반으로 원하는 요소를 선택하도록 합니다.
그럼에도 불구하고, 코드에서 torch.index_select를 사용하는 특별한 이유가 있다면, 다음과 같은 이유들이 있을 수 있습니다:
1. 명시성: torch.index_select 함수는 선택하려는 차원을 명시적으로 지정해야 합니다. 이는 코드를 읽는 사람에게 해당 연산이 어떤 차원에서 수행되는지 명확히 보여주는 장점이 있습니다. x[indices] 표현식은 암시적으로 첫 번째 차원에서 인덱싱을 수행한다는 것을 가정하므로, 이 점이 명시성에서 약간의 차이를 만들 수 있습니다.
2. 성능: 일부 상황에서 torch.index_select는 [] 연산자보다 약간 더 빠를 수 있습니다. 하지만 대부분의 일반적인 사용 사례에서는 성능 차이는 무시할 수 있을 정도로 작습니다.
3. 호환성: 일부 라이브러리 또는 환경에서는 torch.index_select를 선호할 수 있습니다. 예를 들어, autograd의 역전파 계산이 torch.index_select와 더 잘 작동할 수 있습니다.
그럼에도 불구하고, 주어진 상황에서 torch.index_select(x, 0, indices)와 x[indices]는 동일한 결과를 제공하므로, 어떤 방법을 선택할지는 주로 개발자의 선호도와 스타일에 따라 편하게 사용하시면 됩니다.

해당 내용에 대해 Perplexity가 답변한 내용:

torch.index_select(x, 0, indices) vs. x[indices]

1. 기능적 차이

• torch.index_select(x, dim, indices)
  • 지정한 차원(dim)에서 1D 인덱스 텐서(indices)에 따라 요소를 선택합니다.
  • 반환되는 텐서는 항상 입력 텐서와 동일한 차원을 가지며, 선택한 축만 인덱스의 길이로 바뀝니다.
  • 인덱싱이 한 축에만 국한되므로 다차원 인덱싱을 원할 땐 반복적으로 사용하거나 추가 구현이 필요합니다.
• 고급 인덱싱 (x[indices])
  • 파이썬 스타일의 인덱싱을 사용하여 복수 차원, 불리언 마스크, 다차원 인덱싱 등 더 다양한 인덱스 방법을 지원합니다.
  • 인덱스 형태에 따라 결과 차원이 달라질 수 있습니다.
  • 내부적으로 더 많은 연산이 수행될 수 있어 상황에 따라 성능이 다를 수 있습니다.

2. 성능 차이

• 작은 텐서에서는 torch.index_select가 더 빠르고, 텐서 크기가 커질수록 고급 인덱싱(x[indices])이 더 나은 성능을 보이기도 합니다. 실제로 성능은 인덱스 모양, 반복성 여부, 연산량에 따라 달라집니다.
• index_select는 대체로 간단한 1D 인덱싱에 적합하며, 메모리 사용량 측면에서는 고급 인덱싱이 더 효과적일 수 있습니다.

3. PyTorch에서 torch.index_select와 고급 인덱싱(X_train[indices])의 차이와 CUDA 관련 문제

• 두 인덱싱 방식의 차이
  • torch.index_select
    • 연산 자체가 PyTorch 내부적으로 최적화되어 있어, 지정한 dim에 대해 효율적으로 인덱싱을 수행합니다.
    • 인덱스 텐서는 반드시 1-D LongTensor여야 하며, input, index 둘 다 GPU상(CUDA tensor)이면 완전히 GPU에서 연산됩니다.
  • 파이썬 스타일 고급 인덱싱 (X_train[indices])
    • 파이썬의 NumPy 스타일 고급 텐서 인덱싱(Advanced/Integer Indexing) 기능을 활용하는 방법.
    • 내부적으로 더 많은 복잡성과 부가적인 자료구조 생성, 그리고 일부 경우 추가 메모리 사용을 수반합니다.
    • 때로는 CPU와 GPU 간의 예기치 않은 데이터 이동이 발생할 수 있습니다.
• CUDA 문제(메모리/오류/성능) 이유
  • 파이썬 스타일 고급 인덱싱은 GPU 메모리를 훨씬 더 많이 사용할 수 있습니다. (10배까지 메모리 사용량이 늘어나는 사례도 보고됨 → github)
  • 고급 인덱싱은 새로운 텐서를 만드는데, 이 과정에서 임시 버퍼와 중간 객체가 대량으로 할당되므로, 대규모 데이터셋, 특히 대용량 model에선 CUDA out-of-memory 에러 위험이 높아집니다.
  • torch.index_select는 지정된 차원에서 직접 인덱싱하기 때문에 메모리 효율이 높으며, CUDA에서 추가적인 메모리 복사나 불필요한 장치 간 이동 없이 빠르게 작동합니다.
• 장치 간 이동/호환성 문제
  • 일부 고급 인덱싱 연산 과정에서 인덱스 텐서나 입력 텐서가 GPU와 CPU에 각각 있을 경우 PyTorch가 자동으로 데이터를 CPU에서 GPU로 혹은 그 반대로 이동시킬 수 있으며, 이 과정에서 오류 또는 예기치 않은 동작이 발생할 수 있습니다.
  • 인덱싱에서 텐서가 GPU(CUDA)에 있을 때, PyTorch는 가능한 한 연산을 GPU에서 실행하지만, 고급 인덱싱 구현에 따라 일부 요소가 CPU에서 실행되어 속도가 급격히 저하되거나 오류가 발생하는 케이스가 보고됨.
  • 또, CUDA에서 고급 인덱싱을 사용할 때 인덱스 범위 오류 등은 device-side assert로 매우 불명확한 에러 메시지를 내뱉거나, 정상적으로 예외처리되지 않습니다.
• 결정성 및 일관성
  • 고급 인덱싱은 CPU와 GPU에서 결과가 다르거나 비결정적(non-deterministic)일 수 있습니다. 특히, 동일한 코드가 CPU에서는 매번 같은 결과이지만, GPU에서는 다를 수 있어 디버깅을 어렵게 만듭니다.
• 실전 코드 적용 권장 사항
  • 덜 복잡한 설정에서는 index_select 사용: 메모리 효율, 속도, 에러 처리 등 모든 면에서 안전하게 동작합니다. 입력/인덱스 텐서를 꼭 동일한 장치(GPU) 위에 올려놓으세요.
  • 고급 인덱싱은 작은 텐서, CPU 처리, 특수 목적에만: 대형 텐서나 반복적인 인덱싱이 필요한 상황에서 GPU에서는 피하고, 성능/메모리/디버깅 이슈에 유의해야 합니다.
• 요약:
  • PyTorch에서 X_train[indices]와 같은 고급 텐서 인덱싱은 CUDA 환경에서 비효율적이거나 예기치 않은 메모리 과다 사용, 장치간 데이터 이동, 불명확한 에러 메시지, 결과의 비결정성 등 여러 문제가 발생할 수 있습니다. 반면, torch.index_select는 이런 이슈 없이 GPU에서 안전하고 효율적으로 동작하므로, 대규모 데이터 처리와 DNN 학습 루프에서는 index_select 사용을 권장합니다.
• CUDA 환경에서 x[indices]를 사용할 때 가장 흔한 오류는 device-side assert입니다. 예를 들어, 인덱스가 범위를 벗어나면 CPU에서는 IndexError가 발생하지만, CUDA에서는 불명확한 "device-side assert"나 "CUDA error: device-side assert triggered"라는 메시지가 나올 수 있습니다. 이 경우 실제 오류 원인이 바로 드러나지 않아 디버깅이 어려워질 수 있습니다.
• 또한 인덱싱에 사용하는 텐서와 대상 텐서가 서로 다른 디바이스(CPU vs CUDA)에 있을 때도 오류가 발생할 수 있습니다. 모든 텐서가 동일한 디바이스에 있어야 합니다.

예시: CUDA "device-side assert" 오류 발생 상황

import torch
x = torch.rand(10).cuda()
indices = torch.tensor([11]).cuda()  # 10개 요소밖에 없는데 11번 인덱스 참조
x[indices]  # CUDA error: device-side assert triggered

이 오류는 CPU에서는 IndexError로 명확하게 나오지만, CUDA에서는 애매한 에러 메시지를 뱉습니다. 따라서 디버깅 시 CUDA_LAUNCH_BLOCKING=1를 사용해 동기적으로 에러를 확인하는 것이 좋습니다.

정리

• torch.index_select(x, dim, indices)는 간단하면서도 안전한 인덱싱을 제공하며, 1D 인덱스 및 한 축에만 사용할 때 적합합니다.
• x[indices]는 더 유연하지만(다차원, 불리언, 마스킹 등), 성능 및 직관성 측면에서 상황에 따라 다를 수 있고, 특히 CUDA 환경에서 인덱스가 잘못되거나 device 불일치 시 애매한 CUDA 오류가 발생할 수 있습니다.
• 실수로 인한 범위 초과 인덱싱은 CPU에서는 명확한 에러가 드러나지만, CUDA에서는 디버깅이 까다로워질 수 있으니 주의가 필요합니다.
  참고:
• 인덱싱 변수, 대상 텐서 모두 같은 디바이스에 있어야 하며, 인덱스 범위 초과가 없도록 항상 관리하는 습관을 들이세요.

# 결과 시각화
# 추세 확인을 위해 로그로 스케일링
plt.subplots(figsize=(8,4))
plt.grid()

plt.plot(range(1, len(train_history)+1), train_history, label="train_loss")
plt.plot(range(1, len(valid_history)+1), valid_history, label="valid_loss")

plt.legend()
plt.yscale("log") # 줄어드는 값의 차이가 큰 경우 미세한 변화는 그래프 상 표현이 어려움
plt.show()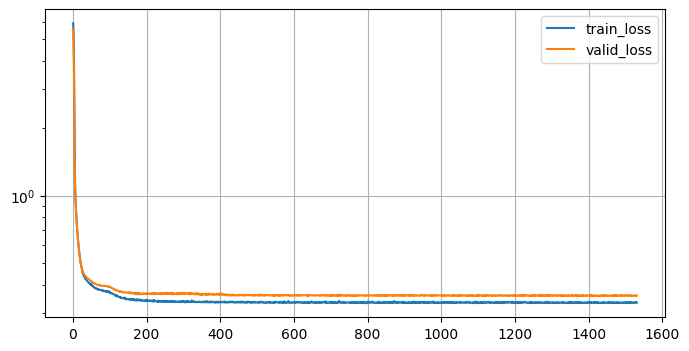

로그(log) 스케일 사용하는 이유

• 값 중 하나가 월등히 크게 되면 다른 값들은 그래프로 차이를 알아보기가 어려움

x_values = [1, 2, 3, 4, 5]
y_values = [10, 1000, 2000, 3000, 1000000000]

plt.figure(figsize=(5, 3))
plt.scatter(x_values, y_values)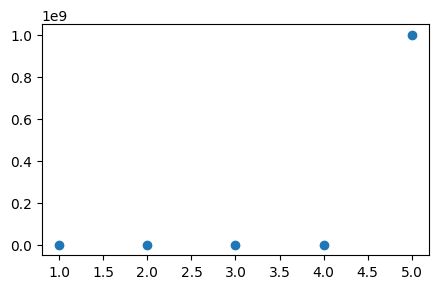

x_values = [1, 2, 3, 4]
y_values = [10, 1000, 2000, 3000]

plt.figure(figsize=(5, 3))
plt.scatter(x_values, y_values)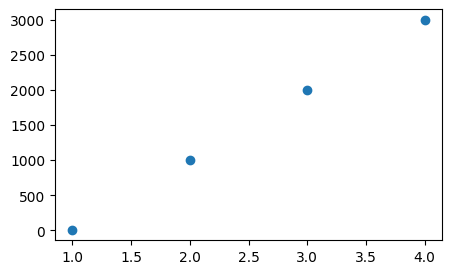

# 로그 스케일 적용을 하면 좀 나아짐: 증가 비율을 그래프로 출력
# 상대적인 비율로 그래프에 출력
x_values = [1, 2, 3, 4, 5]
y_values = [10, 1000, 2000, 3000, 1000000000]

plt.figure(figsize=(5, 3))
plt.yscale("log") # 로그 스케일 적용 → 비율로 볼 수 있음
plt.scatter(x_values, y_values);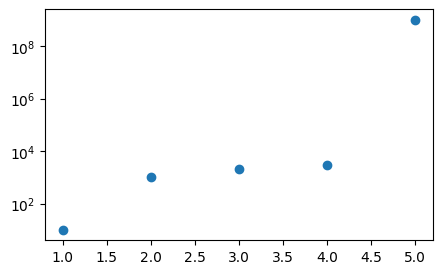

모델 평가

• 테스트 데이터로 평가

test_loss = 0
y_pred = []

with torch.no_grad():
    X_ = X_test.split(batch_size, dim=0)
    y_ = y_test.split(batch_size, dim=0)

    for X_i, y_i in zip(X_,y_):
        y_i_pred = model(X_i)
        loss = F.mse_loss(y_i_pred, y_i)

        test_loss += float(loss)

        # 테스트 데이터 배치별 예측값을 리스트에 저장
        y_pred.append(y_i_pred)

test_loss = test_loss / len(X_)

# 평가 후 예측값들을 하나의 텐서로 병합화여 전체 결과를 확인하기 위해 텐서 병합
y_pred = torch.cat(y_pred, dim=0)

s_his = sorted(zip(train_history, valid_history), key = lambda x: x[1])

print(f"train 데이터의 loss: {s_his[0][0]:.4e}")
print(f"valid 데이터의 loss: {s_his[0][1]:.4e}")

train 데이터의 loss: 3.4322e-01
valid 데이터의 loss: 3.6157e-01

$R^2$ score 확인하기

from sklearn.metrics import r2_score

# 예측값: numpy 변환
y_pred_np = y_pred.detach().cpu().numpy()
# 실제값: numpy 변환
y_test_np = y_test.detach().cpu().numpy()

# r2 score 계산
r2 = r2_score(y_test_np, y_pred_np)
print(f"r2 score: {r2:.4f}")

r2 score: 0.7354

실습: 심층신경망 이진분류

• 유방암 데이터를 활용한 실습 진행

학습목표

• PyTorch를 활용하여 심층신경망을 구성할 수 있다
• 이진분류 신경망을 설계하여 유방암 데이터를 분류할 수 있다.
• 모델 class 설계, 학습, 검증, 시각화, 평가 진행

# 라이브러리 불러오기
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from copy import deepcopy # 데이터를 복사
from tqdm import tqdm

from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

데이터 전처리

# 데이터 불러오기
data_org = load_breast_cancer()

# DataFrame으로 변경
df = pd.DataFrame(data_org.data, columns=data_org.feature_names)
# 정답 데이터 추가
df['target'] = data_org.target

# 데이터 분리(학습, 검증, 평가용 3개로 분리)
data = torch.from_numpy(df.values).float()
X = data[:,:-1]
y = data[:,-1:]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=21)
X_train, X_valid, y_train, y_valid = train_test_split(X_train, y_train, test_size=0.25, random_state=21)

print(X_train.shape, X_test.shape, X_valid.shape)
print(y_train.shape, y_test.shape, y_valid.shape)

torch.Size([341, 30]) torch.Size([114, 30]) torch.Size([114, 30])
torch.Size([341, 1]) torch.Size([114, 1]) torch.Size([114, 1])

# 히스토그램 확인
df.hist(bins=50, figsize=(15, 15))
plt.show()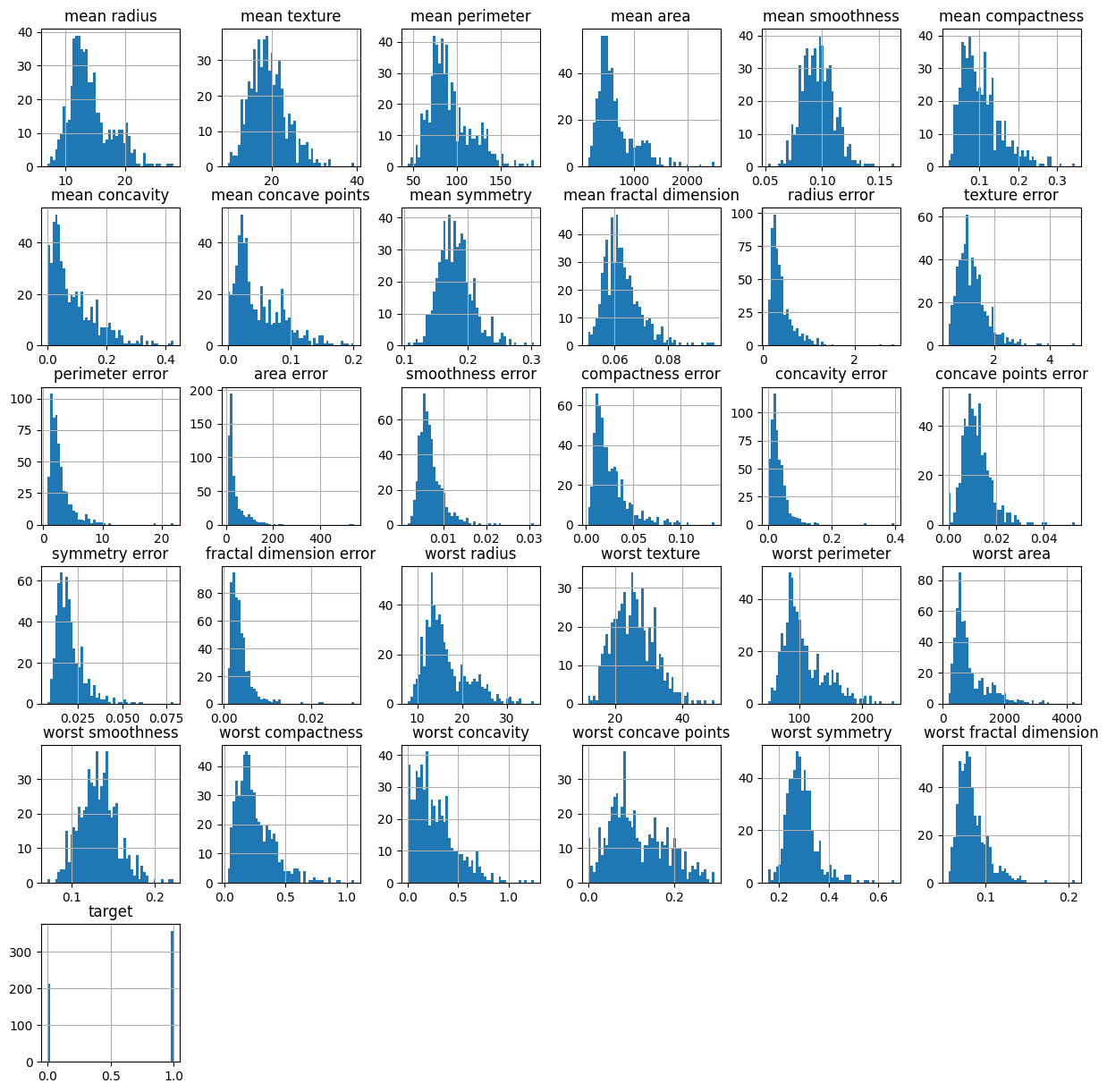

데이터 스케일링

# 스케일링 (X_train, X_test, X_valid)
std_scaler = StandardScaler()
std_scaler.fit(X_train.numpy())
X_train = torch.from_numpy(std_scaler.transform(X_train.numpy())).float()
X_test = torch.from_numpy(std_scaler.transform(X_test.numpy())).float()
X_valid = torch.from_numpy(std_scaler.transform(X_valid.numpy())).float()

심층신경망 설계

• 이진분류 설계

# class 설계 MyModel → nn.Module 부모 클래스 상속
class MyModel(nn.Module):
    # 함수 설계(self, 입력, 출력)
    def __init__(self, input_dim, output_dim):
        super().__init__()
        self.input_dim = input_dim
        self.output_dim = output_dim

        # 신경망 레이어 정의: 5개층(25,20,15,10,5)+출력층
        self.linear1 = nn.Linear(input_dim,25)
        self.linear2 = nn.Linear(25,20)
        self.linear3 = nn.Linear(20,15)
        self.linear4 = nn.Linear(15,10)
        self.linear5 = nn.Linear(10,5)
        self.linear6 = nn.Linear(5,output_dim)
        # 활성화 함수(ReLU, Sigmoid)
        self.act_relu = nn.ReLU()
        self.act_sigmoid = nn.Sigmoid()

    # 연산과정 정의(함수→forward)
    def forward(self, X):
        # 모든 연산층 ReLU, 출력층의 활성화 함수 Sigmoid
        h = self.act_relu(self.linear1(X))
        h = self.act_relu(self.linear2(h))
        h = self.act_relu(self.linear3(h))
        h = self.act_relu(self.linear4(h))
        h = self.act_relu(self.linear5(h))
        y = self.act_sigmoid(self.linear6(h))
        return y

# 모델 객체 생성 → model
model = MyModel(X_train.size(-1), y_train.size(-1))

옵티마이저 생성

# 최적화 함수 선택
optimizer = optim.Adam(model.parameters())

학습 파라미터 및 변수 초기화

# 학습 횟수 및 출력 횟수 지정
n_epochs = 10000
batch_size = 32
print_interval = 10 
early_stop = 100
best_model = None
lowest_loss = np.inf
lowest_epoch = np.inf

신경망 학습 구현: 이진분류

• loss 함수로 F.binary_cross_entropy()를 사용

# 학습 코드 구현: 학습 반복문
train_history, valid_history = [], []

# 1. 반복 학습 (epoch 루프)
for i in tqdm(range(n_epochs)):

    # 2. 훈련 데이터 셔플
    indices = torch.randperm(X_train.size(0))

    # 3. 미니배치로 분할
    X_ = torch.index_select(X_train, dim=0, index=indices)
    y_ = torch.index_select(y_train, dim=0, index=indices)
    X_ = X_.split(batch_size, dim=0)
    y_ = y_.split(batch_size, dim=0)

    # 4. 훈련 
    train_loss = 0
    y_pred = []

    for X_i, y_i in zip(X_, y_):
        y_i_pred = model(X_i)
        loss = F.binary_cross_entropy(y_i_pred, y_i)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        train_loss += float(loss)
        y_pred.append(y_i_pred)

    # 5. 평균 훈련 손실 계산
    train_loss = train_loss / len(X_)

    # 6. 검증 
    with torch.no_grad():
        X_ = X_valid.split(batch_size, dim=0)
        y_ = y_valid.split(batch_size, dim=0)

        valid_loss = 0
        y_pred = []
        
        for X_i, y_i in zip(X_, y_):
            y_i_pred = model(X_i)
            loss = F.binary_cross_entropy(y_i_pred, y_i)
            valid_loss += float(loss)
            y_pred.append(y_i_pred)
        valid_loss = valid_loss / len(X_)
  
        # 7. 손실 기록
        train_history.append(train_loss)
        valid_history.append(valid_loss)
  
        # 8. 진행 상황 출력
        if (i+1)%print_interval == 0:
            print(f"epoch: {i+1}, valid_loss: {valid_loss:.4e}, train_loss: {train_loss:.4e}, lowest_loss: {lowest_loss:.4e}")
  
        # 9. 베스트 모델 저장
        if valid_loss < lowest_loss:
            lowest_loss = valid_loss
            lowest_epoch = i+1
            best_model = deepcopy(model.state_dict())
  
        # 10. 조기 종료 (Early Stopping)
        if (early_stop > 0) and (lowest_epoch + early_stop < i+1):
            print(f"{early_stop} epochs 동안 모델이 개선되지 않음")
            break

# 11. 베스트 모델 복원
model.load_state_dict(best_model)

# 12. 최종 성능 출력
print(f"{lowest_epoch + 1} epochs에서 가장 낮은 검증손실값: {lowest_loss}")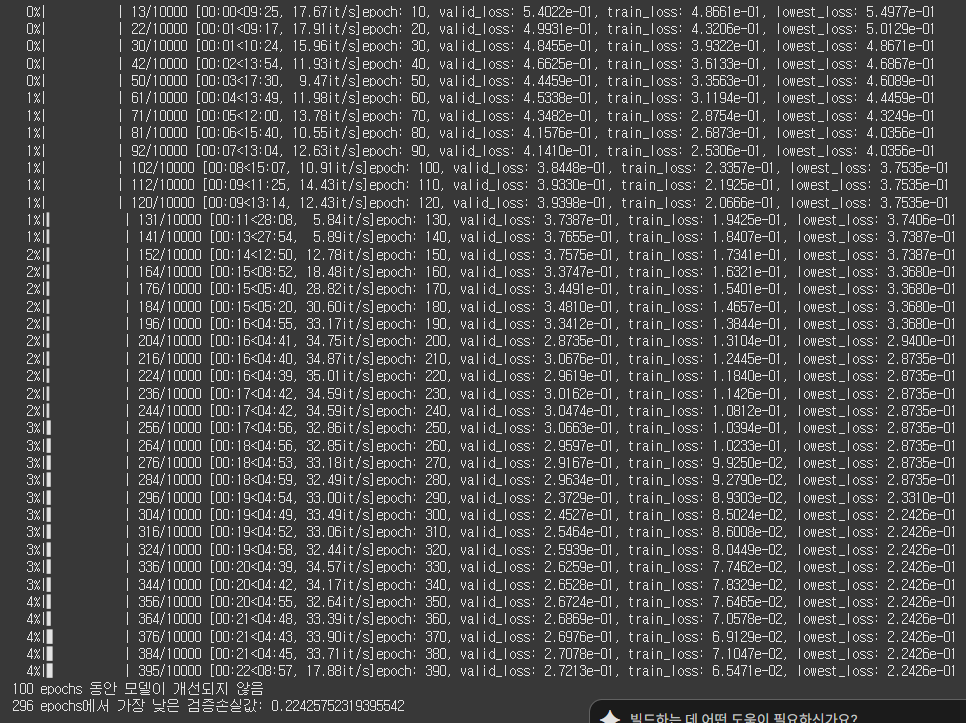

plt.subplots(figsize=(8,4))
plt.grid()

plt.plot(range(1, len(train_history)+1), train_history, label="train_loss")
plt.plot(range(1, len(valid_history)+1), valid_history, label="valid_loss")

plt.legend()
# plt.yscale("log")
plt.show()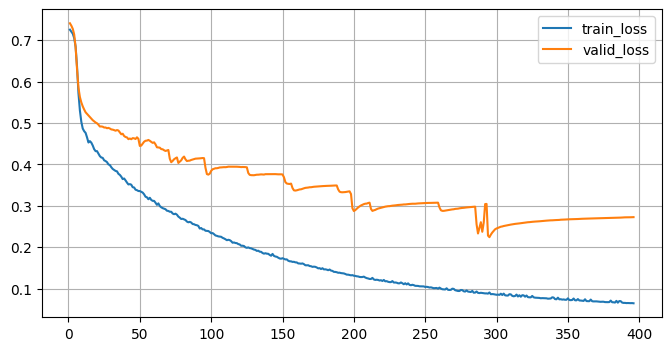

모델 평가

test_loss = 0
y_pred = []

with torch.no_grad():
    X_ = X_test.split(batch_size, dim=0)
    y_ = y_test.split(batch_size, dim=0)

    for X_i, y_i in zip(X_,y_):
        y_i_pred = model(X_i)
        loss = F.binary_cross_entropy(y_i_pred, y_i)

        test_loss += float(loss)

        # 테스트 데이터 배치별 예측값을 리스트에 저장
        y_pred.append(y_i_pred)

test_loss = test_loss / len(X_)

# 평가 후 예측값들을 하나의 텐서로 병합하여 전체 결과를 확인하기 위해 텐서 병합
y_pred = torch.cat(y_pred, dim=0)

s_his = sorted(zip(train_history, valid_history), key = lambda x: x[1])

print(f"train 데이터의 loss: {s_his[0][0]:.4e}")
print(f"valid 데이터의 loss: {s_his[0][1]:.4e}")

train 데이터의 loss: 6.7226e-02
valid 데이터의 loss: 8.0191e-02

from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, confusion_matrix

# 예측값: numpy 변환
y_pred_np = y_pred.detach().cpu().numpy()
# 실제값: numpy 변환
y_test_np = y_test.detach().cpu().numpy()
y_pred_np = np.where(y_pred_np > 0.5, 1. , 0.) #0.5 보다 크면 1., 작으면 0.

# 정확도 계산
accuracy = accuracy_score(y_test_np, y_pred_np)
print(f"accuracy: {accuracy}")

# 정밀도 계산
precision = precision_score(y_test_np, y_pred_np)
print(f"precision: {precision}")

# 재현율 계산
recall = recall_score(y_test_np, y_pred_np)
print(f"recall: {recall}")

# F1-점수 계산
f1 = f1_score(y_test_np, y_pred_np)
print(f"F1-score: {f1}")

# 혼동 행렬 계산 및 시각화
conf_matrix = confusion_matrix(y_test_np, y_pred_np)
print("confusion matrix:\n", conf_matrix)

plt.figure(figsize=(8, 6))
sns.heatmap(conf_matrix, annot=True, fmt="d", cmap="Blues", xticklabels=["negative", "positive"], yticklabels=["negative", "positive"])
plt.xlabel("y_pred")
plt.ylabel("y_test")
plt.title("confusion matrix")
plt.show()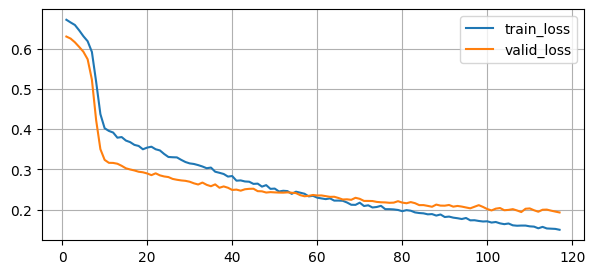

accuracy: 0.9912280701754386
precision: 0.9868421052631579
recall: 1.0
F1-score: 0.9933774834437086
confusion matrix:
 [[38  1]
 [ 0 75]]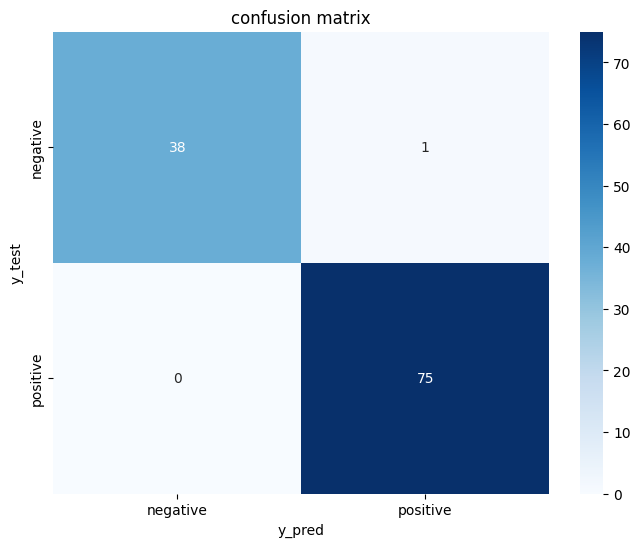

---

---

하루 돌아보기

👍 잘한 점

• 수업 시간에 질문을 많이 했음
• 미니 프로젝트 모델 학습까지 진행
  • 야간자율학습 대신 미니프로젝트 진행해서 평가 및 PPT 초안까지 제작할 예정

👎 아쉬웠던 점

• 학습 코드 구현 과정 중 베스트 모델 저장 및 조기 종료 부분이 아직 완벽하게 이해되지는 않았음
• 미니 프로젝트가 당장 목요일 아침 마감이고 8월 9일에는 정보처리기사 시험도 봐야 해서 당분간 코딩테스트 연습 안 하고 두 가지에 집중하기로 결정한 부분

🔬 개선점

• 학습 코드 구현 관련 내용 찾아서 보충하기
• 코딩테스트 연습 관련해서는 선택과 집중이 더 중요한 것 같아서 계획한 자격증 시험 다 볼 동안은 쉬기로 결정
  • 그래도 혹시나 시간 남거나 자격증 공부하기 싫을 때 한 문제씩 풀기