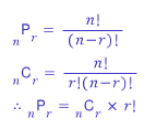[251124] 추가 공부

Suhyeon Lee·2024년 11월 24일
보충 학습
0

자기주도학습

목록 보기
57/83

SQL

여기

성능 관점에서 보는 결합(Join)

성능 관점에서의 서브쿼리(Subquery)

MySQL에서 Pivot table 사용/만들기

  • DB를 조회할 때 종종 행과 열이 바뀌어서 조회가 필요한 경우가 있음 → RDB(관계형 DB)는 행과 열로 이루어져 있는데, 이 위치를 뒤바꾸는 것을 피벗(Pivot)이라고 함
  • Oracle 11g 에서는 해당 기능을 오라클에서 제공하지만, MySQL/MariaDB 는 따로 제공을 하지 않음
    • SQL을 이용하다 보면 이렇게 특정 RDB 제품에서만 지원하는 함수들이 있음

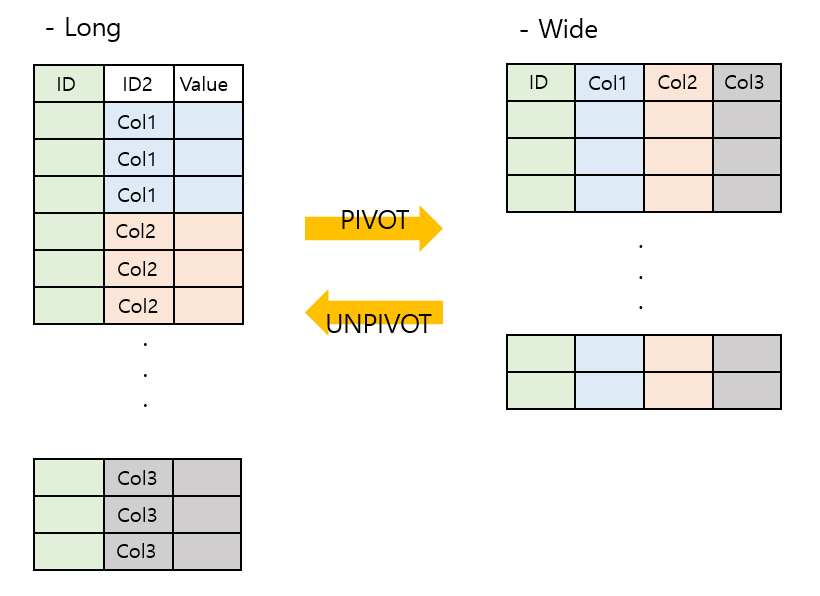
  • PIVOT 함수 없이 pivot을 할 때의 핵심은 CASE WHEN

SQL로 추출한 데이터를 검수하는 과정

  • 추출한 데이터의 Row수가 너무 많다 보니 이것을 눈으로 보면서 제대로 뽑혔는지를 확인할 수 없음
    • 잘못되었지만 추출된 데이터를 가지고 분석을 할 때까지도 잘못된지 모르고 분석을 하다가 되돌아가는 경우가 발생
    • 검수를 하고 싶은데 어떻게 해야 할까? → SQL 쿼리 작성 과정에서 활용할 수 있는 방법

값이 과대집계/과소집계 된 것 같을 때

JOIN을 했던 부분 의심하기

확률통계

경우의 수: 순열과 조합

여기

경우의 수

  • 어떤 사건이 일어나는 경우의 가지 수
    • 동시에 일어나는 경우
      • 곱의 법칙: m x n
    • 동시에 일어나지 않는 경우
      • 합의 법칙: m + n
  • 좀 더 복잡한 경우의 수: 전체 중에서 두 가지 이상의 사건이 일어나는 경우
    • 뽑는 순서를 따질 때/따지지 않을 때
    • 중복을 허락할 때/허락하지 않을 때

예시

여러 가지 색깔의 볼펜 5자루와 연필 3자루가 있을 때

  1. 필기구 한 자루를 선택할 수 있는 경우의 수
    • 8가지
      • 합의 법칙: 5+3
  2. 필기구 두 자루를 선택하는데 볼펜과 연필 각각 한 자루씩 선택하는 경우의 수
    • 15가지
      • 곱의 법칙: 5*3
  3. 필기구 두 자루를 선택하여 배열하는 경우의 수
    • 56가지
      • 순열(Permutation): 8x7
  4. 첫 번째 필기구를 선택하여 사용한 후 제자리에 돌려 놓고(중복 허락) 다시 또 두 번째 필기구를 선택하여 배열하는 경우의 수
    • 64가지
      • 중복 순열: 828^2
  5. 필기구 두 자루를 선택하여 가지는 경우의 수
    • 28가지
      • 조합(Combination): 8×72\frac{8×7}{2}
  6. 필기구 두 자루를 선택하여 가지는데 똑같은 필기구 두 개도 허락하는 경우의 수
    • 36가지
      • 중복 조합: 9×82\frac{9×8}{2}

순열과 조합 이해하기

  • 순열

    nPr=P(n,r)=n!(n−r)!(단,n≥r, 0!=1이고 nP0=1)_nP_r = P(n,r) = \frac{n!}{(n-r)!} \\(단, n≥r,\ 0!=1이고 \ _nP_0 = 1)
    • 순서대로 나열하는 경우의 수
    • 나열의 목적
      • 일어날 수 있는 모든 가짓수를 한 하나도 빠짐없이 보여주기 위한 것
      • 따라서 앞, 뒤의 순서가 다르면 서로 다른 경우의 수
    • 소유보다는 존재(being)!
      e.g. 사과, 배, 귤 중 두 개를 보여주는 경우의 수는 6가지 → (사과, 배), (배, 사과), (사과, 귤), (귤, 사과), (배, 귤), (귤,배)

  • 중복 순열

    nΠr=nr_n\Pi_r = n^r

  • 원 순열

    • 서로 다른 n개 중에서 r개를 뽑아 원형으로 배열하는 방법의 수
      nPrr\frac{_nP_r}{r}
    • 서로 다른 n개의 원소를 원형으로 배열하는 방법의 수
      n!n=(n−1)!\frac{n!}{n} = (n-1)!
      • 처음 앉는 사람은 어디 앉든 똑같기 때문에 1이고 나머지는 그대로 n-1개를 배열하면 되기 때문

  • 조합

    nCr=C(n,r)=n!r!(n−r)!_nC_r = C(n,r) = \frac{n!}{r!(n-r)!}
    • 어떤 것을 묶는 경우의 수
    • 보여주기 위한 나열이 아닌 본격적으로 '선택'하는 경우의 수
      • 가지거나 분배하기 위한 것
      • 앞, 뒤 순서는 상관 없고 다만 무엇을 선택했는지가 중요!
    • 소유(have)와 관계가 깊음
      e.g. 사과, 배, 귤 중 두 개를 가지는 경우의 수는 3가지 → (사과, 배), (사과, 귤), (배, 귤)

  • 중복 조합

    nHr=n+r−1Cr_nH_r = _{n+r-1}C_r

예시

  • 순열

    • 정수 만들기(맨 앞에는 0이 올 수 없음)
    • 인접하여(이웃하여) 배열하기
      • (a+1)!×b!
    • 이웃하지 않도록 배열하기
      • a!×a+1Pba! × _{a+1}P_b
    • 교대로 배열하기
      • m!×n!×2

  • 중복 순열

    • 정수 만들기(같은 숫자의 중복을 허락)
    • 같은 것을 포함한 경우의 수열
      • n!p!×q!×r!\frac{n!}{p!×q!×r!}
    • 최단 거리 길의 수
      • \frac{\(가로+세로)n!}{(가로)!×(세로)!}

  • 원 순열

    • 염주 순열
      • 원순열2\frac{원 순열}{2}
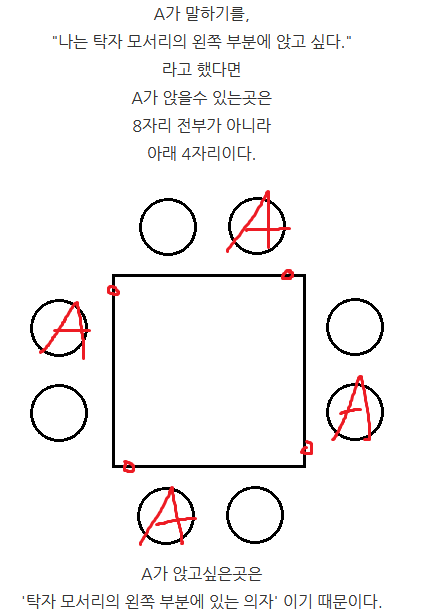
    • 다각형 탁자 순열
      - 원 순열의 수 × 회전할 때 달라지는 자리 개수
      - 원 순열과 달리 처음에 앉는 사람의 경우의 수가 1이 아님(회전시켜서 달라지는 경우가 있음)


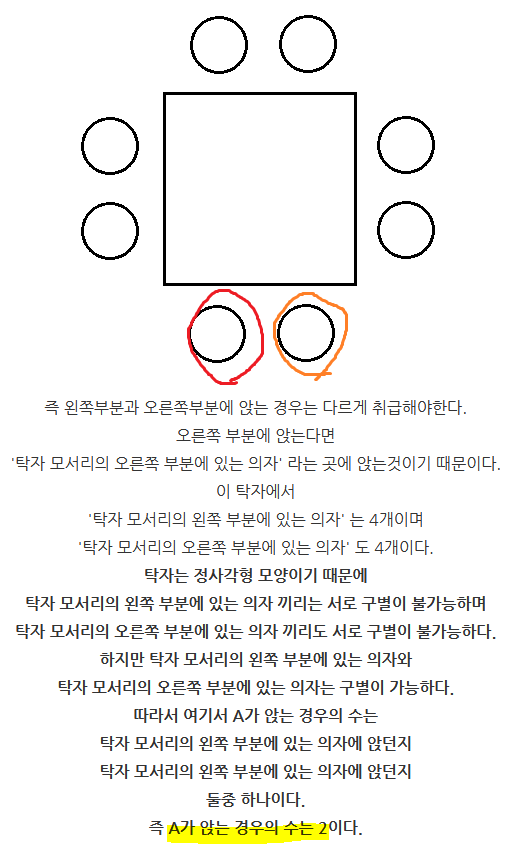
      더 알아보기

  • 조합

    • (총 n개 중 r개를 택하는 순열의 수) ÷ (n개 자체를 배열하는 경우의 수)
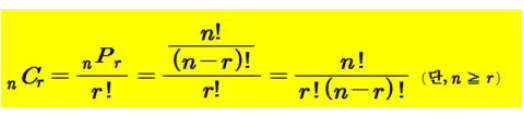
    • n개의 팀 리그전 경기 총 수
      • nC2_nC_2
    • n개의 팀 토너먼트 경기 총 수
      • n-1
        : 토너먼트는 매 경기마다 진 팀은 탈락하고 이긴 팀만 올라가는 방식이기 때문에 최종적으로 우승팀 한 팀만 남게 하려면, 전체 출전 팀에서 한 팀을 빼고 나머지가 탈락하게 되는 만큼의 경기를 치르면 됩니다. 따라서 n-1의 경기를 하면 끝나게 되는 원리입니다.
        토너먼트의 경기 수
    • 선분의 개수
      • nC2_nC_2
    • 직선의 개수
    • 삼각형의 개수
      • 일직선 위에 있지 않은 서로 다른 n개의 점에서 세 점을 잇는 삼각형의 개수: nC3_nC_3
    • 사각형 총 개수

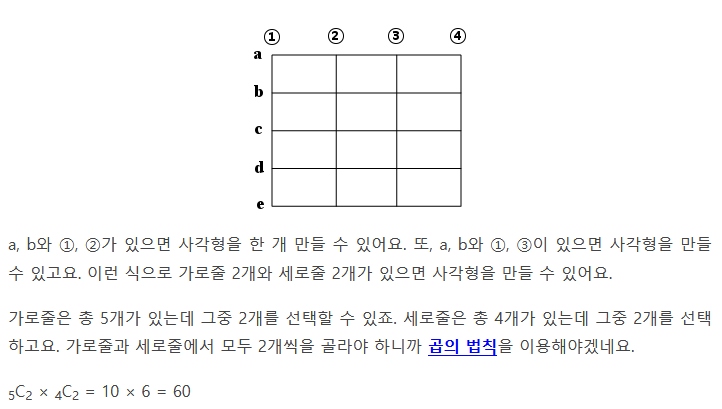
      더 알아보기
    • 조 나누기(서로 다른 n개를 p, q, r개로 분할)
    • 함수의 개수 구하기(차역과 공역 일치, 불일치)

경우의 수 핵심:
순서를 따지는가? 안 따지는가?
중복을 허락하는가? 허락하지 않는가?
확률에서의 '동시에'는 시간적 요소가 아닌 "사건의 연결성"을 의미
경우의 수, 확률에서의 '동시에'는 '두 사건이 연결되어 일어나는'으로 이해

  • 서로 다른 볼펜 5자루 중 2자루, 서로 다른 연필 3자루 중 2자루를 선택(총 4자루)하여 배열하는 방법의 수
    • 5C2×3C2×4!=10×3×24=720_5C_2×_3C_2×4!=10×3×24=720
  • 서로 다른 볼펜 5자루 중 2자루, 서로 다른 연필 3자루 중 2자루를 선택(총 4자루)하는 방법의 수
    • 5C2×3C2=10×3=30_5C_2×_3C_2=10×3=30

첫 번째 문제가 '선택하여 배열'이란 단어 때문에 순열로 보일 수 있지만 정확한 의미는 "일단 선택한 후 다시 배열"입니다.
모든 순열은 조합으로 식을 나타낼 수 있습니다.
→ 볼펜 2자루 선택하고, 연필 2자루 선택해서 모두 4자루를 모은 후 배열하는 4! 곱하기

※ 경우의 수나 확률을 공부함에 있어 가장 첫 출발점은 "또는"과 "그리고"의 구별!

Decision Tree


→ 어떤 경우가 and(곱셈)이고 어떤 경우가 or(덧셈)인지 이해하기!

집에서 학원으로 가는 경우의 수 = 루트1(3×1=3) + 루트2(4×5=20) = 23가지

파이썬으로 순열(Permutation), 조합(Combination)

여기 그리고 여기

  • 파이썬은 permutaion과 combination을 쓸 수 있는 라이브러리를 제공
    • 문자열 리스트도 사용 가능
    • 순열, 조합으로 나온 원소들은 sum() 사용해 더하는 것도 가능
# 순열(Permutations)


    from itertools import combinations, permutations

    nums = [1,2,3,4]
    perm = list(combinations(nums, 2))

# [(1, 2), (1, 3), (1, 4), (2, 1), (2, 3), (2, 4), (3, 1), (3, 2), (3, 4), (4, 1), (4, 2), (4, 3)] 출력


# 조합(Combinations)
from itertools import combinations, permutations

nums = [1,2,3,4]
combi = list(combinations(nums, 2))

# [(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)] 출력

알고리즘 구현: 순열

  • iterable한 sequence 자료형과 선택할 개수 r이 들어왔을 때 각 순열 출력
def permutation(arr, r):
    # 1.
    arr = sorted(arr)
    used = [0 for _ in range(len(arr))]

    def generate(chosen, used):
        # 2.
        if len(chosen) == r:
            print(chosen)
            return
	
	# 3.
        for i in range(len(arr)):
            if not used[i]:
                chosen.append(arr[i])
                used[i] = 1
                generate(chosen, used)
                used[i] = 0
                chosen.pop()
    generate([], used)


>>> permutation('ABCD', 2)
>>> permutation([1, 2, 3, 4, 5], 3)
  1. 먼저 사용자가 원하는 arr 과 r 을 받는다. 그리고 arr 을 오름차순 정렬하는데 여기서는 큰 의미가 있지는 않고 단순히 출력을 이쁘게 하기 위해서이다. 그리고 used 변수를 만드는데, 이 변수는 i 번째 값을 썼는지 저장하는 데 쓰인다. 우리는 모든 순열을 하나씩 만들고 출력하는데 당연히 중복값은 저장되어서는 안 된다.
  2. 실제 순열을 만들 generate 함수를 생성한다. 먼저 chosen 변수는 순열의 원소를 저장되는 변수인데 이 배열에 값을 하나씩 추가하다가 그 개수가 r 이 되는 순간 하나의 순열이 만들어진 것이므로 출력 후 종료한다.
  3. 이 함수의 핵심이다. 모든 순열은 arr 의 0부터 i-1 번째 값으로 시작하기에 for 문으로 다 만들어야 한다. 그리고 chosen 에 값 추가 후, used 에 해당 변수를 사용했다고 체크한다. 그 다음 다시 generate 를 반복한다. 하나가 만들어진 후에는 그 값을 uncheck해줘야 한다.

알고리즘 구현: 조합

  • n 개 중에 r 를 뽑는 조합의 경우의 수
    • 조합(Combination)은 같은 n 개 중에 r 를 뽑되, 순서를 고려하지 않음
def combination(arr, r):
    # 1.
    arr = sorted(arr)

    # 2.
    def generate(chosen):
        if len(chosen) == r:
            print(chosen)
            return

    	# 3.
        start = arr.index(chosen[-1]) + 1 if chosen else 0
        for nxt in range(start, len(arr)):
            chosen.append(arr[nxt])
            generate(chosen)
            chosen.pop()
    generate([])


>>> combination('ABCDE', 2)
>>> combination([1, 2, 3, 4, 5], 3)
  1. 입력은 순열 때와 같다. 배열도 마찬가지로 정렬한다.
  2. 조합을 만드는 generate 함수를 만든다. 순열과 마찬가지로 chosen 에 저장된 아이템 개수가 r 개이면 조합이 하나 완성된 것이기 때문에 값을 출력하고 함수를 종료시킨다.
  3. for 문을 돌리되, 시작을 chosen 에 저장된 마지막 값 다음으로 정한다. 이는 아까 순열함수와 대비되는 부분으로, 조합은 순열과 달리 순서를 고려하지 않고 뽑기 때문에, 가짓수를 제한해줘야 한다. start 가 chosen 이 비어있을 경우 0이 되는 것도 참고한다. 빈값일 때는 그냥 0을 넣어야 한다.

알고리즘 구현: 중복 문제

  • 중복되는 원소에 등장하는 순서를 정하면 해결
    • 예제에서 ‘A’가 두 개면, ‘A’에 보이지 않는 0, 1의 인덱스를 줘서 순서를 지켜서 등장하게 하면 중복이 나오지 않는다.

순열일 때 중복 고려

def permutation(arr, r):
    # 1.
    arr = sorted(arr)
    used = [0 for _ in range(len(arr))]

    def generate(chosen, used):
        # 2.
        if len(chosen) == r:
            print(chosen)
            return
	
        for i in range(len(arr)):
	    # 3.
            if not used[i] and (i == 0 or arr[i-1] != arr[i] or used[i-1]):
                chosen.append(arr[i])
                used[i] = 1
                generate(chosen, used)
                used[i] = 0
                chosen.pop()
    generate([], used)


>>> permutation('AABC', 2)


['A', 'B']
['A', 'C']
['B', 'A']
['B', 'C']
['C', 'A']
['C', 'B']
  • i 가 0일 때:
    • i 가 0이면 배열의 첫 원소이기 때문에 바로 쓰면 된다.
  • arr[i-1] != arr[i] 일 때:
    • 지금은 arr 이 정렬되어 있다. 이때 i 번째 원소가 i-1 번째와 다르면 그냥 ‘B’, ‘C’ 처럼 서로 다른 원소이기 때문에 바로 쓴다.
  • used[i-1] 일 때:
    • 가령 i 번째 원소가 두 번째 ‘A’이면, 중복을 피하기 위해 첫 번째 ‘A’가 사용된 상태여야만 쓸 수 있다. 그래서 i-1 번째 원소가 쓰인 상태인지 확인한다.

조합일 때 중복 고려

def combination(arr, r):
    # 1.
    arr = sorted(arr)
    used = [0 for _ in range(len(arr))]

    # 2.
    def generate(chosen):
        if len(chosen) == r:
            print(chosen)
            return

    	# 3.
        start = arr.index(chosen[-1]) + 1 if chosen else 0
        for nxt in range(start, len(arr)):
            if used[nxt] == 0 and (nxt == 0 or arr[nxt-1] != arr[nxt] or used[nxt-1]):
                chosen.append(arr[nxt])
                used[nxt] = 1
                generate(chosen)
                chosen.pop()
                used[nxt] = 0
    generate([])


>>> combination('ABCDE', 2)
>>> combination([1, 2, 3, 4, 5], 3)

추가

# 리스트에서 나열할 수 있는 모든 경우의 수
input_list = [1,2,3,4,5]
used = [0]*len(input_list)

print(used)

def perm(arr, n):
    if n == len(input_list):
        print(arr)
        return
    for i in range(len(input_list)):
        if not used[i]:
            used[i] = 1
            arr.append(input_list[i])
            perm(arr, n+1)
            arr.pop()
            used[i] = 0

perm([], 0)

# 리스트에서 뽑을 수 있는 모든 경우의 수
nums = [1, 2, 3, 4, 5]

answer_list = []

def combi(n, ans):
    if n == len(nums):
        temp = [i for i in ans]
        answer_list.append(temp)
        return
    ans.append(nums[n])
    combi(n + 1, ans)
    ans.pop()
    combi(n + 1, ans)

combi(0, [])
print(answer_list)

# 리스트에서 r개의 값을 나열할 수 있는 경우의 수
nums = [1, 2, 3, 4, 5]
answer_list = []

def nCr(n, ans, r):
    if n == len(nums):
        if len(ans) == r:
            temp = [i for i in ans]
            answer_list.append(temp)
        return
    ans.append(nums[n])
    nCr(n + 1, ans, r)
    ans.pop()
    nCr(n + 1, ans, r)

nCr(0, [], 3)
print(answer_list)

임베딩(Embedding)

  • 사람이 사용하는 언어나 이미지는 0과 1로만 이루어진 컴퓨터 입장에서 그 의미를 파악하기가 어려움

    • 예: 인간의 자연어는 수치화되어 있지 않은 데이터이기 때문에 특징을 추출해 수치화를 해줘야 함 → word embedding
      • 사람이 쓰는 자연어를 기계가 이해할 수 있는 숫자의 나열인 벡터로 바꾼 결과 혹은 그 과정 전체 == 임베딩

  • 임베딩은 다른 딥러닝 모델의 입력값으로 자주 쓰이고 품질 좋은 임베딩을 쓸수록 모델의 성능이 좋아짐

    • 임베딩을 다른 딥러닝 모델의 입력값으로 쓰는 기법 == 전이 학습
      • 전이 학습은 사람이 학습하는 방식과 비슷: 살면서 쌓아 온 지식을 바탕으로 새로운 사실을 이해하고 학습(0부터 시작하지 않음)

  • 임베딩의 품질이 좋을수록 수행하려는 태스크의 성능이 올라가고 학습 손실도 적고 빠르게 감소하여 모델의 수렴이 빨라짐

    • 즉, 품질이 좋은 임베딩을 쓰면 원하는 모델을 빠르고 효율적으로 학습할 수 있음

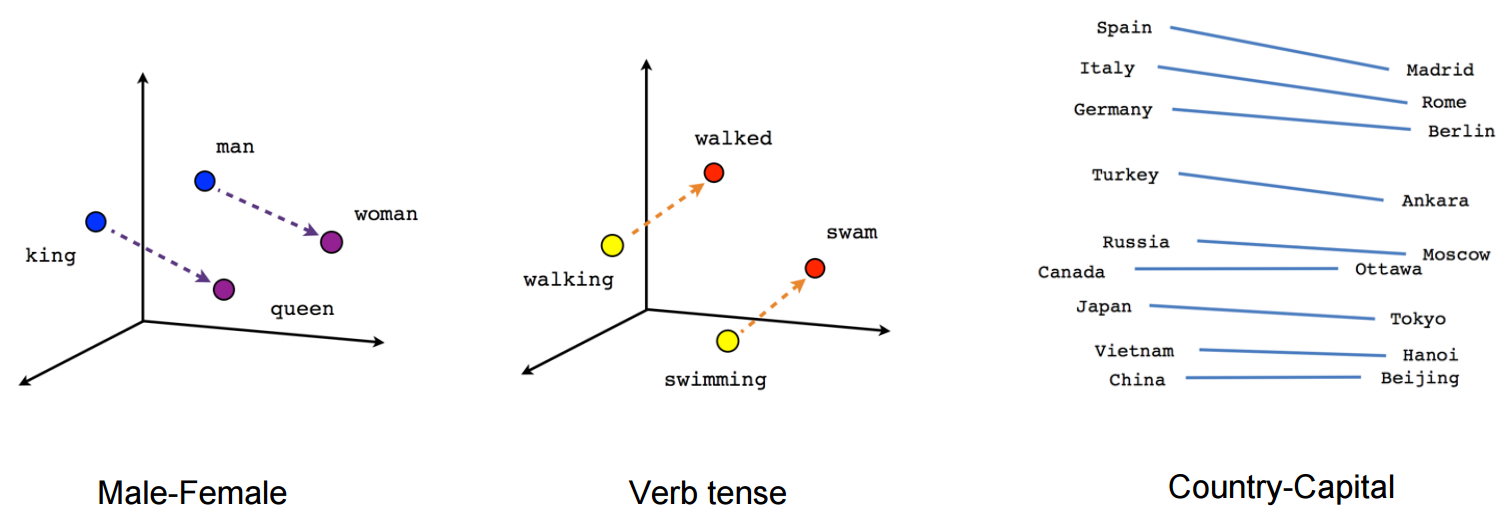
  • 높은 차원의 데이터로 인해 생기는 비효율성과 특징을 나타내기 어렵다는 단점으로 인해 임베딩을 수행하는데, 이 때 저차원의 밀집행렬(Dense Matrix)를 사용

    • 임베딩 벡터
      • 밀집행렬로 임베딩된 벡터는 각 요소에서 단어의 서로 다른 특성을 나타냄
      • 각 요소에는 단어가 관련 특성을 대표하는 정도를 나타내는 0~1 사이의 값이 포함
      • 즉, 임베딩을 통해 텍스트를 단순히 '구분' 하는것이 아닌 의미적으로 '정의'하는 것

  • 'The squad is ready to win the football match'
  • 'The team is prepared to achieve victory in the soccer game'
    위의 두 문장은 의미는 같지만 비슷한 단어가 거의 없음 → 하지만 각 문장의 임베딩 벡터에서는 의미적 인코딩이 매우 유사하기 때문에 임베딩 공간에 서로 가까이 놓임!
profile
Suhyeon Lee
2 B R 0 2 B
이전 포스트

2024-11-24

다음 포스트

[261124] 추가 공부

0개의 댓글

관련 채용 정보