f1-score 종류와 의미

• scikit-learn의 classification_report
  • 분류 모델의 예측 성능을 평가하기 위해 널리 활용
    
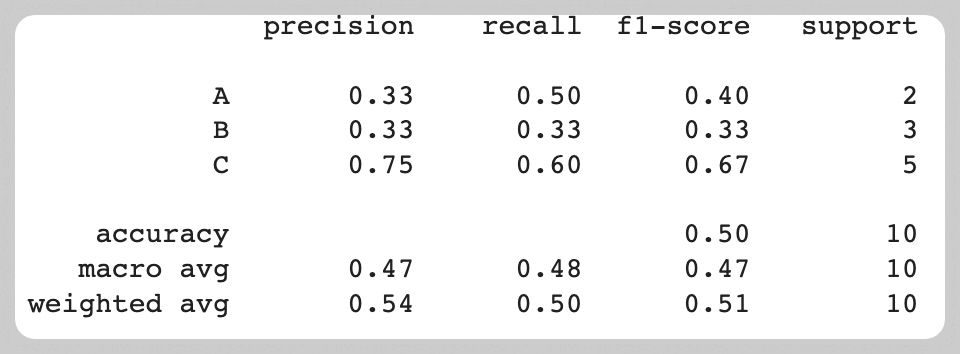
    • 이진 분류일 때는 주로 소수의 클래스에 해당하는 percision, recall, f1-score를 중요하게 봄

f1-score의 종류

1. macro average
   • averaging the unweighted mean per label
   • 라벨별 f1-score를 산술평균한 것
2. weight average

• averaging the support-weighted mean per label
• 라벨별 f1-score를 샘플 수(support)의 비중에 따라 가중 평균한 것

3. micro average

• averaging the total true positives, false negatives and false positives
• 전체 TP, FN, FP를 평균한 것
• 다중 분류에서 정확도와 같음

f1-score의 계산: 다중 분류

• 3종류의 라벨을 가진 10개의 샘플 y_true (리스트)와 각 샘플에 대응하는 예측값 y_pred 가 있다고 가정한 뒤, 성능을 평가하기 위해 precision 과 recall 을 계산하고, 둘의 조화 평균인 f1-score 를 계산

y_true = ["A", "A", "B", "B", "B", "C", "C", "C", "C", "C"]
y_pred = ["A", "B", "A", "B", "C", "A", "B", "C", "C", "C"]

• confusion matrix
  

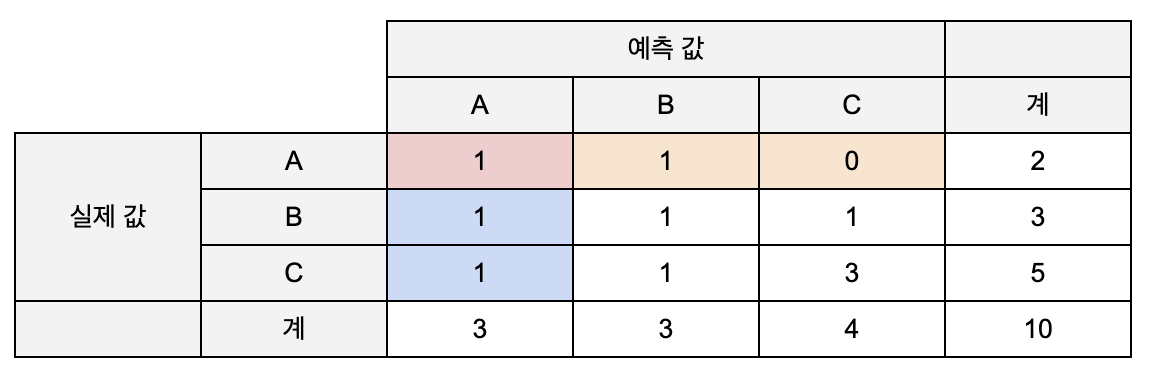
• confusion matrix 를 기반으로 각 라벨에 대한 precision, recall, f1-score 를 계산

  • A를 A로 예측한 건수는 1개 (TP), A가 아닌 것을 A로 예측한 건수는 2개 (FP), A를 A가 아닌 것으로 예측한 경우는 1개 (FN)
    • precision(= TP/(TP+FP))은 A로 예측한 건 중 실제 A인 건의 비율이므로 0.33, recall(= TP/(TP+FN))은 실제 A 중 A로 예측된 건의 비율이므로 0.5으로 계산된다. 이를 토대로 A에 대한 f1-score( = 2(precision x recall)/(precision+recall))는 0.4임을 알 수 있다.

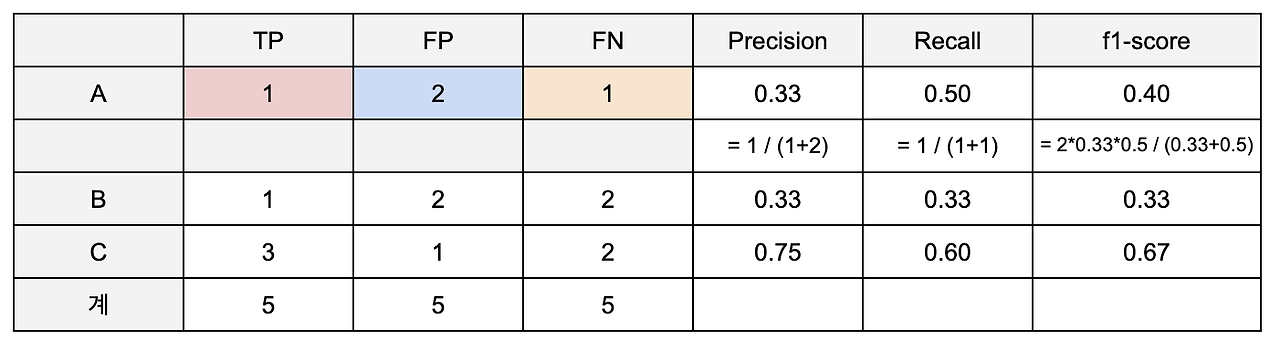
• macro, weighted, micro average f1-score 를 각각 계산해보면:
  • macro average
    • 단순히 A, B, C 라벨에 대한 f1-score 를 평균한 값
    • f1-score (macro) = ( 0.4 + 0.33 + 0.67) / 3 = 0.47
  • weighted average
    • A, B, C 라벨의 개수에 비례하게 가중치를 줘서 f1-score 를 평균한 값
    • f1-score (weighted) = (0.4)(0.2) + (0.33)(0.3) + (0.67)*(0.5) = 0.51
  • micro average
    • 전체 샘플에 대해 종합적으로 f1-score 를 계산
    • precision = 5 / (5+5) = 0.5
      recall = 5 / (5+5) = 0.5
      f1-score (micro) = 2(0.5)(0.5) / (0.5+0.5) = 0.5
      → accuracy와 f1-score(micro)의 값이 같음

micro averge

• 결론부터 말하면, 다중 분류에서 micro 평균을 적용한 recall, precision, accuracy는 동일

  • recall과 precision이 동일하므로 둘의 평균인 f1-score 도 동일한 값을 가짐

• 해당 지표들이 동일한 값을 가지는 원인을 알아보기 위해 수식을 통해 확인해보자
  

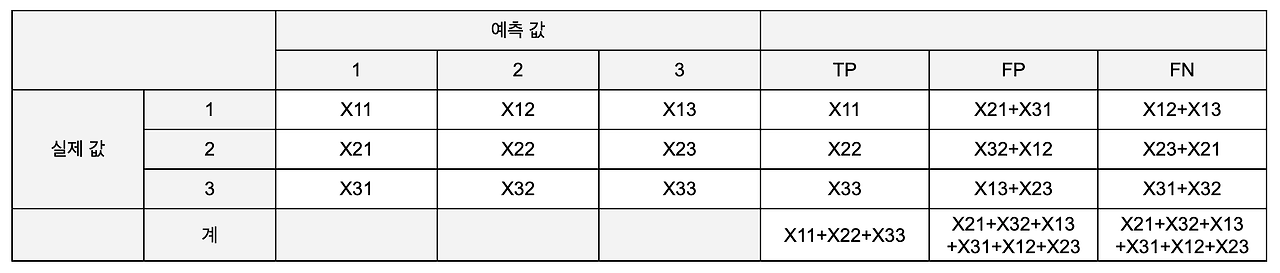
  • $X_{ij}$ (i, j = 1, 2, 3)
    • 실제 i를 j로 예측한 개수
  • micro average 성능 지표를 계산하기 위해 TP, FP, FN 각각의 총합을 계산해보면:
    • TP 의 총합: $X_{11}+X_{22}+X_{33}$
    • FP, FN 의 총합: 표의 나머지 값들을 다 더한 값($X_{21}+X_{32}+X_{13}+X_{31}+X_{12}+X_{23}$)

• FP와 FN의 총합이 같으므로 precision과 recall은 동일함
  또한, TP+FP 및 TP+FN이 전체 모수를 나타내므로 precision, recall 과 accuracy가 동일한 값을 가짐

• 그러므로 classification report를 출력했을 때 micro avg가 아닌 accuracy 하나의 값만 표현

결론

• 라벨의 중요도에 따라 어떤 지표를 선택할지가 달라짐
  • 모든 라벨이 유사한 중요도를 가진다면 macro average 값을 참고
  • 샘플이 많은 라벨에 중요도를 두고 싶다면 weighted average 값을 참고
  • 라벨에 상관없이 전체적인 성능을 평가하고 싶을 때는 micro average, 즉 accuracy 를 활용

Clustering(군집화)

• Unsupervised learning(비지도 학습) 중 하나인 Clustering(군집화)
  • 학습 데이터에 대해 label이 주어지지 않은 경우

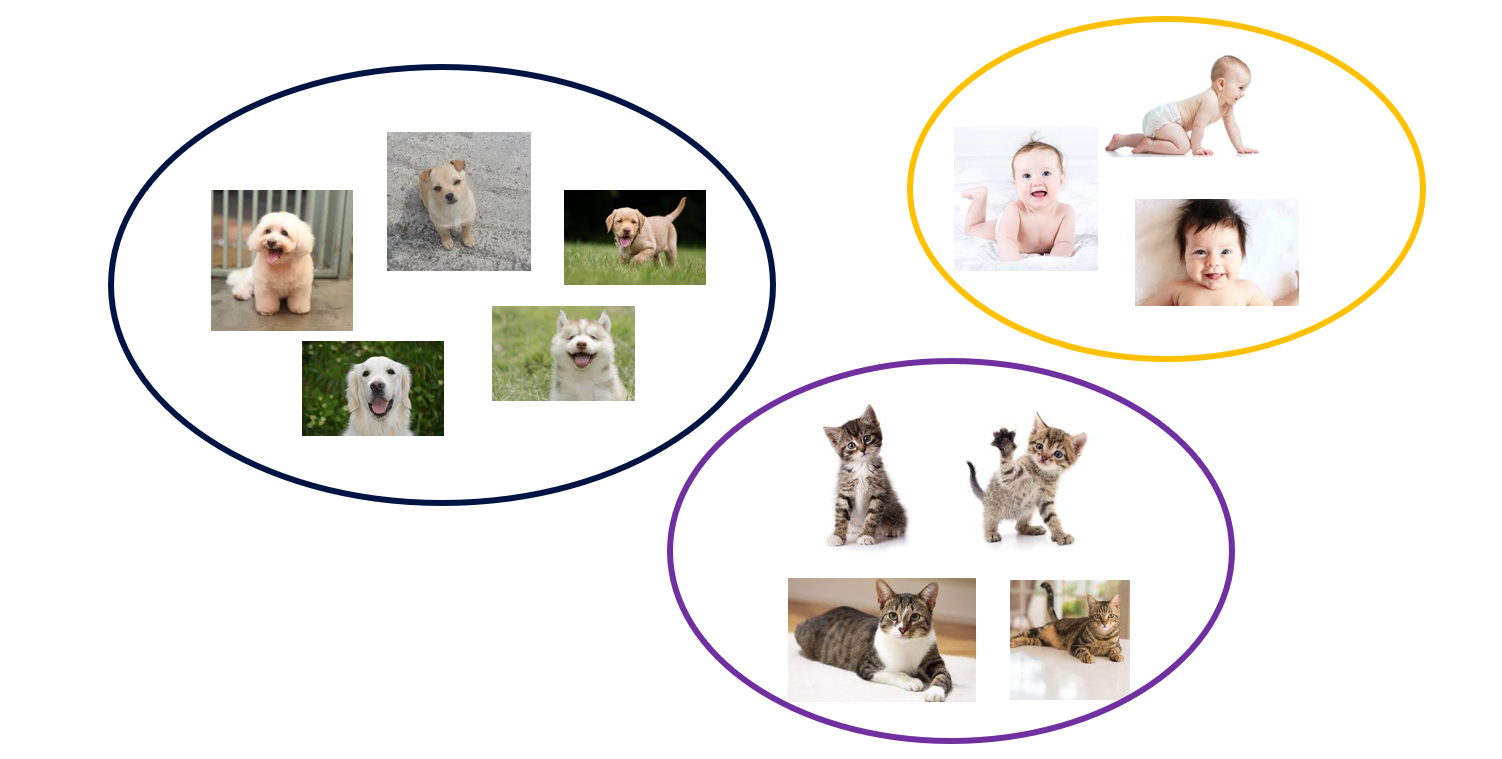
• 위와 같이 사진이 있다고 할 때, 우리는 각 이미지의 유사한 정도를 바탕으로 몇 개 그룹으로 나눌 수 있음
  • 3개 그룸: 개, 고양이, 아기
    
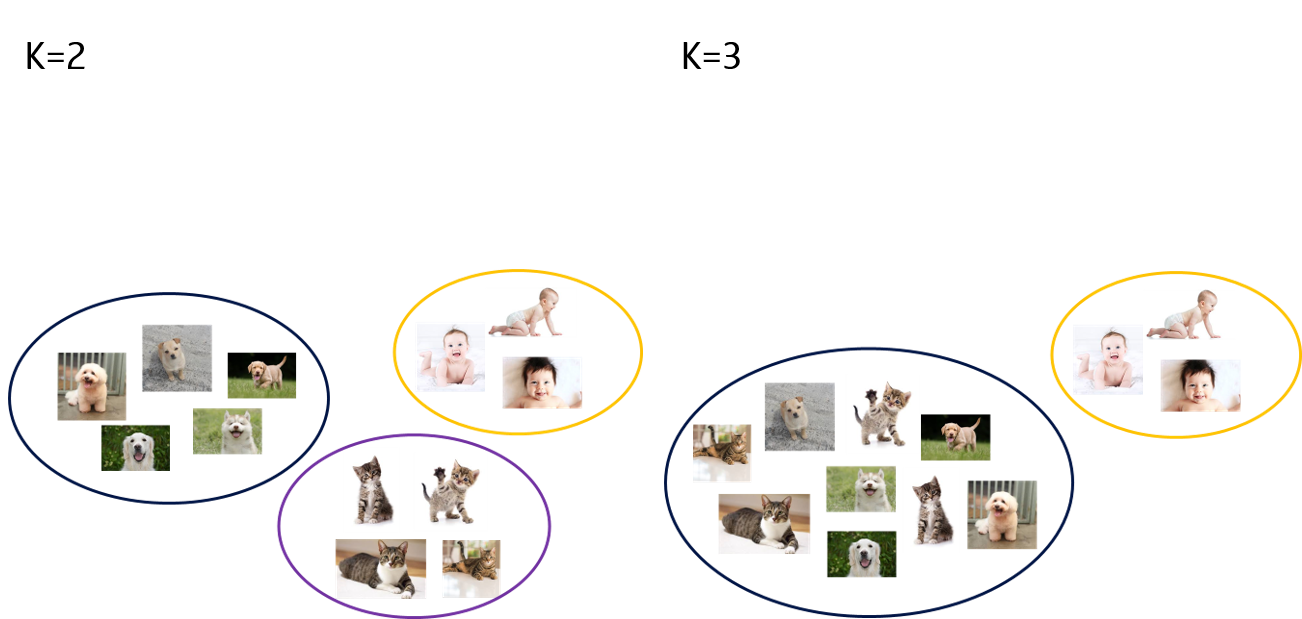
  • 2개 그룹: 사람 대 반려동물
    

→ 즉, 비지도 학습에는 완벽한 정답이 존재하지 않음!

• 비지도학습의 대표적인 예인 Clustering은 주어진 데이터를 몇 개 그룹(Cluster)으로 분리
  • 이때 Cluster간 데이터의 분산은 최대화시키고, Cluster 내 데이터의 분산은 최소화시키는 방향으로 학습
  • 그렇다면 적절한 그룹의 수 k는 어떻게 정할까?
    

Evaluation metrics

• Clustering에 사용되는 평가 지표가 별도로 존재
  cf. 분류 모델에 사용되는 지표

• 데이터 간 거리 (Distance)나 클러스터의 직경 (Diameter) 또는 분산 (Variance)를 이용한 지표

Dunn index

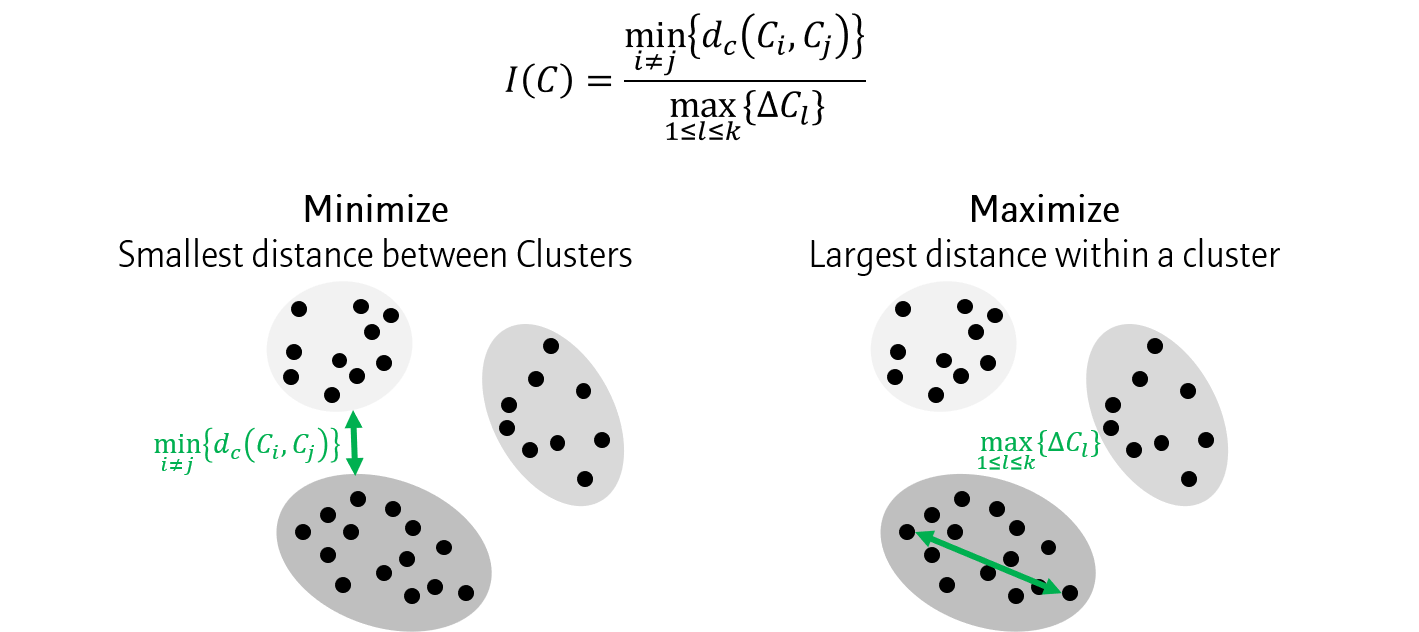
• 클러스터간 거리 중 최소값과 클러스터내 거리 중 최대값의 비율

Silhouette

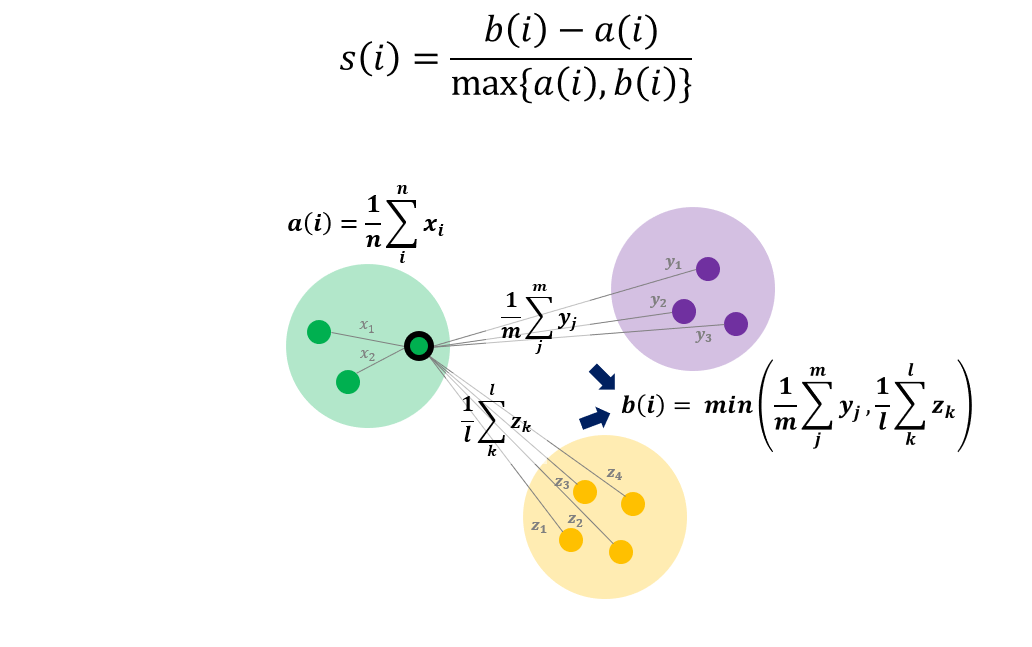
• Silhouette 지표
  $s(i)=\frac{b(i)-a(i)}{max(a(i),b(i))}$
  • $a(i)$: 클러스터 내 거리의 평균값
  • $b(i)$: 클러스터 간 거리의 평균값 중 최소값
  • Silhouette $s(i)$는 -1부터 1까지의 값을 가짐

• Worst case
  • 클러스터를 구분할 수 없을 정도로 군집화가 안 됐을 때
    • 클러스터간 거리가 모두 0이 되기 때문에 $b(i)=0$
    • 따라서 $s(i)=−1$의 값을 가짐
• Best case
  • 각 클러스터 내 모든 점들이 한 점에 모여있는 상태
    • 클러스터 내 거리가 0이 되기 때문에 $a(i)=0$
    • 따라서 s(i)=1의 값을 가짐

더 알아보기

하드 클러스터링과 소프트 클러스터링

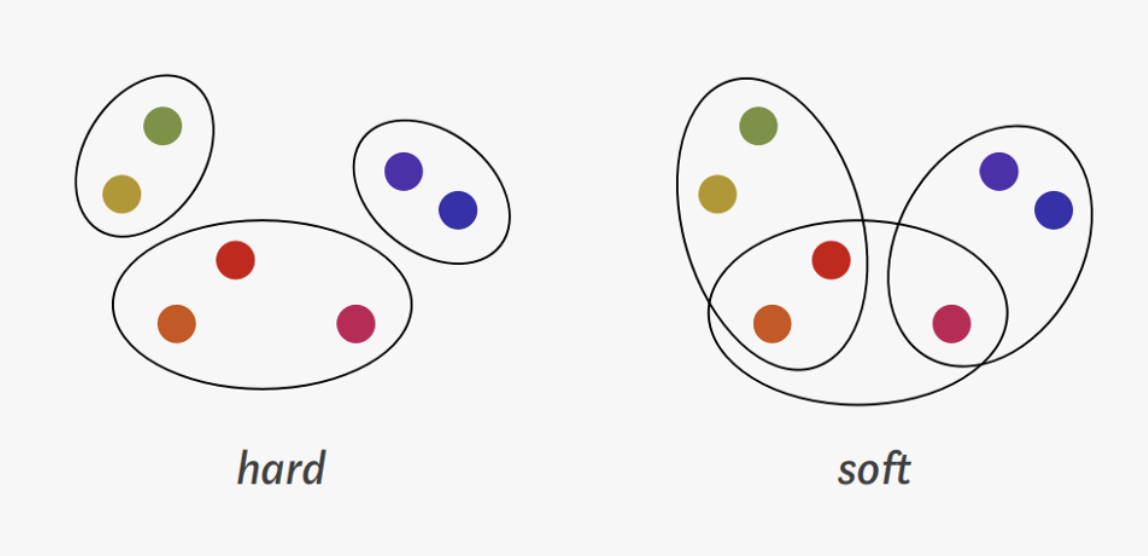
하드 클러스터링(Hard clustering)

• 하나의 데이터를 정확히 하나의 군집에 할당하는 것
  • 각 데이터가 한 cluster에만 속하는 경우
• hierarchical clustering, k-means clustering, dbscan, optics

소프트 클러스터링(Soft clustering)

• 하나의 데이터를 다수의 군집에 할당하는 것
  • 각 데이터가 여러 cluster에 속하는 경우
• Fuzzy clustering, topic models, fcm, soft k-means

Partitional VS Hierarchical clustering

Partitional clustering

• 모든 데이터를 한번에 분류하는 방법
  (예) K-means clusterin

Hierarchical clustering

• 가까운 데이터부터 단계적으로 분류해나가는 방법
  (예) Hiearchical clustering

🡆 K-means clustering은 Hard clustering이자 Partitional clustering임