머신 러닝 특강: 회귀 분석

Suhyeon Lee·2024년 11월 27일
라이브 세션
0

라이브 세션

목록 보기
29/37

회귀란 무엇인가?

기본 개념 소개

회귀(Regression)

  • 데이터를 기반으로 연속적인 값을 예측하는 머신러닝 기법

단어의 유래

  • 한자

    • 回(돌다 회)
      • 다시 돌아온다는 뜻을 가짐
    • 歸(돌아갈 귀)
      • 본래 자리로 돌아간다는 뜻을 가짐
    • "회귀"라는 단어는 "다시 돌아간다"는 의미를 가지고 있음
      • 통계학에서 사용되는 회귀 분석(regression)의 초기 개념에서 파생됨

  • 통계학에서의 어원

    • "regression(회귀 분석)"은 영국의 통계학자 프랜시스 골턴(Francis Galton)에 의해 처음 사용: 19세기 후반 골턴이 부모의 키와 자식의 키 간의 상관관계를 연구하면서 등장
      • 부모가 평균보다 키가 크더라도, 자식의 키는 평균으로 "되돌아가는(regress)" 경향을 보임
      • 반대로, 부모가 평균보다 키가 작더라도 자식의 키는 다시 평균으로 "되돌아가는" 경향을 보임
    • 골턴은 이를 "regression to the mean"(평균으로의 회귀)라고 부름
    • 이후 이 개념이 확장되어, 데이터의 변수 간 관계를 모델링하여 하나의 변수(종속 변수)가 다른 변수(독립 변수)에 대해 변화하는지를 분석하는 기법으로 발전
      • 하나의 변수(단순선형회귀) → 확장해서 여러 개의 변수를 다룰 수도 있어요!(다중회귀)

→ 경향성 분석, 경향 예측

분류와의 차이점

  • 분류는 범주(categorical) 예측, 회귀는 수치(numerical) 예측

→ continuous(연속형) vs. discrete(이산형)

날씨 예측

  • 회귀
    • 내일의 정확한 기온(예: 22.5°C)을 예측
    • 목표
      • 연속적인 숫자 예측
  • 분류
    • 내일 날씨가 맑음, 흐림, 비 중 어떤 상태인지 예측
    • 목표
      • 정해진 범주 중 하나 선택

주식 시장

  • 회귀
    • 특정 회사의 주식 가격이 다음 날 몇 원(예: 101,500원)이 될지 예측
    • 목표
      • 가격처럼 연속된 값을 예측
  • 분류
    • 특정 주식이 오를지, 내릴지(상승/하락) 예측
    • 목표
      • 상승/하락이라는 두 가지 범주 중 하나 선택

부동산

  • 회귀
    • 서울 강남의 특정 아파트의 매매가(예: 15억 원)를 예측
    • 목표
      • 정확한 수치로 나타나는 가격 예측
  • 분류
    • 강남의 특정 아파트가 "고급", "보통", "저렴" 중 어느 등급에 해당하는지 분류
    • 목표
      • 등급(범주)으로 분류

의료 데이터

  • 회귀
    • 환자의 체질량지수(BMI)를 기준으로 예상 혈압 수치(예: 120/80 mmHg)를 예측
    • 목표
      • 혈압처럼 연속적인 값을 예측
  • 분류
    • 환자가 고혈압인지 정상인지(고혈압/정상) 분류
    • 목표
      • 진단을 위해 특정 범주로 나눔

교육

  • 회귀
    • 학생의 학습 시간에 따라 예상 점수(예: 87점)를 예측
    • 목표
      • 시험 점수와 같은 연속적인 값 예측
  • 분류
    • 학생이 시험에서 "합격"인지 "불합격"인지 예측
    • 목표
      • 합격/불합격이라는 두 가지 범주로 분류

고객 데이터 분석

  • 회귀
    • 고객이 다음 달에 소비할 예상 금액(예: 50만 원)을 예측
    • 목표
      • 금액처럼 연속적인 값 예측
  • 분류
    • 고객이 다음 달에 "구매할지" 또는 "구매하지 않을지"를 예측
    • 목표
      • 구매/비구매라는 두 가지 범주로 분류
구분회귀분류
출력연속적인 수치 값(실수)정해진 범주(이산적 값)
예시 질문"얼마나?"(기온, 가격, 점수)"어떤?"(상승/하락, 합격/불합격)
대표 알고리즘선형 회귀, 다항 회귀, 트리기반모델 등로지스틱 회귀, SVM, 트리기반모델 등

수학적 배경

  • 입력 X와 출력 Y 사이의 관계

→ 머신 러닝도 결국 크게 보면 하나의 함수라고 생각할 수 있어요!(x를 넣으면 y가 나옴)



선형 회귀 모델의 기본 원리

선형 회귀란?

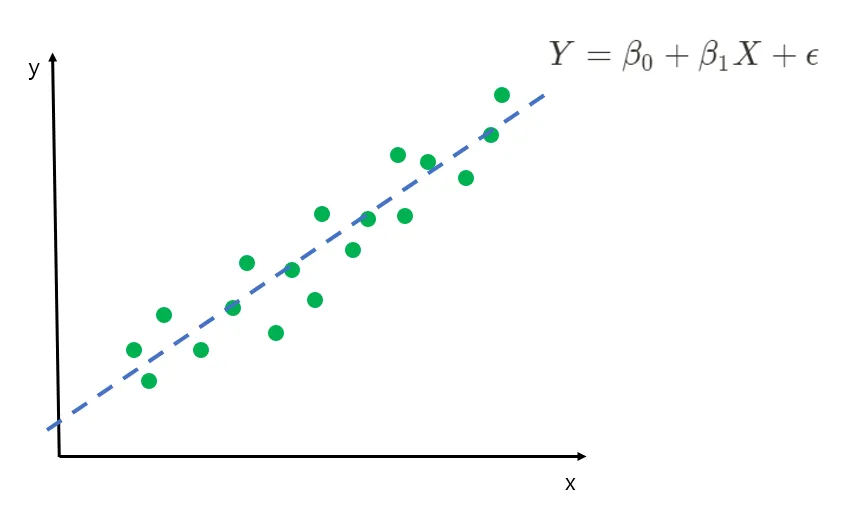
  • 독립 변수(입력) X와 종속 변수(출력) Y 사이의 선형 관계를 학습하는 모델
  • 직선 방정식
    • Y=WX+b (실제로는 오차가 있을 수 있음으로 오차를 어느정도 고려함 → ϵ\epsilon)

단순선형회귀 vs. 다중회귀

  • 만약 독립변수(X)가 여러 개라면?

    • 다중회귀를 사용! (다중회귀도 선형회귀의 일종임)

    → 평면도 직선이라고 볼 수 있기 때문

  • 비교
구분단순선형회귀다중회귀(선형회귀)
독립 변수의 개수1개2개 이상
방정식 형태y=Wx+by=W1​x1​+W2​x2​+⋯+b
시각화2D (직선)3D 이상 (평면 또는 초평면)
모델 복잡도낮음상대적으로 높음

※ 선형 회귀: 경향성을 확인할 수 있으면서 오차를 최소화하는 직선(또는 평면)을 찾는 것

모델 학습 과정

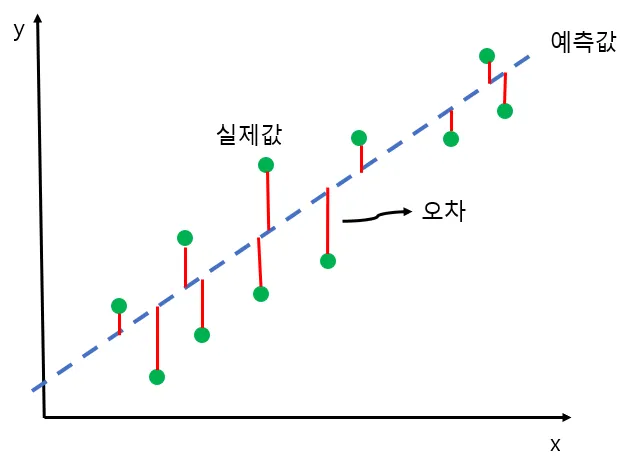
  • 손실 함수(오차): 평균 제곱 오차(MSE; Mean Squared Error)
    • 예측값과 실제값의 차이(오차)를 제곱해서 평균을 구한 값
    • 실제 데이터와 예측 데이터 편차의 제곱합인 오차제곱합(SSE)를 데이터의 크기로 나눠 평균을 만드는 것이 평균 제곱 오차(SSE/(df-1))
  • 최적화: 수학적인 방법 or 경사하강법(Gradient Descent) 사용
    • 수학적인 방법
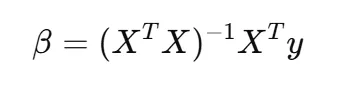
      • 오차를 최소화 하는 계수를 찾는 방법인 ‘최소자승법(Ordinary Least Squares)를 사용
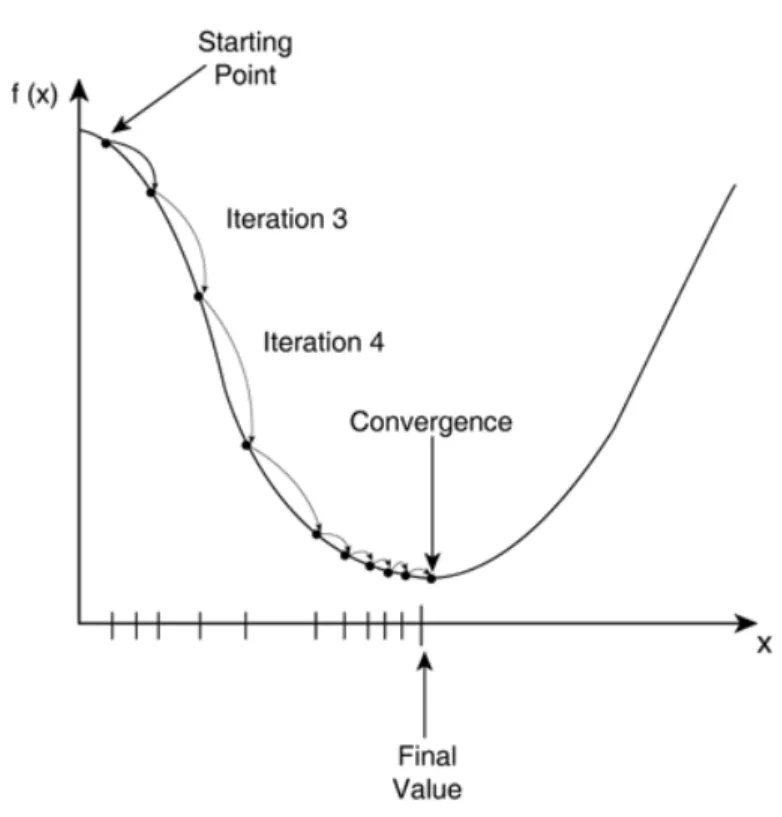
    • 경사하강법
      • 경험적으로 오차를 최소화 하는 계수를 찾아냄
      • sklearn으로 경사하강법을 사용하고 싶으면 SGDRegressor를 사용하면 됨
        (SGD는 경사하강법중 확률적경사하강법을 의미)

QnA

  • sklrean 디폴트는 수학적인 방법인가요?
    • 네
  • 학습과정이 fit() 이거 하는 거랑은 다른거죠?
    • 같은 겁니다(model.fit())
  • SGDRegressor를 특별히 사용해야 될때가 있을까요?
    • 데이터 수가 많거나 feature 수가 많을 때 수학적 계산이 복잡해지니까(선형대수 행렬 계산) 이럴 때 사용하면 좋아요
  • 경사하강법 인공신경망에서 나왔던거 같은데
    • 네~ 머신러닝에서는 다 써요!
  • 경사하강법으로 할 경우에 글로벌해 지역해(global, local) 달라서 지역해를 최종값으로 오인할 경우도 있나요(뭔가 어디서 본거같아요)
    • 네!!! 딥러닝에서 엄청 중요한 부분입니다~ 그것 때문에 최솟값에서 멈추지 않고 중간에 학습을 멈추는 경우가 있어요. 이걸 해결하기 위한 경사하강법이 따로 있어요!(머신러닝에서는 거기까지는 생각 안 하셔도 됩니다)


코드로 배우는 선형 회귀

단계별 설명

  1. 데이터 로드 및 시각화
  2. 선형 회귀 모델 학습 (scikit-learn 사용)
  3. 결과 해석
    • 학습된 직선과 데이터 비교, R2 점수 등 성능 평가

단순선형회귀 코드 예시

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 데이터 준비
X = [[1], [2], [3], [4], [5]]
y = [2, 4, 6, 8, 10]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 모델 학습
model = LinearRegression()
model.fit(X_train, y_train)

# 예측 및 평가
y_pred = model.predict(X_test)
print("MSE:", mean_squared_error(y_test, y_pred))

다중회귀 코드 예시

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split

# 데이터 생성
# 독립 변수 (x1, x2)
X = np.array([[1, 2], [2, 3], [3, 5], [4, 6], [5, 8]])
# 종속 변수 (y)
y = np.array([3, 5, 7, 9, 11])

# 학습 데이터와 테스트 데이터 분리
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 모델 학습
model = LinearRegression()
model.fit(X_train, y_train)

# 결과 확인
print("회귀 계수 (W):", model.coef_)
print("절편 (b):", model.intercept_)

# 예측
y_pred = model.predict(X_test)
print("예측 값:", y_pred)

다중회귀 with 경사하강법

from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 1. 데이터 준비
X = [[1, 2], [2, 3], [3, 5], [4, 6], [5, 8]]  # 독립 변수
y = [3, 5, 7, 9, 11]                           # 종속 변수

# 2. 데이터 분리 (훈련/테스트 데이터셋)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 3. 데이터 표준화
scaler = StandardScaler()  # SGD는 표준화된 데이터에서 더 잘 작동
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# 4. 모델 학습
sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, random_state=42, learning_rate='optimal')
sgd_reg.fit(X_train, y_train)

# 5. 예측
y_pred = sgd_reg.predict(X_test)

# 6. 평가
mse = mean_squared_error(y_test, y_pred)
print("회귀 계수 (W):", sgd_reg.coef_)  # 학습된 계수
print("절편 (b):", sgd_reg.intercept_)  # 절편
print("테스트 데이터 MSE:", mse)

QnA

  • SGDreg는 회귀분석시에만 쓰이는 거죠?
    • 네
  • 혹시 선형회귀 모델을 학습시킬때 하이퍼 파리미터를 적용하는건 어떤 방식으로 하는건가요?
    • 선형회귀에는 정할 게 없고 SGDRegressor에는 하이퍼 파라미터를 적용할 수 있는데 그냥 안 넣고 기본으로 돌리셔도 괜찮아요~
      • 선형회귀는 하이퍼 파라미터에 따른 영향이 크지 않음


회귀 모델의 확장 및 한계

선형회귀의 한계

  • 비선형 데이터에는 적합하지 않음
  • 과적합의 위험을 항상 조심해야 함
    • 과적합
      • train 데이터에서만 결과가 좋고 test 데이터에는 결과가 안 좋은 경우
      • 즉, 일반화가 안되는 경우

다양한 회귀 모델

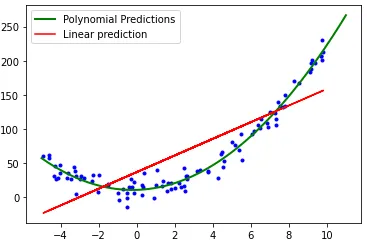
다항 회귀(Polynomial Regression)

  • 비선형 데이터를 설명할 때 사용
  • 코드
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import numpy as np

# 데이터 생성
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
y = np.array([1.5, 4.2, 9.3, 16.8, 25.1])

# 다항 특징 생성 (2차 다항식)
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)

# 모델 학습
poly_reg = LinearRegression()
poly_reg.fit(X_poly, y)

# 예측
y_pred = poly_reg.predict(X_poly)

# 결과 출력
print("다항 회귀 계수:", poly_reg.coef_)
print("절편:", poly_reg.intercept_)
print("MSE:", mean_squared_error(y, y_pred))

→ 데이터를 추가 가공해서 다항을 맞추는 것: 보면 모델은 그대로임
→ 포인트는 "다항 특징 생성(2차 다항식)"

과적합 방지용 규제(regularization)를 사용하는 회귀

  • 릿지(Ridge)
    • 수식
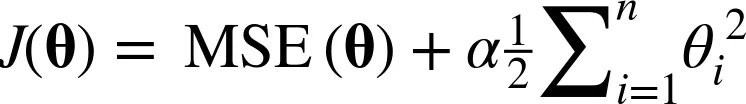
    • 코드
from sklearn.linear_model import Ridge

# 모델 학습
ridge_reg = Ridge(alpha=1.0)
ridge_reg.fit(X, y)

# 예측
y_pred = ridge_reg.predict(X)

→ alpha는 규제를 얼마나 강하게 걸 것인지 결정하는 것(0~1 사이 값)

  • 라쏘(Lasso)
    • 수식
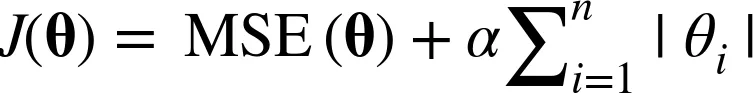
    • 코드
from sklearn.linear_model import Lasso

# 모델 학습
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)

# 예측
y_pred = lasso_reg.predict(X)
  • 엘라스틱넷(Elasticnet)
    • 수식
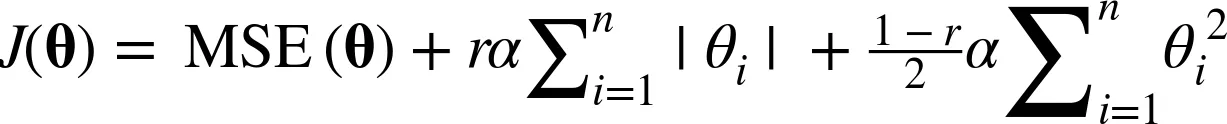
    • 코드
from sklearn.linear_model import ElasticNet

# 모델 학습
elastic_net_reg = ElasticNet(alpha=0.1, l1_ratio=0.5)  # l1_ratio=0.5: L1과 L2의 균형
elastic_net_reg.fit(X, y)

# 예측
y_pred = elastic_net_reg.predict(X)

심화 학습: 훨씬 성능 좋고 복잡한 모델을 다루고 싶다면

  • 트리기반 회귀, 딥러닝 회귀로의 확장 가능성

트리 기반 모델

  • 회귀를 수행할 때 정말 자주 사용

RandomForest

from sklearn.ensemble import RandomForestRegressor

# 모델 학습
rf_reg = RandomForestRegressor(n_estimators=100, random_state=42)
rf_reg.fit(X, y)

# 예측
y_pred = rf_reg.predict(X)

XGB

  • 별도의 패키지 설치 필수
from xgboost import XGBRegressor

# 모델 학습
xgb_reg = XGBRegressor(n_estimators=100, learning_rate=0.1, random_state=42)
xgb_reg.fit(X, y)

# 예측
y_pred = xgb_reg.predict(X)

LightGBM

  • 별도의 패키지 설치 필수
from lightgbm import LGBMRegressor

# 모델 학습
lgbm_reg = LGBMRegressor(n_estimators=100, learning_rate=0.1, random_state=42)
lgbm_reg.fit(X, y)

# 예측
y_pred = lgbm_reg.predict(X)

Catboost

  • 별도의 패키지 설치 필수
  • 가장 최근 모델(2017년)
  • 최적화가 잘 되어 있고 기능도 많아서 추천해요~
from catboost import CatBoostRegressor

# 모델 학습
catboost_reg = CatBoostRegressor(n_estimators=100, learning_rate=0.1, random_state=42)
catboost_reg.fit(X, y)

# 예측
y_pred = catboost_reg.predict(X)

딥러닝

  • CNN
  • RNN
  • LSTM
  • GRI
  • Transformer

XAI(설명가능인공지능)과의 연결

  • 최근 들어 산업계에서 단순히 결과만 잘 내고 끝내는 것이 아니라 왜 그런 결과를 냈는지 설명도 할 수 있는 것을 중요시함
  • 특히 금융, 의료, 제조 산업에서 중요!

회귀를 실제 프로젝트에서 활용한다면

  • 사용할 데이터: 캘리포니아 집값 예측

머신러닝 프로젝트 수행 과정

  1. 데이터 가져오기
    • 데이터 다운로드
    • 데이터 구조 훑어 보기
    • 테스트 데이터 만들기
      • 현업에서는 이 과정을 생략하고 실제 들어오는 데이터(실시간 데이터)로 테스트를 진행
  2. 데이터 이해를 위한 탐색과 시각화(EDA)
    • 시각화
    • 상관관계 조사
    • 특정 조합 만들어 보기
  3. 머신러닝을 위한 데이터 전처리
    • 데이터 정제
      • 결측값, 이상치 확인 등
    • 텍스트와 범주형 특성 다루기
    • 스케일링
      • 정규화, 표준화 등
  4. 모델 선택과 훈련
    • 다양한 모델들을 선택
    • 훈련 데이터로 훈련하기
  5. 모델 튜닝
    • 그리드 탐색
    • 랜덤 탐색
  6. 모델 평가하기
    • 오차분석
    • 성능평가

전체 데이터 분석과정 훑어보기



요약

  • 주요 내용 복습
    • 회귀란 무엇인가
    • 선형 회귀의 기본 원리와 실습
    • 확장된 회귀 모델과 한계
  • QnA
profile
Suhyeon Lee
2 B R 0 2 B
이전 포스트

머신러닝 특강: 분류 분석

0개의 댓글

관련 채용 정보