목표
- 회귀분석의 개념을 이해
- 회귀분석의 종류를 학습
- 회귀분성의 결과 해석 방식을 집중적으로 학습
- 데이터셋을 기반으로 회귀분석 실습
| 구분 | 상세 |
|---|---|
| 분석 기법 | 기초 통계분석 ← DONE |
| 상관분석 ← HERE! | |
| 회귀분석 ← HERE! | |
| 분류분석 | |
| 군집분석 | |
| RFM 분석 | |
| 분석 방법론 | A/B TEST ← DONE |
| 통계이론 | 기초통계이론(평균, 분산, 표준편차) ← DONE |
| 정규분포와 중심극한정리 ← DONE | |
| 신뢰구간과 유의수준 ← DONE | |
| 가설 설정 ← DONE | |
| 통계적 유의성 검정 ← DONE | |
| 통계적 가설 검정 ← DONE |
회귀분석(regression) vs. 상관분석(correlation)
회귀분석
- 회귀식을 통하여 하나 또는 둘 이상의 독립변수들을 기초로 하여 종속변수에 미치는 영향력의 크기를 알아보는 분석기법
- 회귀식에 포함된 독립변수들 중 예측력이 높은 변수의 설정이 가능
- 독립변수와 종속변수 간 가지고 있는 관련성 여부를 파악하는 데 이용
- 독립변수들 간의 상관관계가 높으면 그 변수만의 효과를 알아내기가 어렵기 때문에 특정 변수의 유의성이 상실될 수 있으므로 독립변수들 간의 상관관계가 없어야 함
- 단순회귀분석
- 독립변수가 1개
- 다중회귀분석
- 독립변수가 2개 이상
- cf. 다항회귀분석
- 별도의 알고리즘이 있는 것이 아니라 독립변수를 제곱, 서로 곱한 값 등 좀 더 복잡한 값으로 만들어 선형회귀에 넣어 학습시키는 것
- 회귀 모델식을 다차원 다항식으로 두고 회귀 분석을 수행하는 것
- 다항 회귀도 결국 다중 회귀식의 일종(자항 회귀 모델은 다중 회귀 모델로 계산될 수 있다)
- cf. 로지스틱회귀분석
- 독립 변수의 선형 결합을 이용하여 사건의 발생 가능성을 예측하는 데 사용되는 통계 기법
- 로지스틱 함수 또는 로짓 함수를 x와 y 사이의 방정식으로 사용하는 통계 모델
- 로짓 함수는 y를 x의 시그모이드 함수로 매핑
회귀모형 선택방법
- 후진제거법(backword estimation)
- 모든 독립변수를 사용해 하나의 회귀방정식을 수립하여 회귀식에 유의적으로 기여하지 못하는 독립변수 값 검정을 실시한 뒤, 그 값이 가장 작은 변수부터 하나씩 제거하고 남은 나머지 독립변수를 이용해 회귀모형을 재추정
- 전진선택법(forward selection)
- 종속변수에 가장 큰 상관관계가 있는 하나의 예측변수를 이용하여 회귀방정식을 수립한 뒤, 연구자의 기준에 의거하여 각 단계마다 독립변수를 하나하나씩 회귀식에 포함시켜 회귀방정식을 다시 계산하여 새로운 독립변수의 부분 검정을 통해 기여도를 계산
- 단계별 선택법(stepwise selection)
- 전진선택법과 후진제거법의 절충적인 형태
- 전진선택법에 의해 종속변수에 가장 큰 상관관계가 있는 독립변수를 택하는 동시에 각 단계에서 후진제거법과 같이 회귀식에 유의적으로 기여하지 못하는 독립변수를 제거하는 방법
- 가장 많이 사용되는 방법임
상관분석
- 변수들 간의 상호관계 정도를 분석하는 통계적 기법
- 하나의 변수와 다른 변수와의 어떤 밀접한 관련성을 갖고 변화하는가를 분석
- cf. 회귀분석은 하나의 변수가 나머지 다른 변수들과의 선형적 관계를 갖는가의 여부를 분석
- 변수들 간의 관련성의 정도는 특정 변수의 분산 중에 다른 변수와 같이 변화하는 분산, 즉 공분산이 어느 정도 되느냐에 따라 좌우됨
단순상관관계분석
- 두 변수 간의 관계 정도를 밝히는 것
다중상관관계분석
- 셋 또는 그 이상의 변수들 간의 상호관계 정도를 밝히는 것
공분산
- 공분산이 많을수록 상관도가 높게 나타나고, 공분산이 완전히 일치하면 상관관계는 1이 됨
상관계수
- 상관관계의 정도를 나타내 주는 것
- 정규분포된 양적 변수에 대해서는 Pearson 상관계수를 사용
- 정규적으로 분포되어 있지 않거나 범주 순서가 지정되어 있지 않을 때는 순서 간 관계를 측정하는 Kendall Tau-b()나 Spearman을 이용
- 변수 값의 평균과 분산을 사용하는 피어슨 상관 계수는 변수 값이 정규분포를 따르지 않으면 잘못된 결과를 얻을 수 있음 → 켄달타우(kendalltau)는 이러한 단점을 보안해 주며 두 변수들 간의 순위를 비교하여 연관성을 계산함
- 상관계수 범위는 -1(완전 음의 관계)부터 +1(완전 양의 관계)까지이며 0은 선형 관계가 아님을 나타냄
부분상관계수
- 상관관관계분석 기법 중 하나
- 다른 변수들과 같이 변화하는 부분을 제거시킨 뒤 순수하게 두 변수간의 상관관계만 특정하는 것
cf. 정준상관분석(Cannonical Correction)
- 2개 이상의 변수로 구성되어 있는 종속 변수와 2개 이상으로 구성되어 있는 독립 변수 간의 관계를 살펴보는 기법
- 종속 변수군과 독립 변수군들 사이의 관계를 상관관계분석과 회귀분석 등을 이용하여 분석하는 기법
- 상관관계분석은 각 변수들 간의 상관관계를 구하는 반면 정준상관관계분석은 종속변수과 독립변수들의 선형식을 각각 구하고 이것을 가지고 상관관계를 구하는 기법
- 회귀분석은 하나의 종속변수와 한 개 이상의 독립변수들을 가지고 회귀식을 도출하여 종속변수와 독립변수의 관계를 살펴보는 반면 정준상관관계분석은 다수의 종속변수와 다수의 독립변수들을 이용하여 선형의 식을 도출하는 점에서 차이가 있음
상관관계와 회귀분석은 모두 두 변수 간의 관계를 이해하는 데 사용되는 통계 방법
하지만 목적, 분석 대상, 결과 해석 등에서 차이가 있음
1. 분석 목적
- 상관관계분석
- 두 변수 간 관계의 강도와 방향성 파악
- 두 변수 간 관계를 이해하고 예측
- 회귀분석
- 독립변수와 종속변수 사이의 함수적 관계를 분석하고 이를 이용하여 종속변수를 예측하는 모델 생성
- 분석 대상
- 상관관계분석
- 두 변수 간의 상관성(관련성) 분석에 중점
- 두 변수 간의 관계를 파악할 때 적용
- 회귀분석
- 독립변수와 종속변수 간의 인과관계 분석
- 종속변수에 영향을 미치는 독립변수를 파악
- 독립변수의 값을 이용하여 종속변수 예측하는 모델 생성
- 결과 해석
- 상관관계분석
- 상관계수를 이용하여 두 변수 간 관계 파악
- 상관계수: -1부터 1까지의 값
- 절댓값이 1에 가까울수록 강한 상관관계
- 부호는 상관관계의 방향성
- 회귀분석
- 회귀식과 회귀계수 등을 이용
- 회귀계수: 독립변수의 영향 정도와 방향성
- 독립변수와 종속변수 간 관계를 이해하고 독립변수의 값이 종속변수에 미치는 영향을 파악하여 예측하는 모델을 생성하기 때문
-
사용 목적
- 상관관계분석
- 두 변수 간의 관계를 이해하고 예측
- 회귀분석
- 종속변수에 영향을 미치는 독립변수의 효과를 분석하여 예측
- 상관관계분석
-
사용 가능한 변수 개수
- 상관관계분석
- 2개의 변수만 사용
- 회귀분석
- 단순회귀분석: 독립변수 1개 종속변수 1개
- 다중회귀분석: 임의의 수
- 상관관계분석
-
결과
- 상관관계분석
- 상관계수(-1에서 +1까지)
- 회귀분석
- 회귀방정식(y=a+bx)
- 상관관계분석
-
인과 관계 식별
- 상관관계분석
- X
- 회귀분석
- O
- 상관관계분석
회귀분석이란?
회귀분석 이해하기
- 게임시간과 전기세에 대한 데이터
| 게임 시간 | 전기세 |
|---|---|
| 2시간 | 500원 |
| 4시간 | 1130원 |
| 10시간 | 2740원 |
| … | … |
→ 이를 그래프로 그리면 아래와 같은 형태를 가짐
- x축은 게임시간, y축은 전기세를 의미
- 점들은 각 데이터를 의미
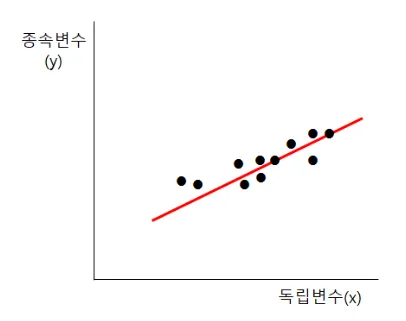
독립변수: 원인이 되는 변수 → 게임시간
종속변수: 결과가 되는 변수 → 전기세
- 게임 시간이 1000시간이면, 전기세는 얼마일까?
- 우리가 가진 데이터셋에 해당 값이 없을 때 이를 '예측'(추정)하기 위해 "회귀분석"의 개념을 도입
- 예측을 위해 위 그래프에서 붉은색으로 보이는 '추세선'이 필요
🡆 회귀분석의 목적 == '추세선'을 찾는 것
추세선
- "우리가 이미 가지고 있는 데이터들을 가장 잘 설명해주는 선"을 의미
- (방정식)으로 표현
- : 게임 시간(독립변수)
- : 전기세(종속변수)
- : 절편(x가 0일 때 y값)
- : 기울기
- 추세선을 파악함으로써, 게임 시간이 1000시간일 때 추세선과 만나는 점을 통해 종속변수를 예측할 수 있음
- 이러한 특징을 통해 데이터 분석에서는 예측을 진행할 때 회귀분석을 주로 수행
회귀분석 요약
- 역사
- 통계학에서 '회귀'라는 용어는 1889년 프란시스 갈튼경(Sir Francis Galton)이 특정 현상을 설명하기 위해 '평균으로의 회귀'라는 용어를 사용하면서 시작되었습니다.
- 특정 현상: 유전에 의하여 보통사람의 신장으로 회귀(Regression toward Meiocrity in Hereditary Stature) → 부모와 자녀의 키가 어떠한 관계를 갖는지 분석: 부모의 키가 크(작)더라도 그 자식들은 결국 보통 키로 회귀하려는(돌아가려는) 경향이 있음
- 통계학에서 '회귀'라는 용어는 1889년 프란시스 갈튼경(Sir Francis Galton)이 특정 현상을 설명하기 위해 '평균으로의 회귀'라는 용어를 사용하면서 시작되었습니다.
- 정의
- 독립변수(x)로 종속변수(y)를 예측하는 분석기법
- 독립변수: 원인이 되는 변수로, 설명변수라고도 불립니다.
- 종속변수: 결과가 되는 변수로, 반응변수라고도 불립니다.
- 독립변수(x)로 종속변수(y)를 예측하는 분석기법
- 프로세스
- 일반적으로 3단계를 통해 분석 진행
- 독립변수, 종속변수 설정
- 독립변수와 종속변수를 정하고 가설을 설정
→ 독립변수: 게임시간
→ 종속변수: 전기세
→ 귀무가설:
게임시간은 전기세와 관련이 없을 것이다.
→ 대립가설:
게임시간은 전기세와 관련이 있을 것이다.
- 독립변수와 종속변수를 정하고 가설을 설정
- 데이터 경향성 확인
- 독립변수와 종속변수 간 산점도 분석 및 상관관계 분석을 통해 데이터 분포를 확인
🡆 원인과 결과에 대한 인과분석이 아니라 '관련이 있는가 없는가'에 대한 '상관분석'!
- 독립변수와 종속변수 간 산점도 분석 및 상관관계 분석을 통해 데이터 분포를 확인
- 정합성 검증 & 결과 해석
- 회귀분석 결과를 해석하기 위해 다음 3가지 살펴보기
① 회귀모델(회귀식)이 얼마나 설명력을 갖는지 →
② 회귀모델(회귀식)이 통계적으로 유의한지
③ 독립변수와 종속변수 간 선형관계가 있는지
- 회귀분석 결과를 해석하기 위해 다음 3가지 살펴보기
🡆 A/B 테스트와 전체적인 흐름이 비슷합니다~
귀무/대립가설 설정(실험하려면 명제가 있어야 하니까) → 데이터 경향성 확인 → 유의성(유의수준) 설정 → 실험하고 해석
회귀분석의 특징, 종류
- 주요한 특징들을 장점과 단점으로 나누어 살펴보기
- 다양한 종류 중 데이터 분석에서 가장 많이 사용되는 유형 살펴보기
특징
- 장점
- 친밀성
- 예측문제 해결에서 가장 많이 사용되고 있는 방법
- 분석 및 해석 방법이 다수 존재
- 유용성
- 결과에 대한 근거, 이유, 활용방안 등의 정보를 얻는 데 유용
- 유연성
- 종속변수를 설명하기 위한 다양한 독립변수를 선택하고 실험할 수 있음
- 친밀성
- 단점
- 복잡성
- 기본 가정이 어긋나면 회귀분석을 사용할 수 없음
- 한계성
- 비선형성 확인을 위한 적절한 방식이 존재하지 않음
- 복잡성
종류
- 회귀 계수의 선형여부, 독립변수의 개수, 종속변수의 개수에 따라 여러 가지 유형으로 나눌 수 있음
선형회귀분석
- 독립변수
- 연속형
- 종속변수
- 연속형
- 분석 목적
- 예측
- 분석 방법
- 선형방정식에 의한 함수식 표현
- 종류
- 단순 회귀
- 단순회귀는 독립변수 1개, 종속변수 1개인 경우
- 방정식:
- : 예측된 회귀선
- : y절편
- : 회귀 계수(slope, 기울기) → 설명변수 X의 변화에 따라 반응변수 y가 반응하는 정도
- 다중 회귀
- 다중회귀는 독립변수가 2개 이상이고, 종속변수가 1개인 경우
- 방정식:
- 예시
- 공부 시간(독립변수)에 따른 시험 점수(종속변수)
→ 단순 회귀 - 치킨 판매량(독립변수)에 따른 맥주 판매량(종속변수)
→ 단순 회귀 - 주택의 면적(독립변수), 방 개수(독립변수), 욕실 개수(독립변수)에 따른 주택 가격(종속변수)
→ 다중 회귀
- 공부 시간(독립변수)에 따른 시험 점수(종속변수)
로지스틱회귀분석
- 독립변수
- 연속형
- 범주형
- 종속변수
- 범주형이면서 이진형(예/아니오, 0/1, 앞/뒤)
- 순서가 없는 범주형(시험등급/과일분류/고객만족도)
- 분석 목적
- 분류
- 예측
- 분석 방법
- 연결함수를 이용한 함수식 표현
- 종류
- 이진 로지스틱 회귀
- 종속변수가 두 가지 중 하나의 값을 가지는 경우
- 다중 로지스틱 회귀
- 종속변수가 순서가 없는 3개이상일 경우
- 이진 로지스틱 회귀
- 예시
- 공부시간(독립변수)에 따른 시험합격여부(종속변수)
→ 이진 로지스틱 회귀 - 서비스 응답시간(독립변수)에 따른 고객만족도(종속변수)
→ 다중 로지스틱 회귀
- 공부시간(독립변수)에 따른 시험합격여부(종속변수)
🡆 현업에서는 분석한 결과를 가지고 모델링을 함
즉, 이 프로세스를 모델에 올린다는 이야기 → 데이터가 들어올 때마다 파이썬 코드를 돌리는 건 비효율적이니까!
계산한 결과를 가지고 모델에 저장해 다음에 데이터가 들어왔을 때 모델만 불러와서 모델을 돌렸을 때 똑같은 결과를 낼 수 있도록 함(저장해놓고 불러오기) → 모델 정확도를 보는 이유!
정합성 검증 & 결과 해석
- 선형회귀분석 결과 해석하는 법
결정계수 확인: 회귀모델(회귀식)이 얼마나 설명력을 갖는가?
-
결정계수(; R_squared)
- 종속변수와 독립변수의 관계를 나타내는 수치
-
결정계수 해석을 위해 회귀식이 도출되는 과정을 확인해 보기
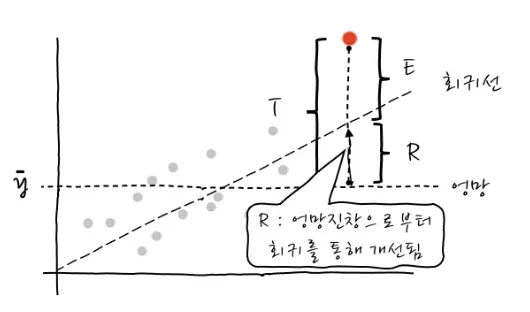
- 기울기가 0, y절편이 y의 평균인 선을 통해, 엉망인 회귀선을 그릴 수 있습니다.(그림에서 점선&엉망이라고 표시된 부분)
- 여기에 T, R, E 개념을 더합니다.
- T = Total: 전체 변동
- R = Regresssion:
회귀분석을 통해서 찾아낸 회귀선까지의 변동
※ 여기서의 R은 설명력(R²)과 다릅니다!
- E = Error: 잔차(회귀로 설명할 수 없는 여전히 존재하는 변동) - 설명력()은 전체 오류 중 회귀를 함으로써 얼마나 개선되었는가를 의미
- 0과 1 사이의 값을 가지며, 1에 가까울수록 모델의 성능이 좋다는 것을 의미
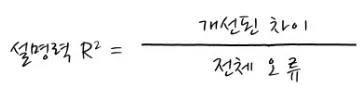
- 0과 1 사이의 값을 가지며, 1에 가까울수록 모델의 성능이 좋다는 것을 의미
🡆 엉망진창인 상태에서 회귀식을 통해 원래 위치에 얼마나 가까워졌는지로 설명력 지표를 삼음
F검정: 회귀모델(회귀식)이 통계적으로 유의한가?
- 회귀식에 대한 F검정 시행
🡆
결정계수: 전체 오류 중에서 얼마나 보완할 수 있는가?
F검정: 보완할 수 있다는 건 알았는데 그래서 이거 써도 되나요?
| 가설 | 명제 |
|---|---|
| 귀무가설 | 회귀모델은 타당하지 않을 것이다. |
| = 회귀 계수들이 모두 0이다. | |
| 대립가설 | 회귀모델은 타탕할 것이다. |
| = 적어도 하나의 회귀 계수는 0이 아니다. |
- p-value로 유의성 판단
- p-value 는 ‘신뢰도’에 대한 검정통계량
- F-검정을 통해 얻은 p-value 값이 0.05보다 작다면 대립가설을 채택합니다. (신뢰도95%)
(기울기)에 대한 t 검정: 독립변수와 종속변수 간 선형관계가 있는가?
| 가설 | 명제 |
|---|---|
| 귀무가설 | 독립변수와 종속변수 간 선형적인 연관이 없을 것이다. |
| 대립가설 | 독립변수와 종속변수 간 선형적인 연관이 있을 것이다. |
- p-value로 유의성 판단
- t-검정을 통해 얻은 p-value 값이 0.05보다 작다면 대립가설을 채택합니다.
OLS(Ordinary Least Squares) 해석
- OLS는 선형 회귀 모델의 결과를 나타내는 회귀 결과 표
- OLS가 지원하는
summary함수를 통해 아래와 같은 결과표를 얻을 수 있음
- OLS가 지원하는
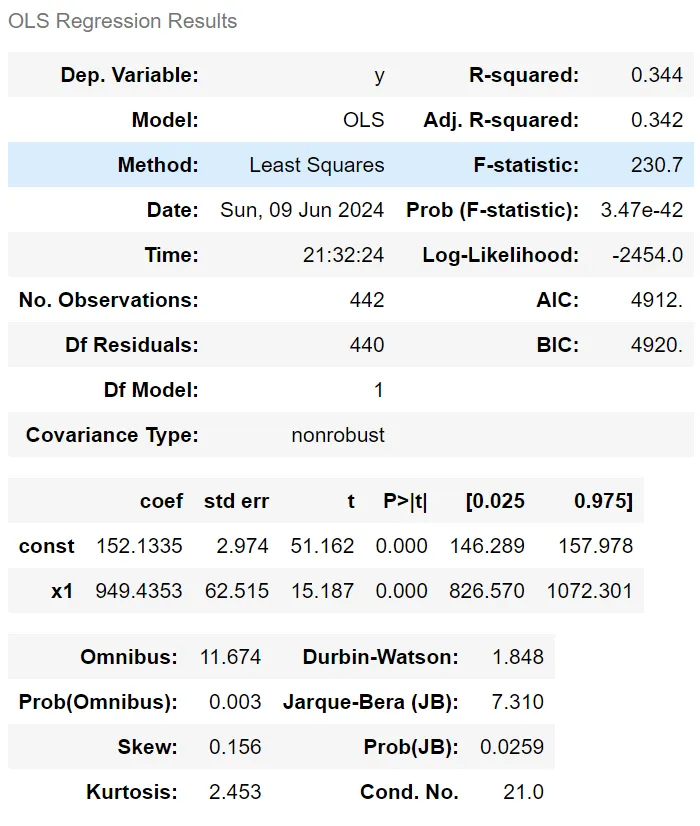
- 지표 해석
- Dep. Variable (y): 종속 변수, 즉 회귀분석에서 설명하고자 하는 변수입니다.
- R-squared (0.344): 결정계수로, 회귀 모델이 종속 변수의 변동성을 얼마나 설명하는지를 나타냅니다. 이 값은 0에서 1 사이에 위치하며, 0.344는 약 34.4%의 변동성이 설명된다는 것을 의미합니다.
- Adj. R-squared (0.342): 수정된 결정계수로, 설명 변수의 개수를 고려하여 R-squared 값을 조정한 것입니다. 변수의 수가 늘어날 때 발생하는 과적합을 방지하기 위해 사용됩니다. 0.342는 모델이 적절하게 조정되었음을 나타냅니다.
- Method (Least Squares): 사용된 회귀 방법이 최소제곱법임을 나타냅니다.
- 최소제곱법: 근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합이 최소가 되는 해를 구하는 방법
- F-statistic (230.7): 회귀 모형의 전체 유의성을 검정하는 F-통계량입니다. 값이 클수록 모형이 유의미할 가능성이 높습니다.
- Prob (F-statistic) (3.47e-42): F-통계량의 p-값으로, 이 값이 매우 작으면 (예: 0.05 이하) 대립가설을 채택할 수 있습니다. 이 경우 p-값이 거의 0에 가까우므로, 회귀 모형이 통계적으로 유의미하다고 볼 수 있습니다.
- Log-Likelihood (-2454.0): 회귀 모형의 로그 우도(likelihood)입니다. 값이 클수록 모형이 데이터에 더 잘 맞는다는 것을 의미합니다.
- No. Observations (442): 사용된 관측치(데이터 포인트)의 수입니다.
- Df Residuals (440): 잔차의 자유도, 즉 전체 데이터 포인트 수에서 회귀 계수의 수를 뺀 값입니다.
- Df Model (1): 모델에 포함된 설명 변수의 수입니다.
- Covariance Type (nonrobust): 공분산 추정의 유형을 나타냅니다.
nonrobust는 기본 공분산 추정이 사용되었음을 의미합니다. - coef (coefficients):
- const (152.1335): 상수항(절편)으로, 독립변수가 0일 때 종속 변수의 예측값입니다.
- x1 (949.4353): 설명 변수 x1의 회귀 계수로, 독립변수가 1 단위 증가할 때 종속 변수가 평균적으로 949.4353 단위 증가한다는 의미입니다.
- std err (Standard Error): 회귀 계수 추정치의 표준 오차입니다. 상수항과 x1에 각각 2.974, 62.515가 있습니다.
- t (t-statistic): 회귀 계수가 0인지 검정하는 t-값입니다. 절대값이 클수록 해당 계수가 유의미할 가능성이 높습니다. x1의 t-값은 15.187로 매우 크며 유의미함을 나타냅니다.
- P>|t| (P-value): 각 계수에 대한 p-값입니다. 일반적으로 0.05보다 작으면 해당 계수는 유의미하다고 판단됩니다. x1과 상수항의 p-값은 모두 0으로, 매우 유의미합니다.
- [0.025 0.975] (Confidence Interval): 회귀 계수에 대한 95% 신뢰구간입니다. 예를 들어, x1의 신뢰구간은 [826.570, 1072.301]로, 이 범위 내에서 실제 계수가 있을 가능성이 95%입니다.
- Omnibus (11.674): 잔차의 정규성을 검정하는 Omnibus 검정 통계량입니다. 값이 작을수록 잔차가 정규분포에 가깝다는 의미입니다.
- Prob(Omnibus) (0.003): Omnibus 검정의 p-값입니다. 0.05보다 작으므로 잔차가 정규분포에서 벗어날 가능성이 있습니다.
- Skew (0.156): 잔차의 왜도(skewness)입니다. 값이 0에 가까울수록 대칭적입니다.
- Kurtosis (2.453): 잔차의 첨도(kurtosis)입니다. 3에 가까울수록 정규분포에 가깝습니다. 2.453은 정규분포보다 조금 더 평평함을 의미합니다.
- Durbin-Watson (1.848): 잔차의 자기상관을 검정하는 통계량입니다. 2에 가까우면 자기상관이 없음을 의미합니다.
- Jarque-Bera (JB) (7.310): 잔차의 정규성을 검정하는 Jarque-Bera 검정 통계량입니다.
- Prob(JB) (0.0259): Jarque-Bera 검정의 p-값입니다. 0.05보다 작아 잔차가 정규성을 만족하지 않을 가능성이 있습니다.
- Cond. No. (21.0): 설명 변수의 다중공선성을 나타내는 조건수입니다. 값이 높으면 다중공선성 문제가 있음을 시사합니다.
요약
- 회귀분석
- 독립변수와 종속변수가 나누어진(또는 나눌 수 있는)데이터를 기반으로 진행
- 독립변수는 원인, 종속변수는 결과
- 독립변수와 종속변수가 나누어진(또는 나눌 수 있는)데이터를 기반으로 진행
- 귀무가설과 대립가설의 의미
- 귀무가설은 차이가 없거나 의미 있는 차이가 없는 경우의 가설
- 대립가설은 차이가 있는 경우의 가설
- 회귀분석은 크게 3단계로 진행
- 독립변수, 종속변수 설정
- 데이터 경향성 확인
- 정합성 검증 & 결과 해석
- 회귀분석의 결과해석을 위해, 세 가지 검증이 필요
- 회귀식이 얼마나 설명력을 가지는지
→ - 회귀식이 통계적으로 유의한지
→ F검정 - 독립변수와 종속변수 간 상관관계가 유의미한지
→ 기울기에 대한 t검정
- 회귀식이 얼마나 설명력을 가지는지
- 각각의 검정통계량(t-value, F-value)이 가지는 숫자의 의미보다, 이를 신뢰할 수 있는지(p-value)에 포커스 맞추기
