[NLP] 차근차근 트랜스포머 수식 이해하기 (작성중)

ㄴ 얘보다 멋있음

Intro

트랜스포머를 이해하기 위해 몸부림 치던 중, 어느 현자의 포스트를 발견했다.
Solving Transformer by Hand: A Step-by-Step Math Example

이 글은 위 포스트를 번역, 오류 정정, 요약하여 재구성한 글이다.
원글에 오류가 많아 나름 수정해봤는데, 틀린 부분이 있다면 지적해주길 바란다.
정확한 값에 집중하기보다는 전체적인 흐름을 파악하는 것이 좋을 것 같다.

---

Encoder Part

Step 1 - 데이터셋 정의

• ChatGPT에 사용된 데이터셋은 무려 570GB ..!
• 하지만 이 글에서 사용할 데이터셋은 오직 세 문장이다.
  

Step 2 - Vocab

• Vocab = 데이터셋 내 고유한 단어들의 집합
  
• Vocab Size = 데이터셋 내 고유한 단어의 수
• Vocab Size는 다음 과정을 통해 구할 수 있다.
  

  1. 각 문장을 단어 단위로 쪼개어 전체 단어 수를 구한다. (N)
  2. 중복된 단어를 제거한다. (set)
  3. 중복이 제거된 단어의 수를 센다. (count)

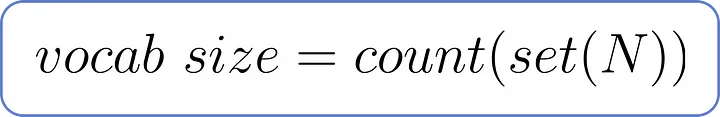
• 정리하자면, 위의 수식으로 Vocab Size를 구할 수 있다.
• 이 데이터셋의 Vocab Size는 23이다. 즉, 데이터셋에는 23개의 고유한 단어가 존재한다.

Step 3 - Encoding

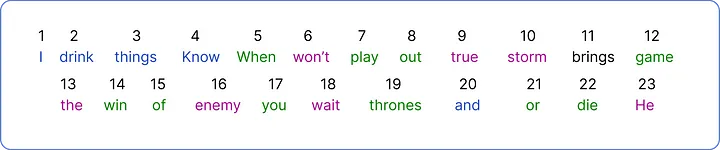
• 앞서 구한 Vocab의 고유한 단어마다 고유한 숫자를 할당해보자.
  

Step 4 - Input Embedding

• Vocab의 단어를 조합해, "When you play game of thrones" 라는 문장을 트랜스포머에 입력해보자. (왕죄의 게임 명대사인 것 같다.)

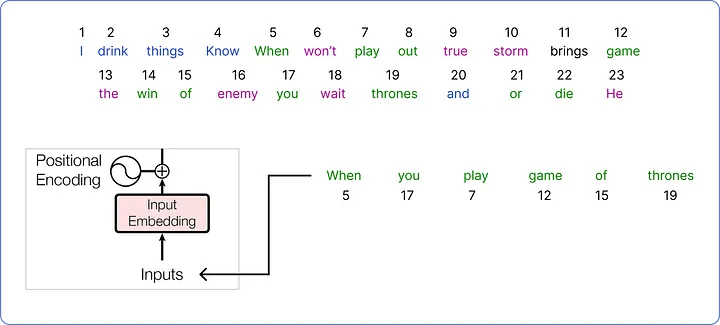
• 이제 이 입력 문장의 입력 임베딩(Input Embedding)을 구해야 한다.

• 논문(Attention is All You Need)에서는 각 입력 단어를 512차원의 임베딩 벡터로 나타내었으나,
  
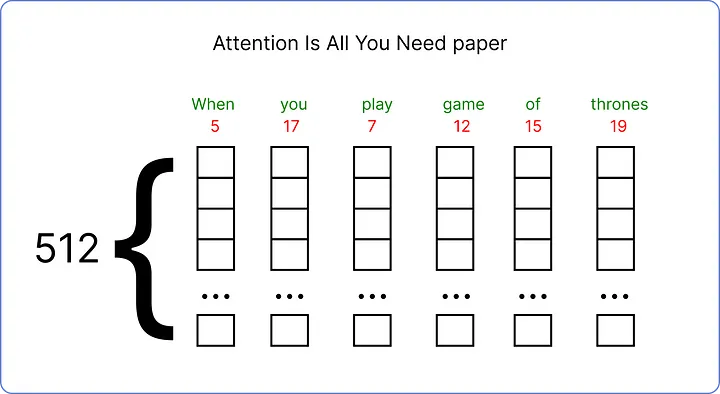
• 이 예제에서는 계산 과정을 시각화하기 위해 6차원의 임베딩 벡터를 사용하겠다.
  
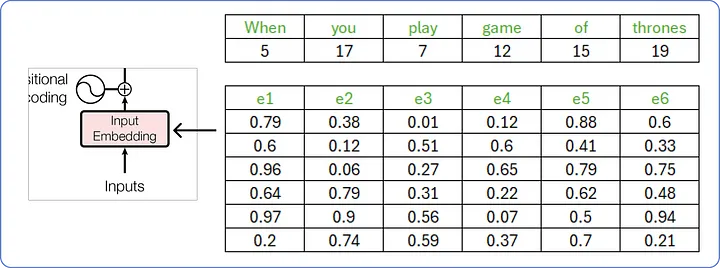
• 처음에 입력 임베딩은 0에서 1 사이의 무작위 값으로 초기화된다.
• 이 값들은 나중에 트랜스포머가 단어 사이의 의미를 이해함에 따라 업데이트된다.

Step 5 - Positional Encoding

• 이제 입력을 위한 위치 인코딩(Positional Encoding)을 구해야 한다.
• 위치 인코딩 값은 아래의 수식으로 정해진다.

$i$: 입력 임베딩 행렬의 몇 번째 행인지
$pos$: 입력 임베딩 행렬의 몇 번째 열인지
$d_{model}$: 임베딩 벡터가 몇 차원인지 (이 예제에서는 6으로 가정)

• 따라서, 첫 번째 단어인 'When'은 다음과 같은 위치 인코딩 $p1$을 갖는다.
  

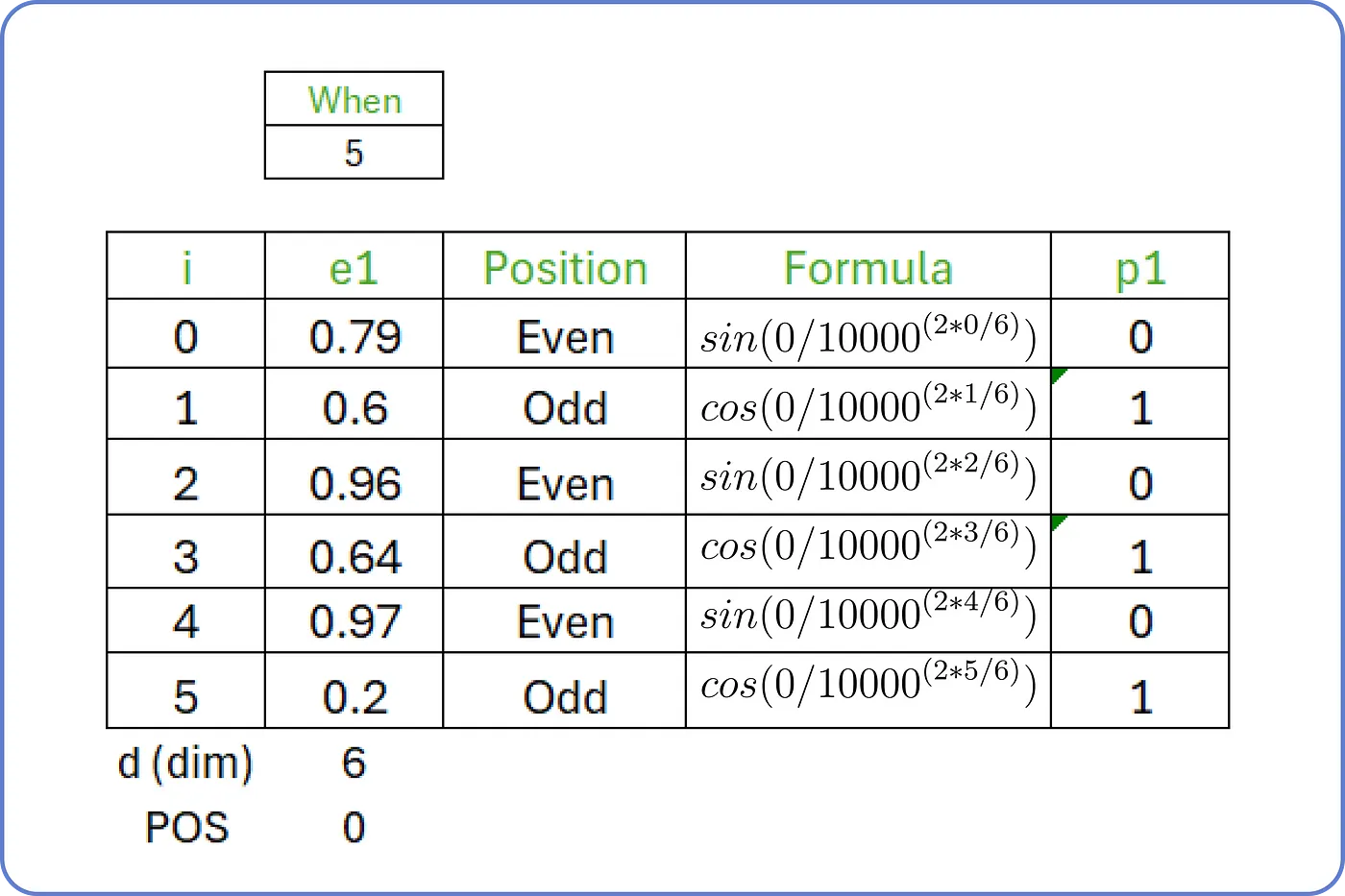
• 같은 방식으로 계산해보면, 입력 문장은 다음과 같은 위치 인코딩 $p1$~$p6$을 갖는다.
  

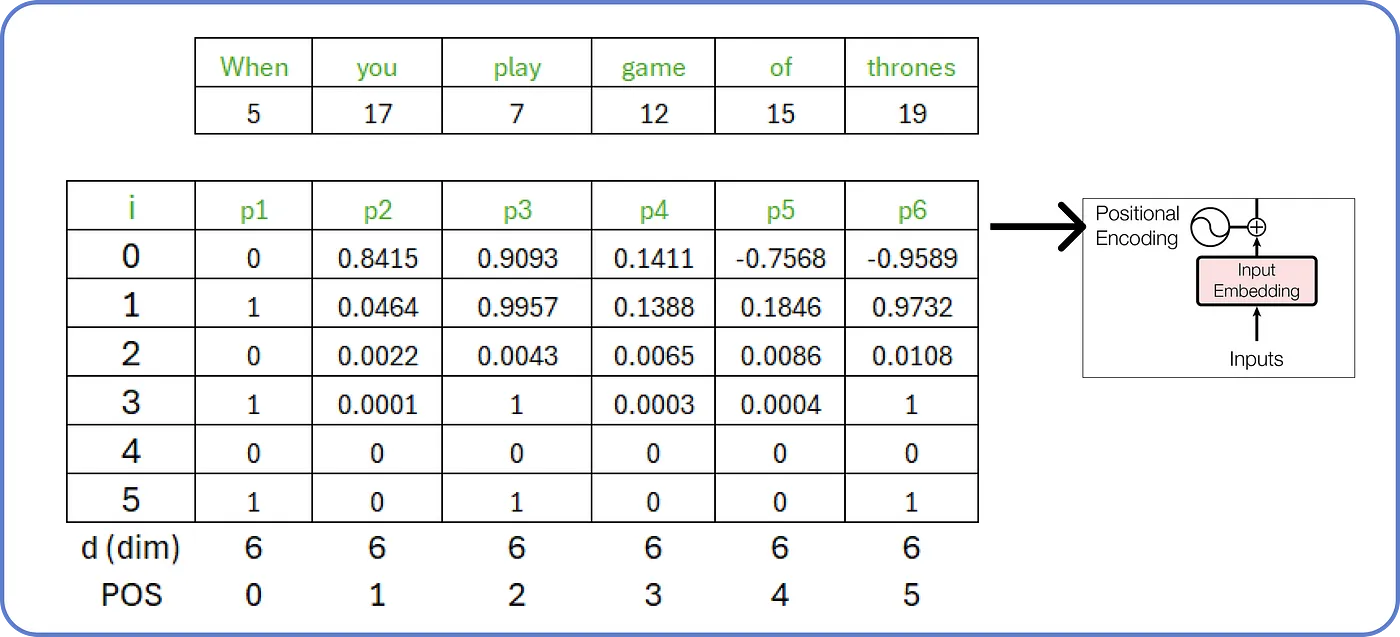
Step 6 - Input Embedding + Positional Encoding

• 이제 위에서 구한 입력 임베딩과 위치 인코딩을 더한다.
  
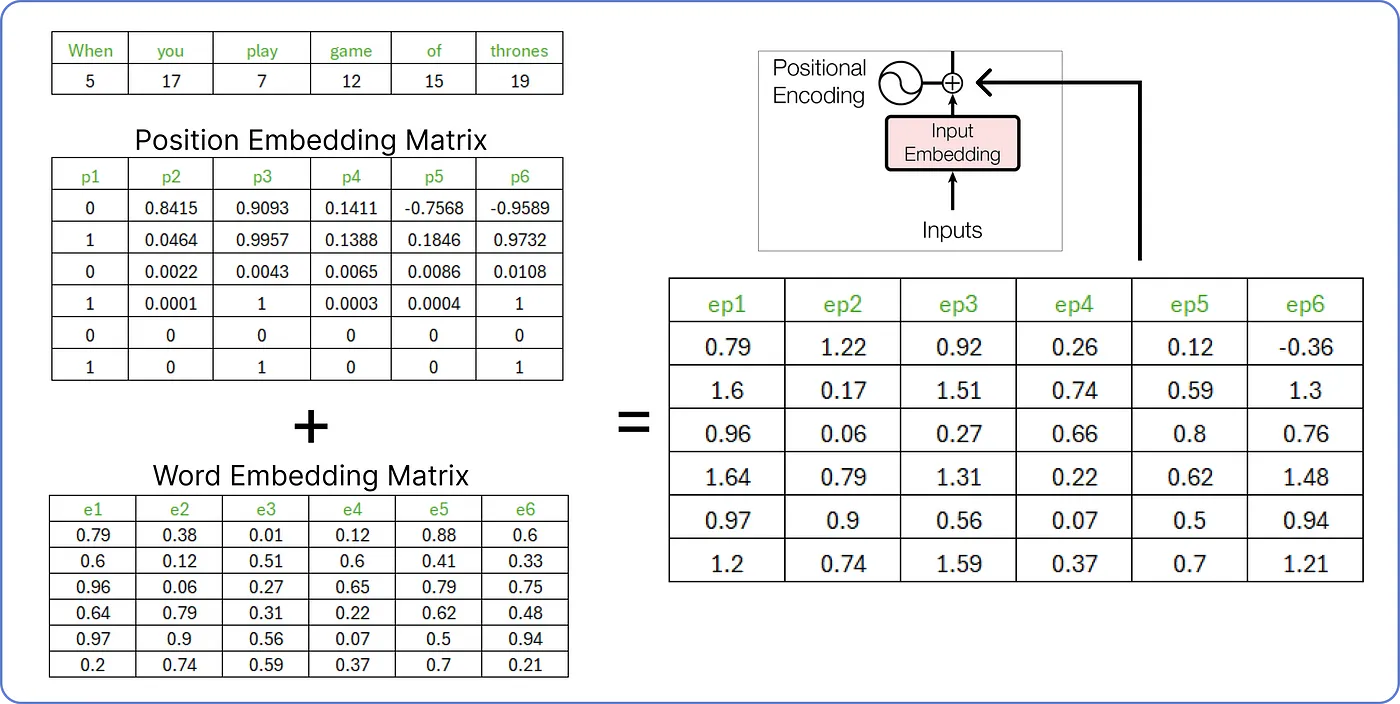
• 결과로 나온 행렬은 인코더의 입력이 된다. (이하 X 행렬이라고 칭하겠다.)

Step 7-1 - Single-Head Attention

• 트랜스포머에서는 Scaled Dot-Production Attention을 통해 Single-Head Attention을 구현한다.
  

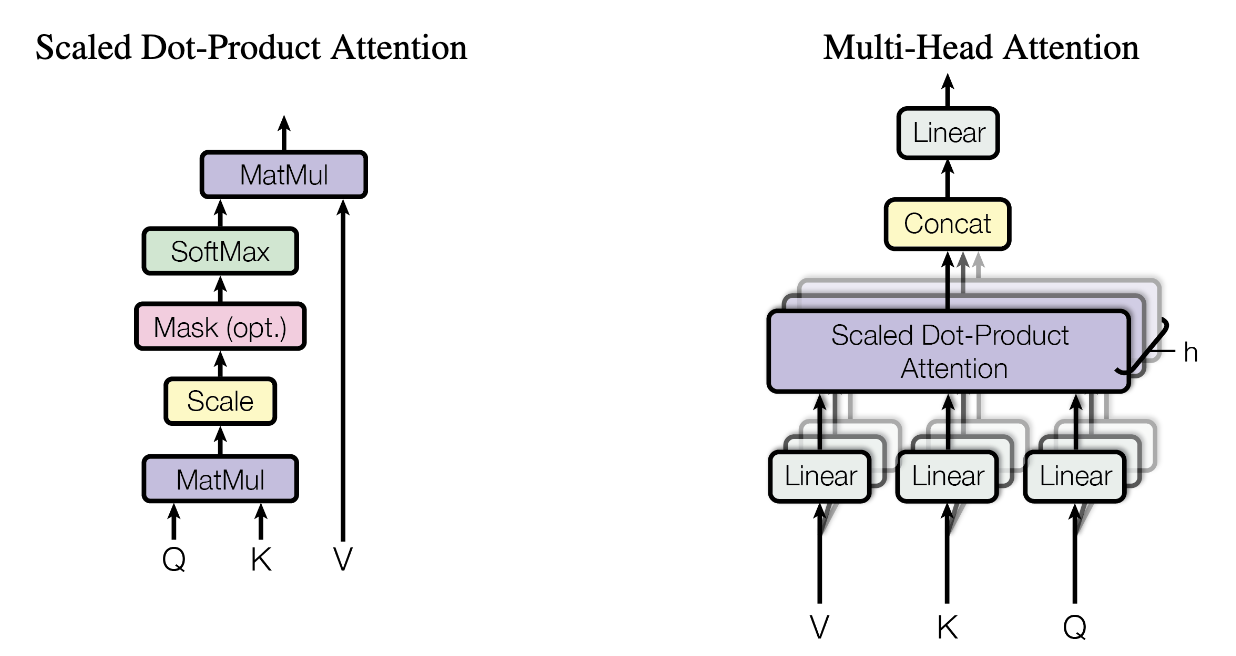
Query, Key, Value

• Single-Head Attention에는 Query, Key, Value의 세 가지 입력이 존재하는데,
  이는 인코더 입력 행렬 $X$가 선형 변환을 거침으로써,
  즉 $X^T$와 각각의 선형 가중치 행렬 $W^Q, W^K, W^V$의 곱으로 구할 수 있다.
• 인코더 입력 행렬이 선형 변환을 거치는 이유는 Query, Key, Value의 차원을 줄여 병렬 연산에 적합하게 하기 위함이다.

• 따라서 다음과 같이 Query 행렬을 구할 수 있다.
  

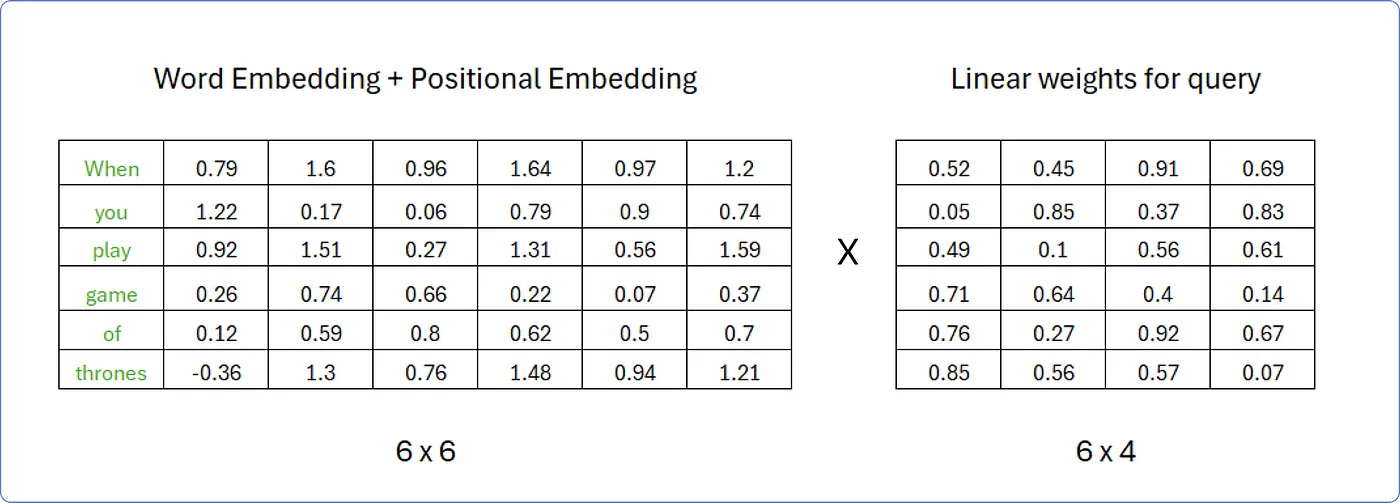
• 마찬가지로, Key와 Value 행렬도 다음과 같이 구할 수 있다.
  

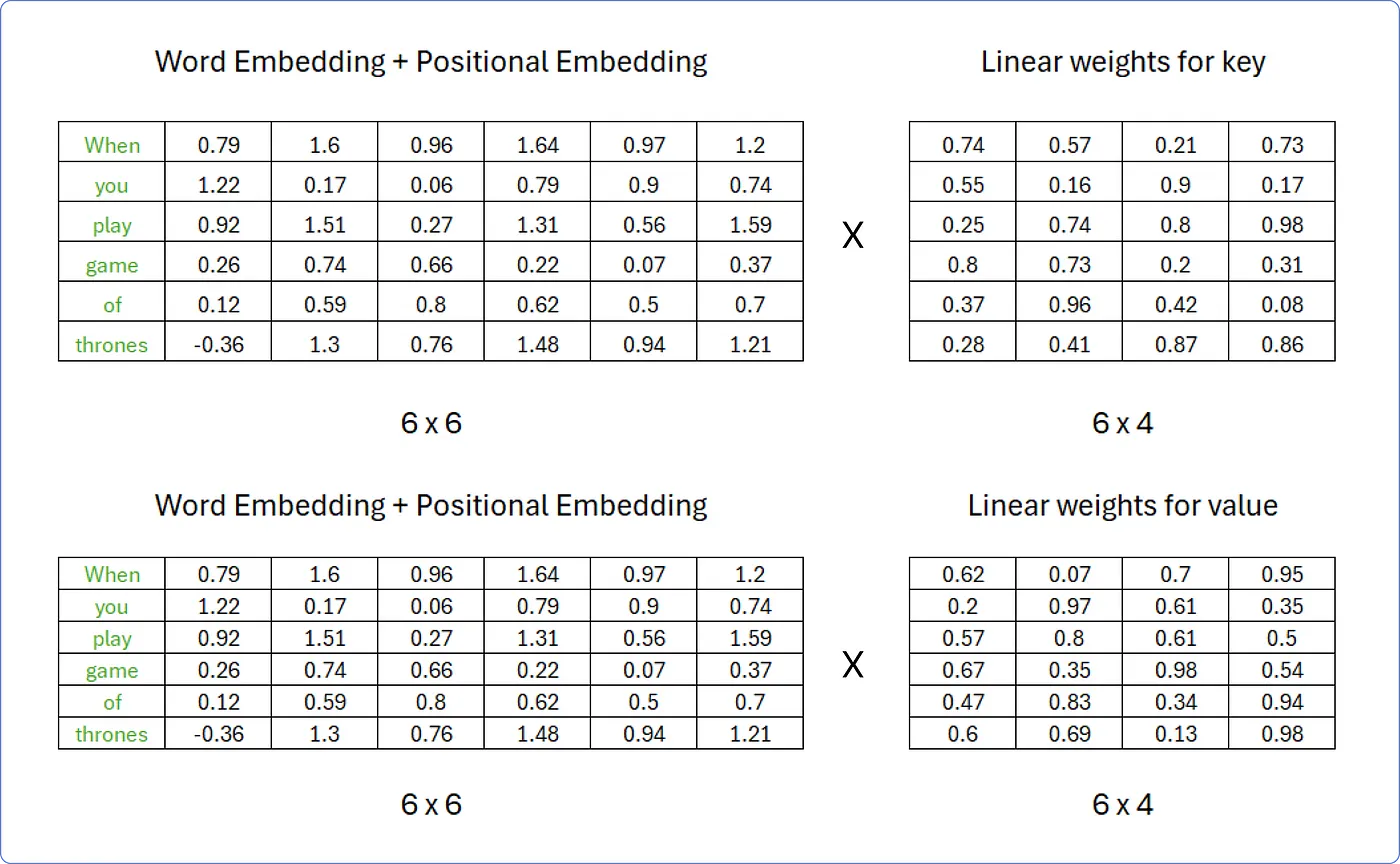
• 결과적으로, Query, Key, Value 행렬은 다음과 같다. (벡터 개수 x 차원)
  예시) 아래의 Query 행렬은 4차원의 Query 벡터 6개로 구성된다.
  

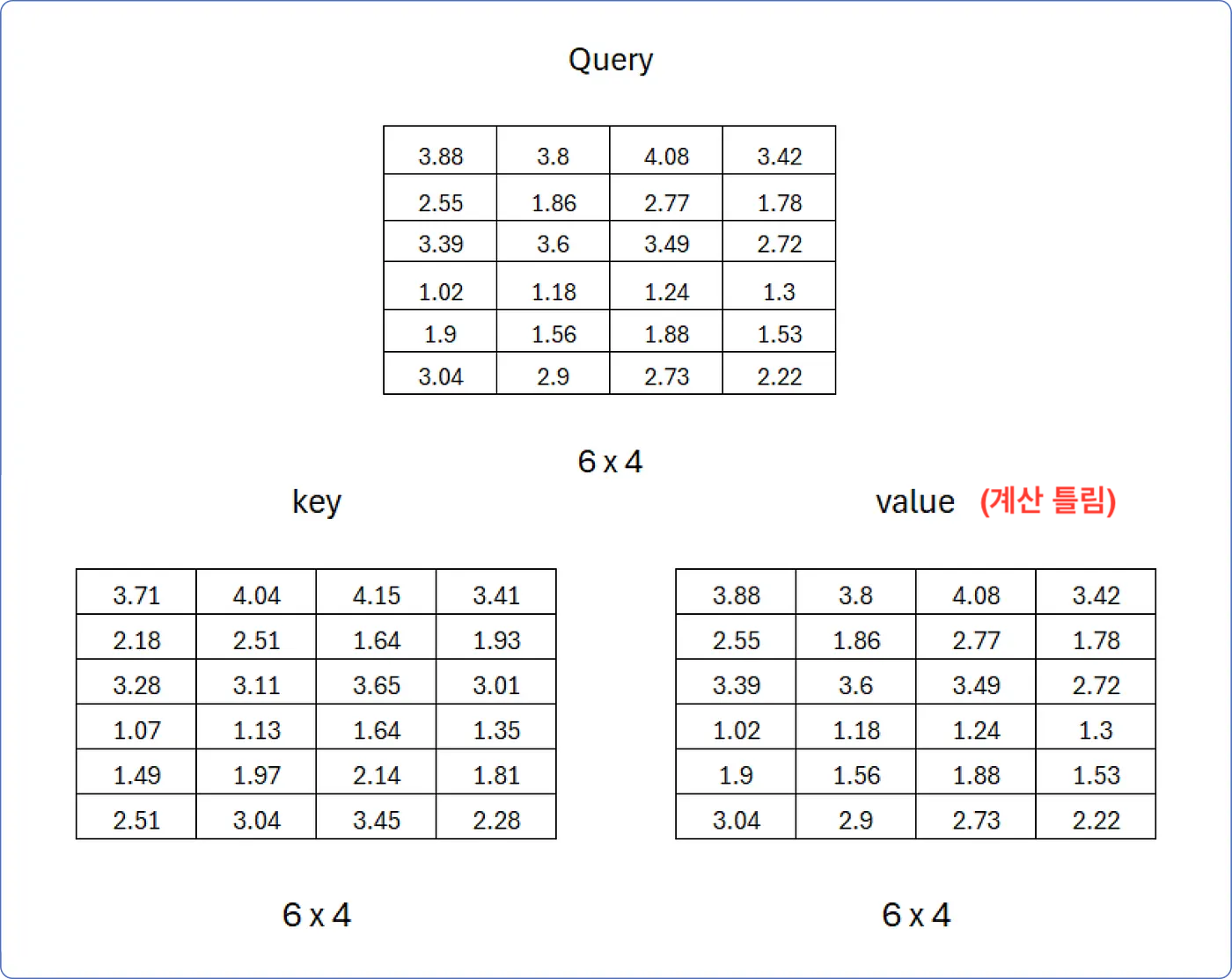
• 이제 Single-Head Attention을 아래의 단계별로 계산해보자.
  

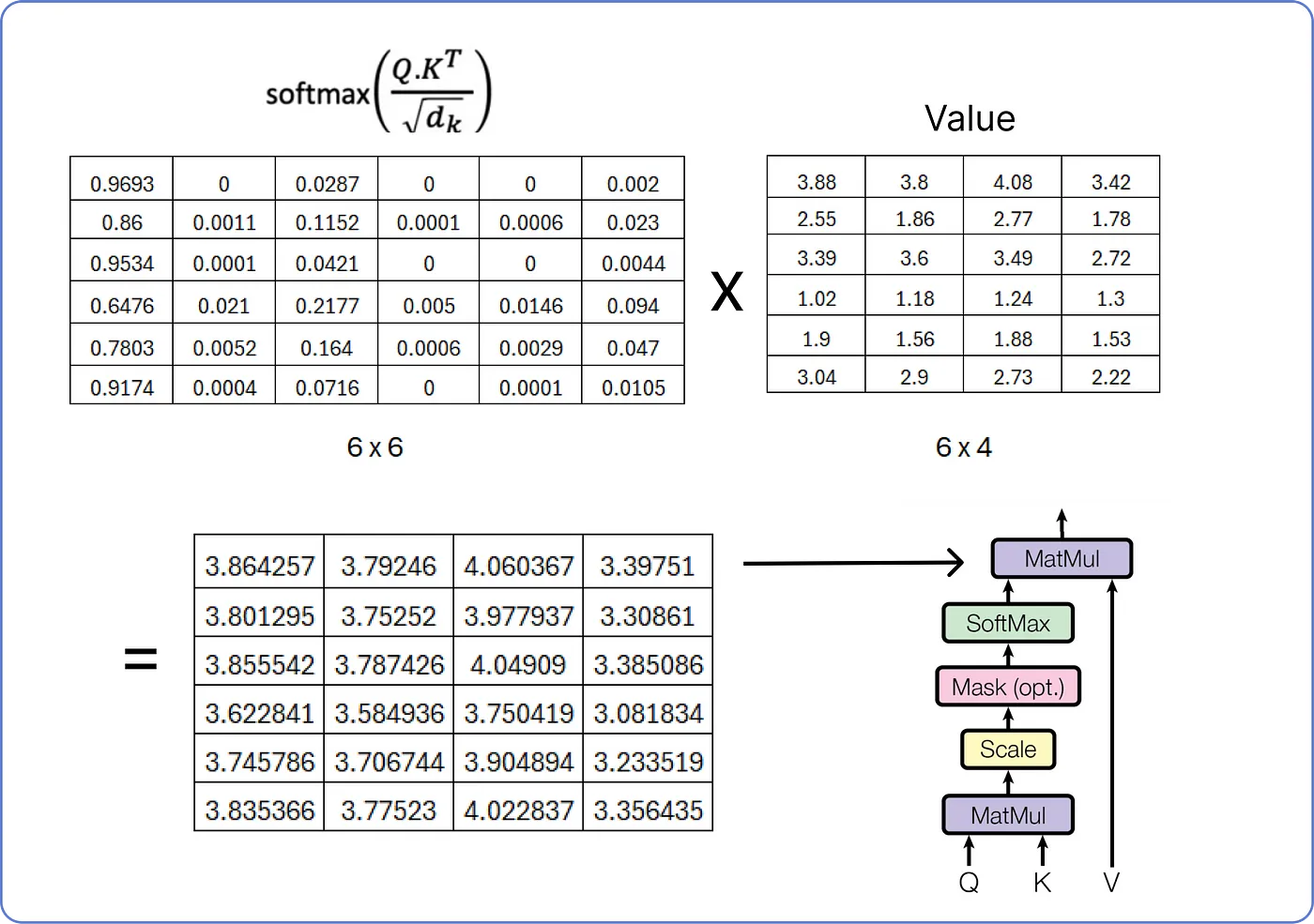
1. MatMul

• Query와 Key의 내적, 즉 $Q \circ K^T$을 계산함으로써 Attention Score를 얻는다.
  

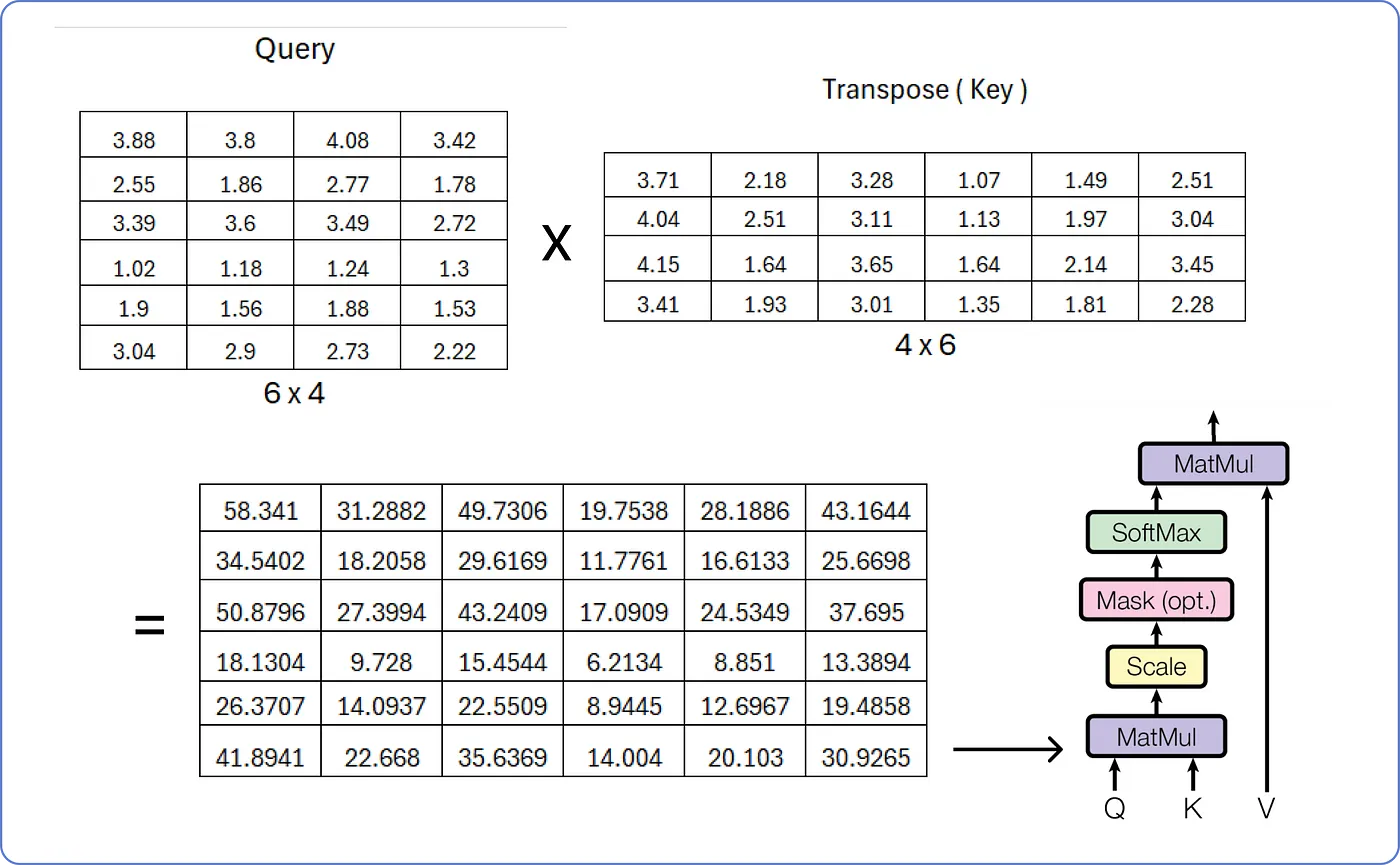
2. Scale

• 이때, Key 벡터의 차원($d_k$)이 커지면 $Q \circ K^T$의 분산이 증가해 Softmax의 출력이 한 값에 편중될 수 있다.
  -> 따라서 $\sqrt{d_k}$로 나누어줌으로써 분산값을 줄인다.
• 이 예제에서 Key 벡터의 차원은 4이므로 $\sqrt{4} = 2$로 나누어준다.
  

3. Mask (opt.)

• Masking은 선택 사항이며, 이 예제에서는 수행하지 않는다.
• Masking은 모델에게 특정 시점 이전에 발생한 일에만 집중하고,
  문장에서 다른 단어의 중요성을 파악하는 동안 미래를 들여다보지 말라고 하는 것과 같다.
• 즉, 모델이 앞을 내다보며 속임수를 쓰지 않고 단계별로 이해하도록 돕는다.

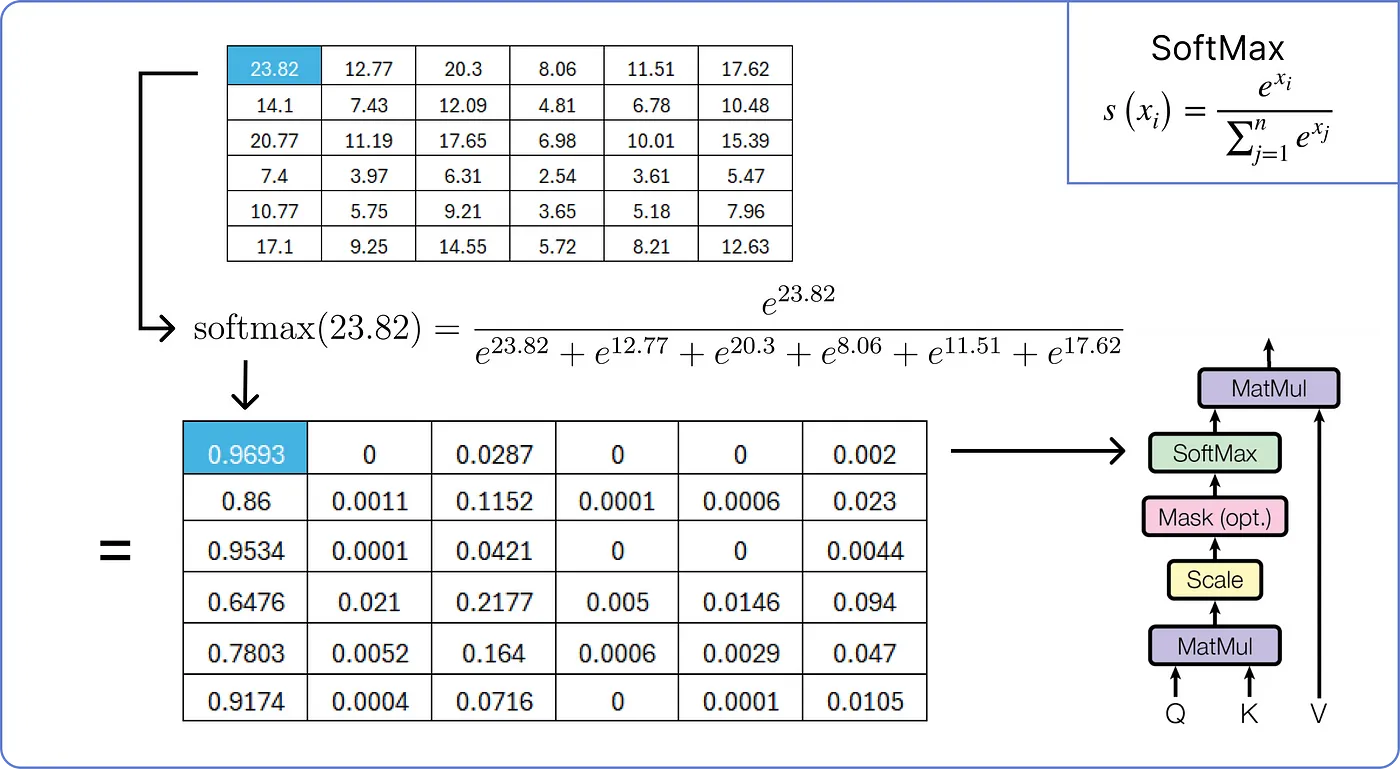
4. Softmax

• Attention Score의 유사도를 0~1의 값으로 정규화하기 위한 과정이다.
• 앞서 구한 Scaled Attention Score에 Softmax 함수를 적용한다.
  

5. MatMul

• 1~4에서 구한 Attention Score와 Value를 내적함으로써 Self-Attention Value를 구할 수 있다.
  

Step 7-2 - Multi-Head Attention

• 여기서 문제는, 하나의 Attention은 하나의 Softmax에 기반한다는 것이다.
  즉, 각 단어들이 단 하나의 다른 단어와 연관된다는 것이다.
• 따라서 여러 Softmax를 활용하기 위해 (여러 개의 Single-Head Attention으로 구성된) Multi-Head Attention을 사용한다.

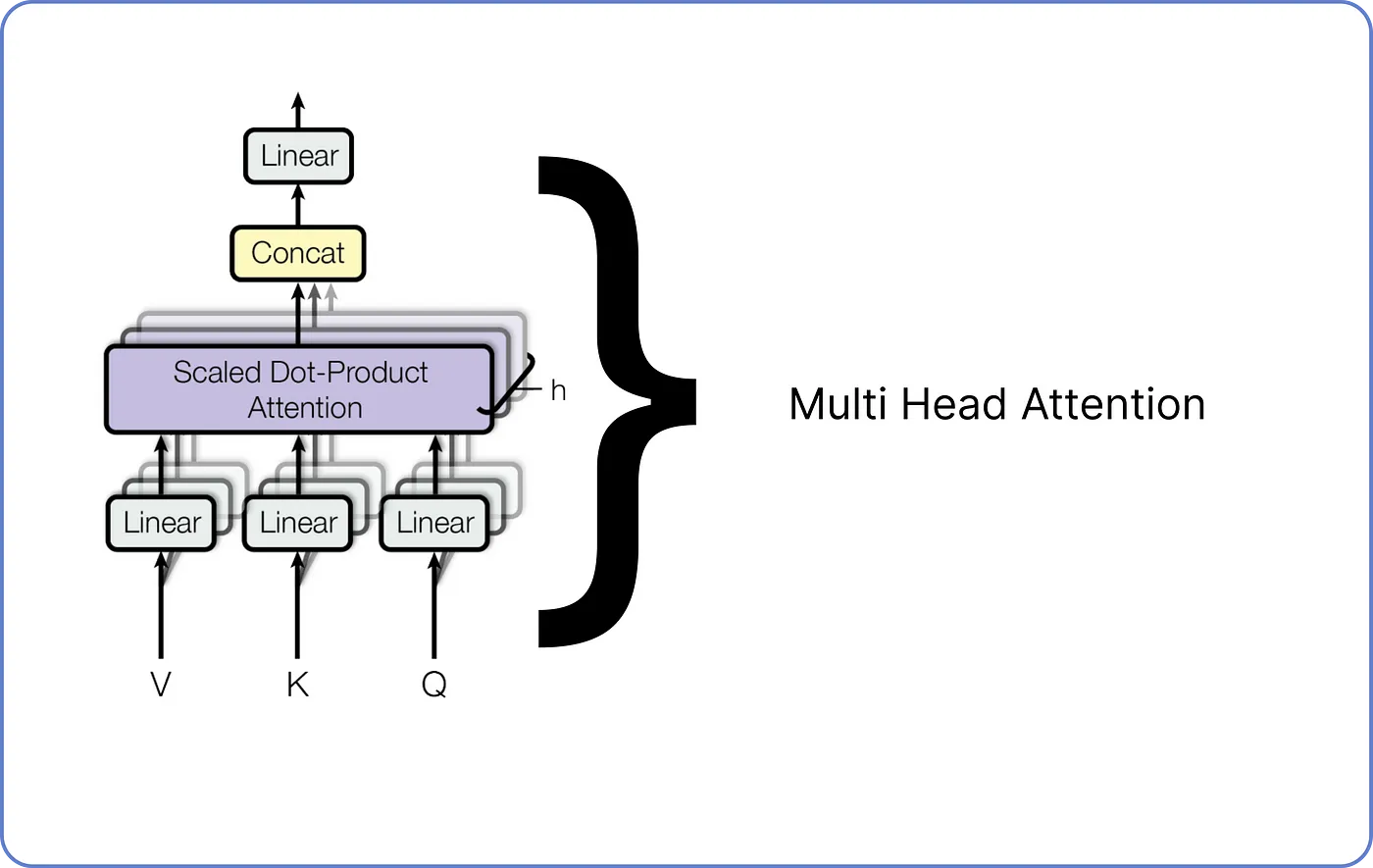
• Single-Head Attention의 출력들을 Concatenate한 뒤,
  

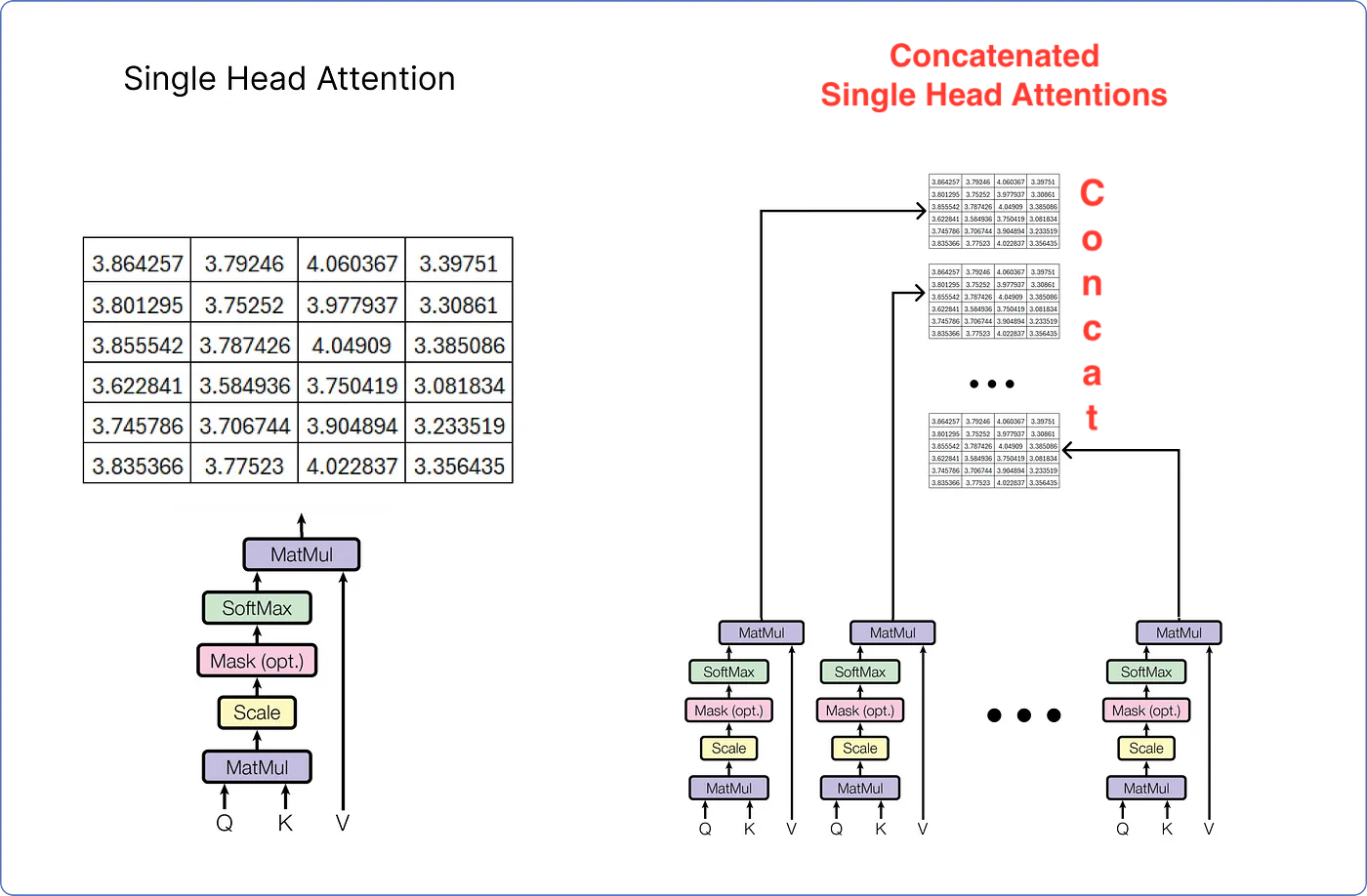
• 선형 변환함으로써 Multi-Head Attention을 수행한다.
• 선형 변환을 위한 행렬 $W^O$는 처음에 무작위 값으로 채워져 있으며, 트랜스포머가 학습함에 따라 업데이트된다.
  

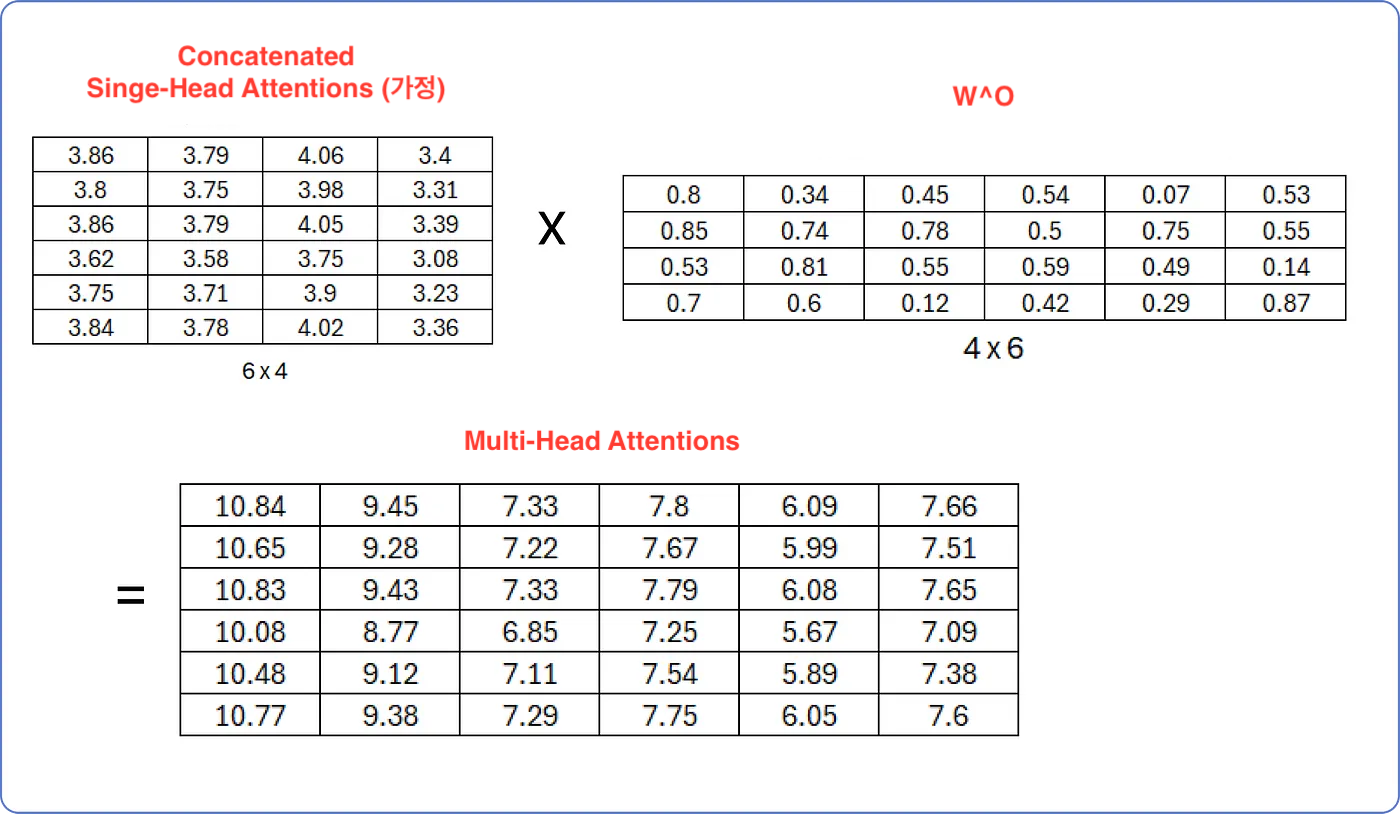
• * 좌측 상단 행렬은 여러 개의 Single-Head Attention이 concat된 행렬이라 가정하자.
• 즉, Multi-Head Attention은 다음의 수식으로 구할 수 있다.
  

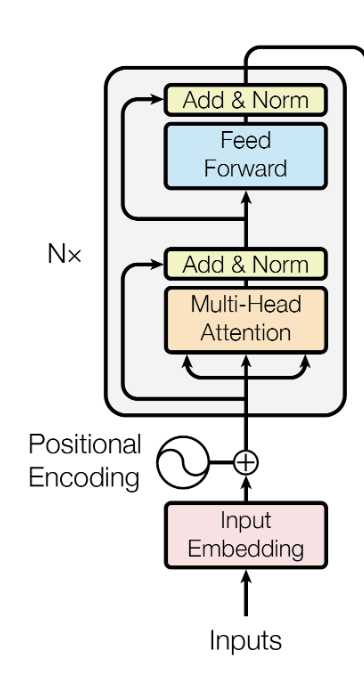
Step 8 - Add & Norm

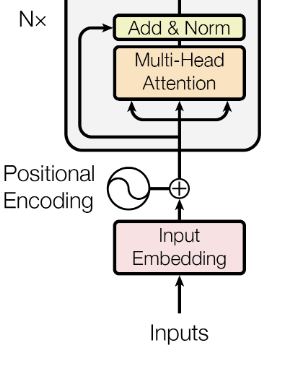
• 인코더 입력 행렬 $X$와 Multi-Head Attention을 더하고 정규화 하는 과정이다.
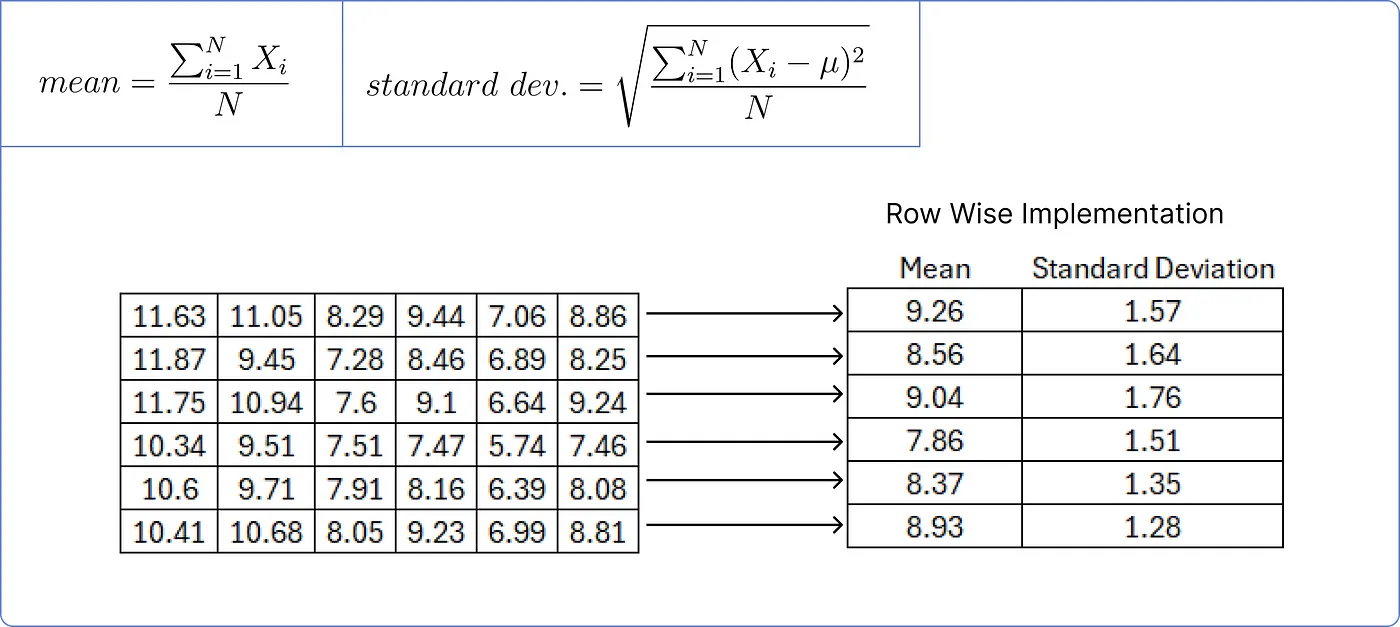
• 먼저 $X$와 Multi-Head Attention을 더하면 다음과 같은 행렬을 얻을 수 있다.
  

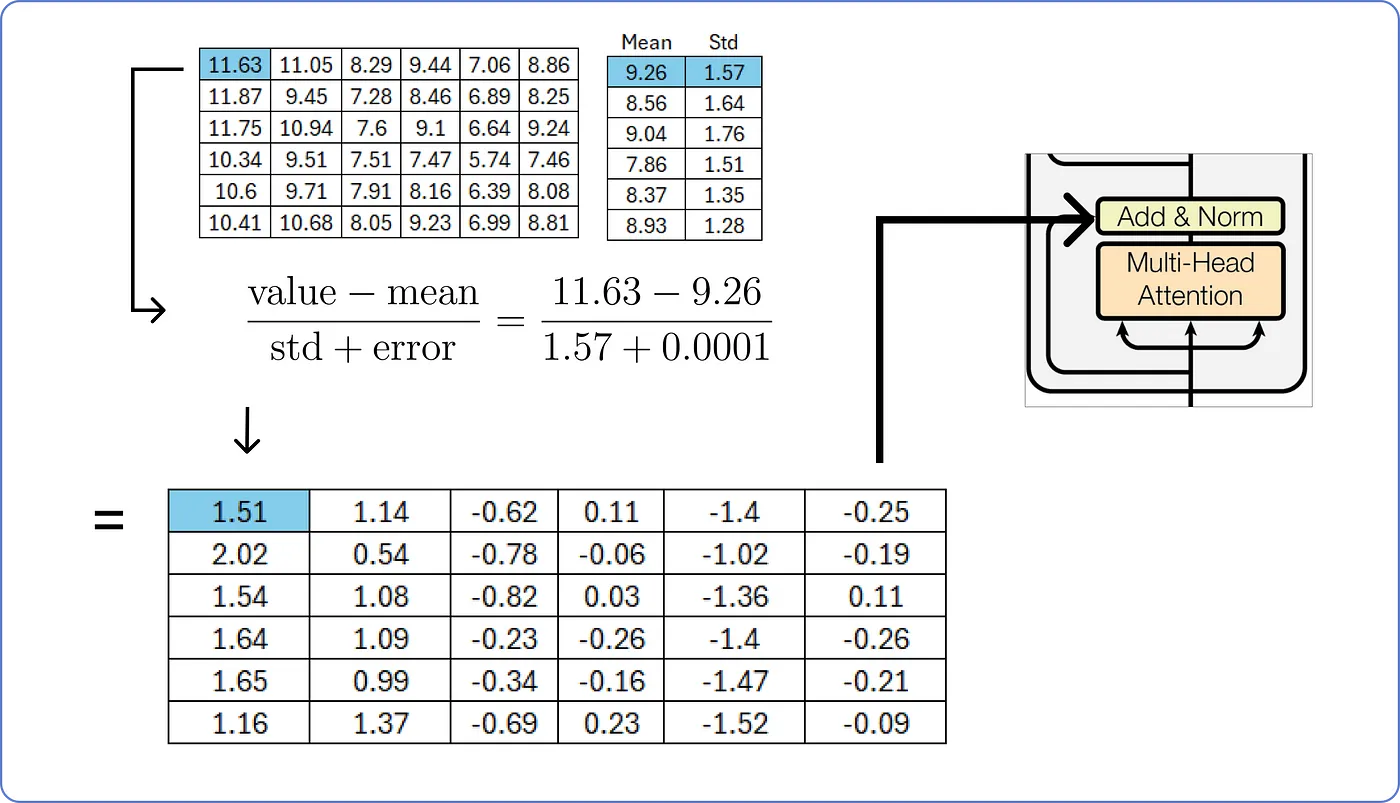
• 이후 행렬을 정규화하기 위해, 각 행에 대한 평균과 표준 편차를 행 단위로 계산한다.
  

• 행렬의 각 값을 해당 행의 평균으로 빼고, 표준 편차로 나눠준다.
• 이때, 분모에 작은 오차값을 더해주면 분모가 0이 되어 무한대로 발산하는 것을 피할 수 있다.
  

Step 9 - Feed Forward Network

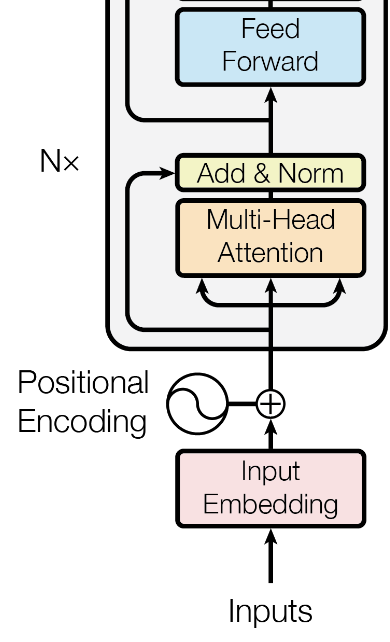
• 행렬을 정규화한 후, Feed Forward Network를 거친다.
• 원래 여러 개의 Linear Layer와 ReLU를 거쳐야 하지만, 이 예제에서는 하나의 Layer만을 다룬다.
  

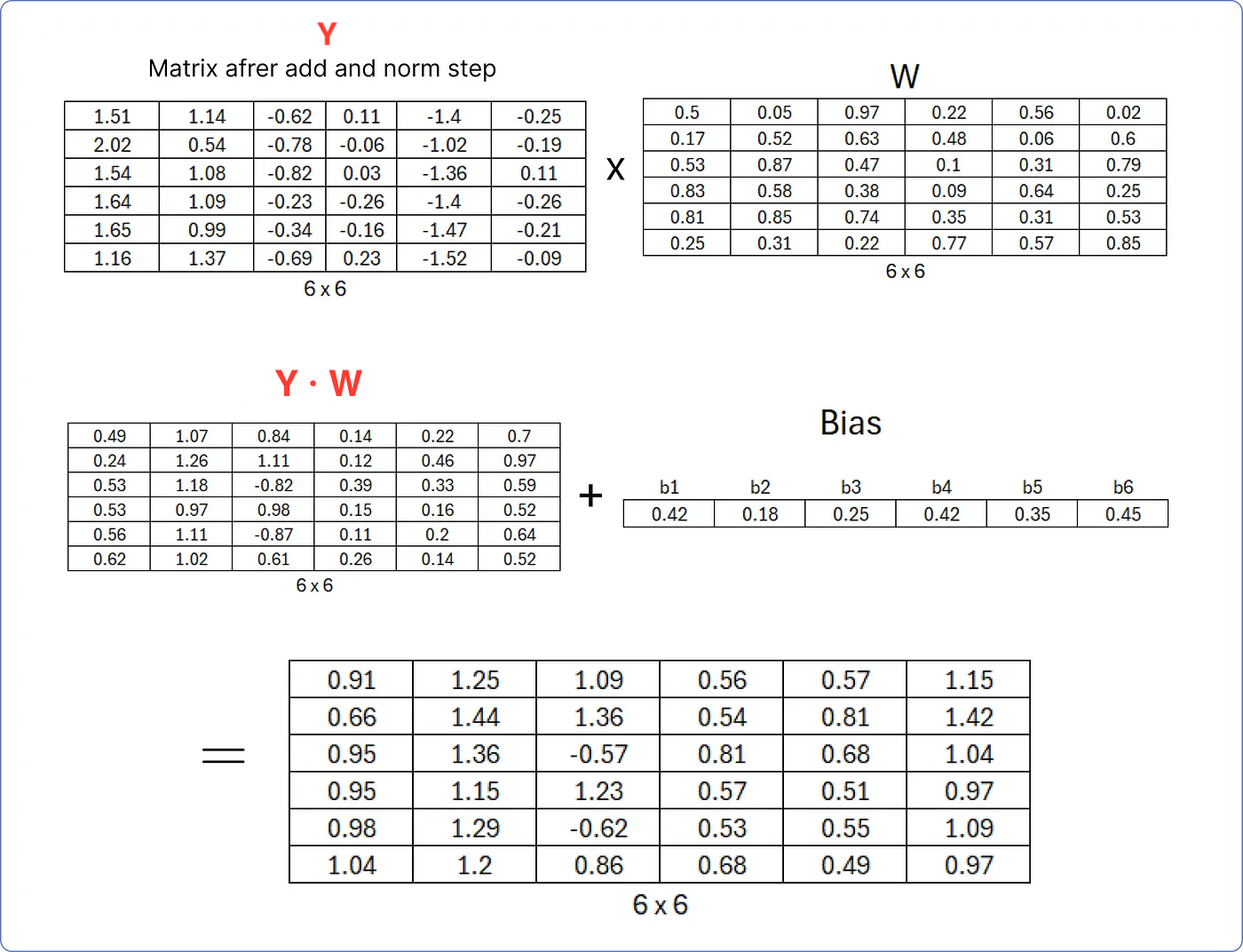
• 먼저, Step 8 의 행렬 $Y$에 선형 가중치 행렬 $W$를 내적해 Linear Layer를 구한 뒤, 편향 $B$를 더한다.
• 이때의 $W, B$는 처음에 무작위 값으로 채워져 있으며, 트랜스포머가 학습함에 따라 업데이트된다.
  

• Linear Layer를 계산한 뒤, ReLU에 통과시킨다.
  

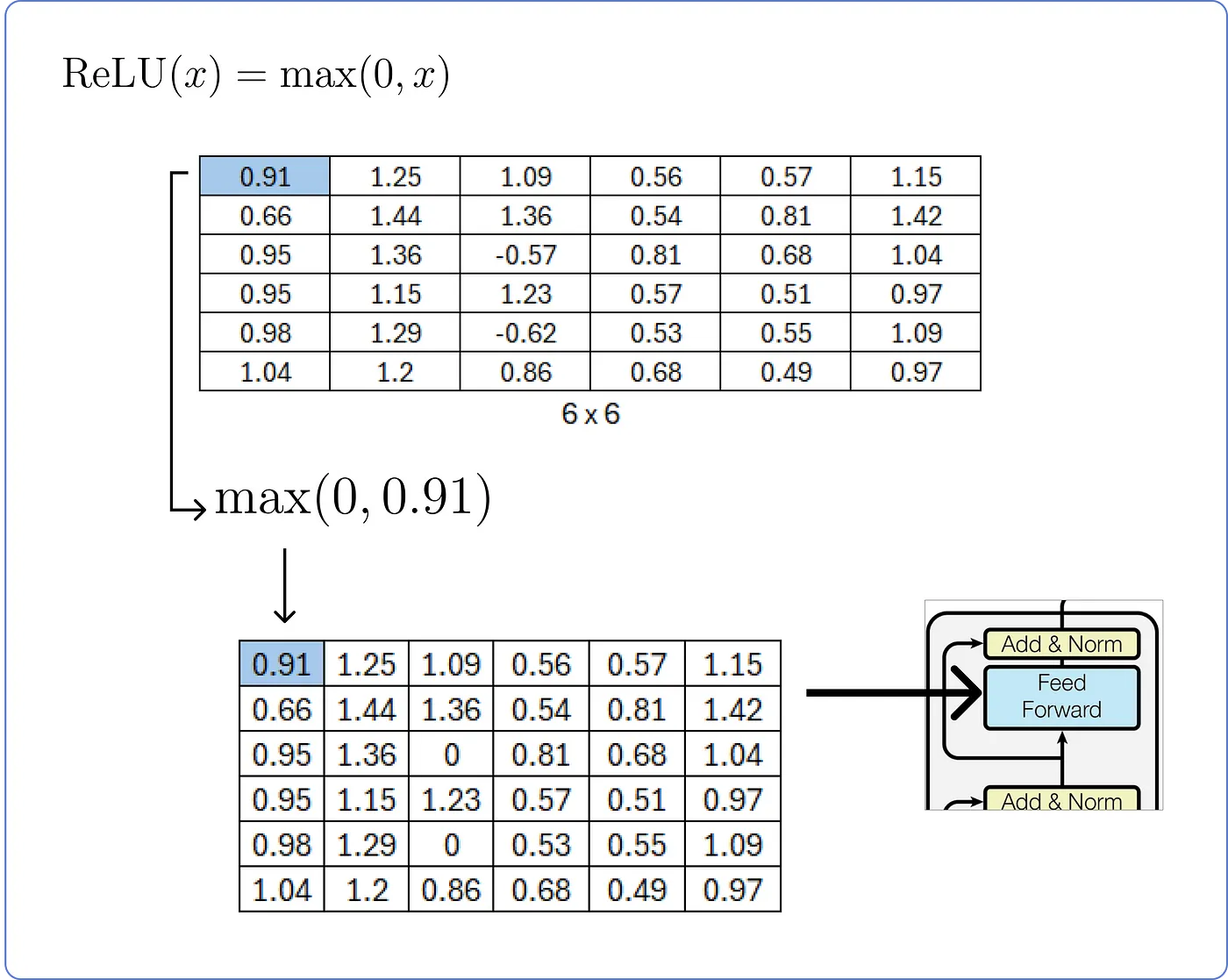
Step 10 - Add & Norm (again)

• Feed Forward Network를 통과하기 전(Step 8), 통과한 후(Step 9)의 행렬을 더하고 정규화한다.
• Step 8에서 그랬던 것처럼, 행 단위로 평균과 표준 편차를 구해 정규화한다.

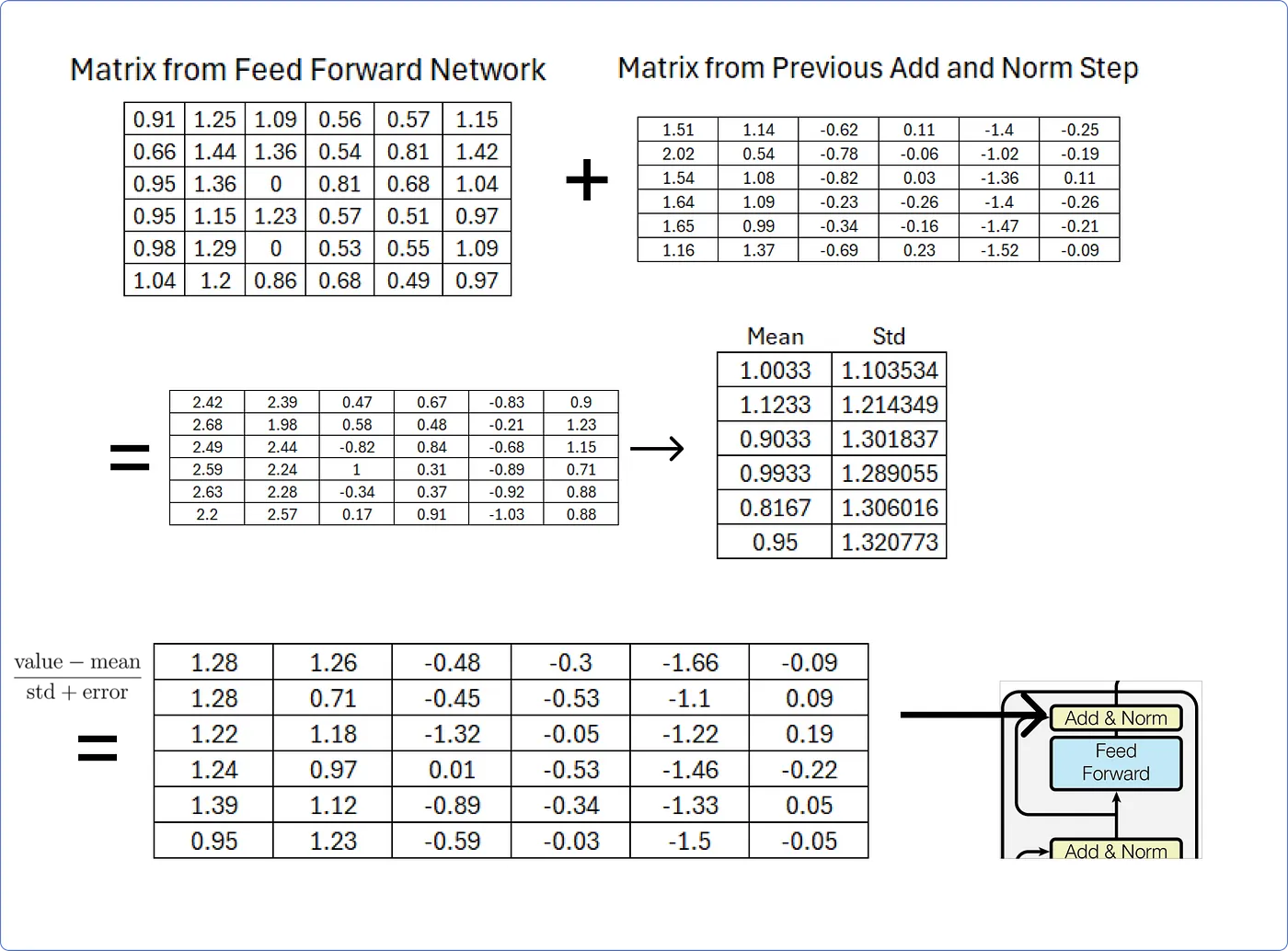
• 여기까지 인코더 부분을 계산해보았다.
• 인코더에서 구한 행렬은 디코더의 Multi-Head Attention의 입력에서 Key와 Value 행렬 역할을 한다.

---

Decoder Part

Step 11 - Decoder Part

• 디코더 부분에서는 인코더에서 수행한 것과 유사한 계산들이 반복된다.
  

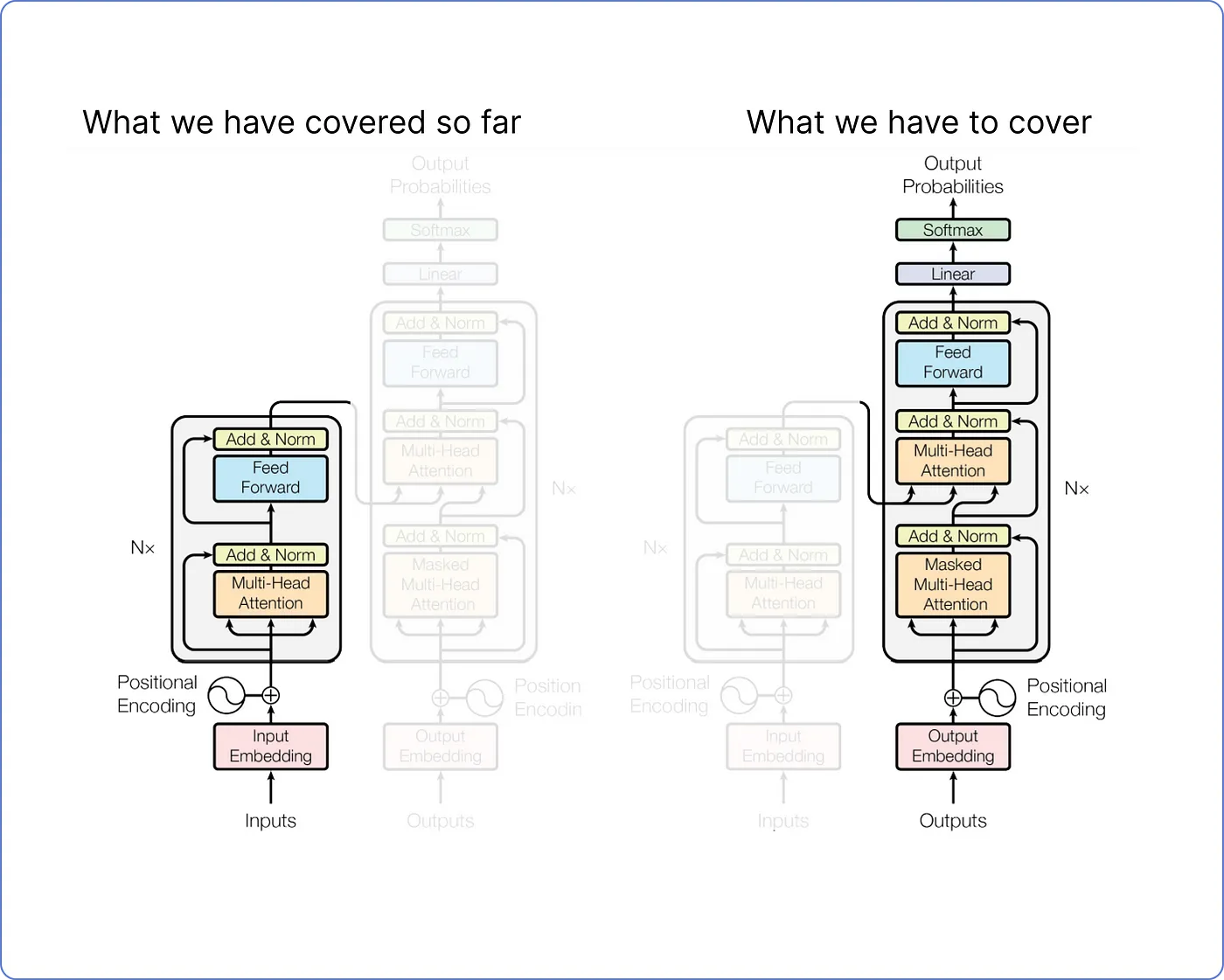
• 디코더에는 두 가지 입력이 있다.

---

Outro

이 글은 개념보다는 수식적 이해에 집중하였다. 다음 글에서는 트랜스포머의 개념적 이해를 다루어보겠다.

계산이 틀린 부분을 직접 수정하고자 하였으나, 수정 사항이 너무 많아 도중에 포기하였다. 너른 양해를 바란다.

원글에 주재걸 교수님의 강의와 다른 부분이 있는데(Multi-Head Attention 등), 이러한 부분은 주재걸 교수님의 강의에 맞게 수정하였다.

참고 자료

• 주재걸 교수님 강의 자료
• https://levelup.gitconnected.com/understanding-transformers-from-start-to-end-a-step-by-step-math-example-16d4e64e6eb1
• https://www.blossominkyung.com/deeplearning/transformer-mha
• https://arxiv.org/pdf/1706.03762
• https://www.youtube.com/watch?v=gJ9kaJsE78k&t=596s