BOJ 11437 : LCA

풀이 요약

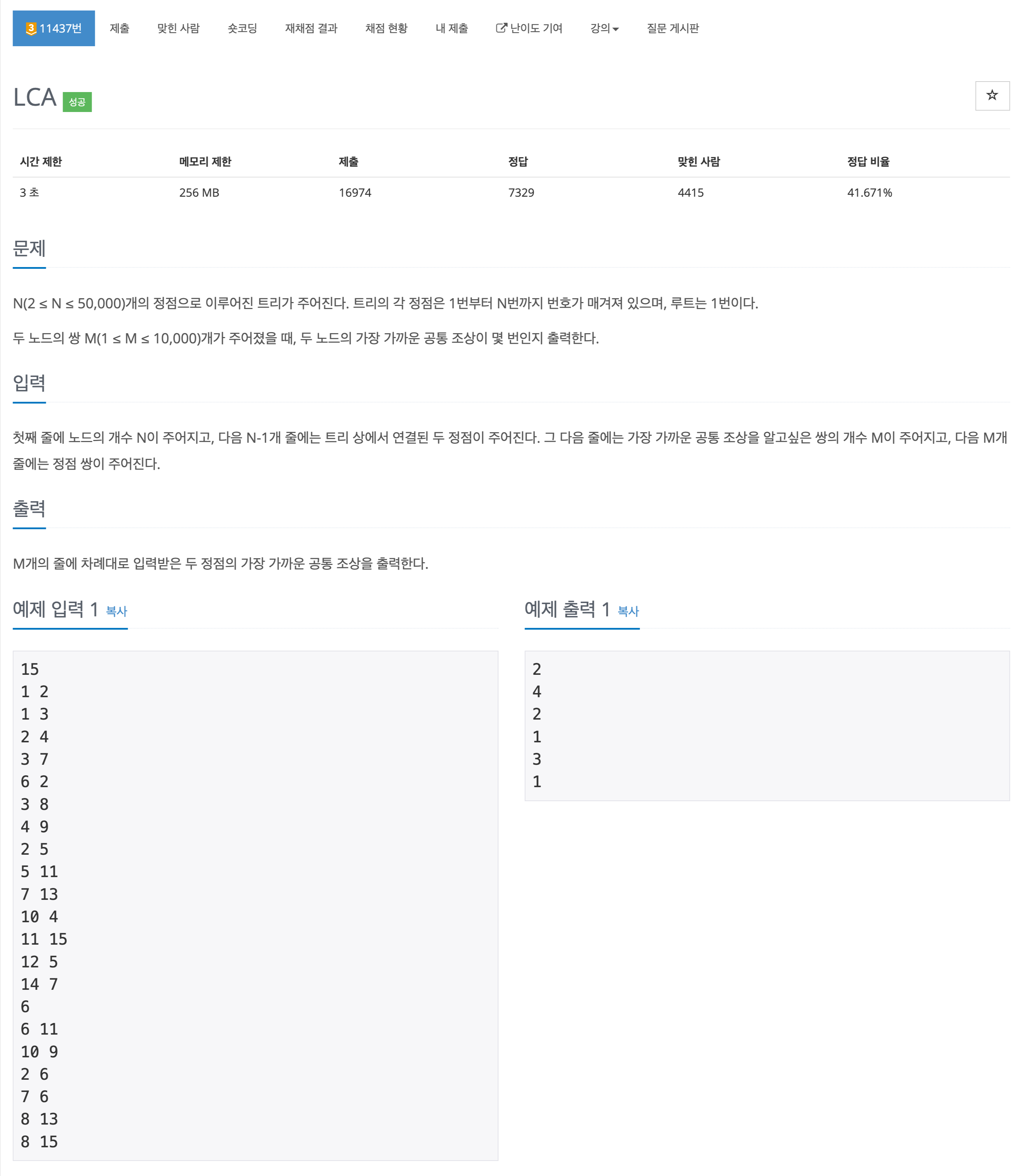
LCA 를 활용하는 문제

풀이 상세

1. 임의의 노드인 $n1$ , $n2$ 가 존재하는 경우, 해당 공통 조상을 찾는 식은 다음과 같다.

2. 먼저 $n1$, $n2$ 의 $depth$ 가 동일한지 확인해야 한다. $n2$ 자체가 $n1$ 부모이거나, 혹은 같이 올라가기 시작하는 경우, 최소 공통 조상을 지나칠 수 있기 때문이다. 만약 $depth$ 가 다르다면, $depth$ 가 더 높은 노드를 부모 노드로 올리면서, 동일하게 맞춰줘야 한다.

3. 노드 간 $depth$ 가 동일하다면, 자신과 연결된 부모 노드를 탐색한다. 이 과정은 동일한 값이 나올 때까지 지속된다.

배운점

• 1번 노드가 루트 노드이며, 예제가 선행 노드들이 부모 노드로 잘 인식되어서, 당연히 자식노드들 보다 부모노드가 먼저 나올 것이라고 생각하였다. 덕분에 다른 케이스에서 트리가 제대로 형성되지 않는 경우가 발생했다. 심지어 타입이 int 라, $0$ 으로 초기화 되어, $0$ 이 $0$ 을 찾는 무한적인 탐색이 진행되었다… (시간초과 이유)

• 일단 리스트에 양방향으로 좌표를 받아둔 뒤 DFS 를 통해, 트리를 제대로 구현하자. 올바르게 정답이 나왔다.

• 임의의 노드 두 깊이를 $N$, $M$ 이라고 한다면, LCA 의 시간복잡도는 $O(NM)$ 이 된다. 이를 조금만 바꾸면 $O(MlogN)$ 으로 줄이는 공식이 존재한다고 한다. 한번 공부해보자.

정답

#include <iostream>
#include <tuple>
#include <vector>
using namespace std;

typedef tuple<int, int, int> tp; // 부모, 본인, depth
const int MAX = 5e5 + 5;
int N, M;
tp a[MAX];
vector<int> v;
vector<int> d[MAX];
bool visited[MAX];
tp tmpB, tmpS;

void output() { cout << get<1>(tmpB) << '\n'; }

void LCA(int n1, int n2) {
    // 더 층이 높은 애 찾기
    tmpB = a[n1];
    tmpS = a[n2];
    if (get<2>(a[n1]) < get<2>(a[n2])) {
        tmpB = a[n2];
        tmpS = a[n1];
    }

    while (get<2>(tmpB) != get<2>(tmpS)) {
        tmpB = a[get<0>(tmpB)];
    }

    while (get<1>(tmpB) != get<1>(tmpS)) {
        tmpB = a[get<0>(tmpB)];
        tmpS = a[get<0>(tmpS)];
    }

    output();
}

void input() {
    cin >> N;
    int n1, n2;
    for (int i = 1; i < N; i++) {
        cin >> n1 >> n2;
        d[n1].push_back(n2);
        d[n2].push_back(n1);
        // (시간초과의 이유)
        // a[1] = make_tuple(0, 1, 1);
        // if (get<1>(a[p]) != 0) {
        //     a[c] = make_tuple(p, c, get<2>(a[p]) + 1);
        // } else if (get<1>(a[c]) != 0) {
        //     a[p] = make_tuple(c, p, get<2>(a[c]) + 1);
        // }
    }
}

void dfs(int p, int depth) {
    visited[p] = true;

    for (int n : d[p]) {
        if (visited[n])
            continue;
        a[n] = make_tuple(p, n, depth + 1);
        dfs(n, depth + 1);
    }
}

void solve() {
    cin >> M;
    int n1, n2;
    for (int i = 0; i < M; i++) {
        cin >> n1 >> n2;
        LCA(n1, n2);
    }
}

int main() {
    input();
    a[1] = make_tuple(0, 1, 1);
    dfs(1, 1);
    solve();

    return 0;
}