BOJ 2263 : 트리와 순회

풀이 요약

트리를 활용한 분할정복 문제. 완전 이진트리가 아니기에, 후위순회에 대한 인덱스 설정을 어떻게 해야할지 엄청 고민했다.

풀이 상세

1. 후위순회의 특성을 활용한다. 후위순회의 특징은 부모노드가 가장 마지막에 불리는 것이며, 답으로 찾아야 하는 전위순회는 부모노드 부터 먼저 불린다.

2. 문제는 왼쪽의 서브트리와 오른쪽의 서브트리를 나누는 것인데, 이것은 중위순회를 통해 구할 수 있다. 해당 임의의 서브트리가 존재하는 경우, 가장 마지막 인덱스가 곧 부모 노드 (혹은 루트 노드) 이다. 이 부모 노드를 기반으로 중위순회를 탐색하여 찾았을 때, 왼쪽 영역이 왼쪽 서브트리, 오른쪽 영역이 오른쪽 서브트리 역할을 하게 된다.

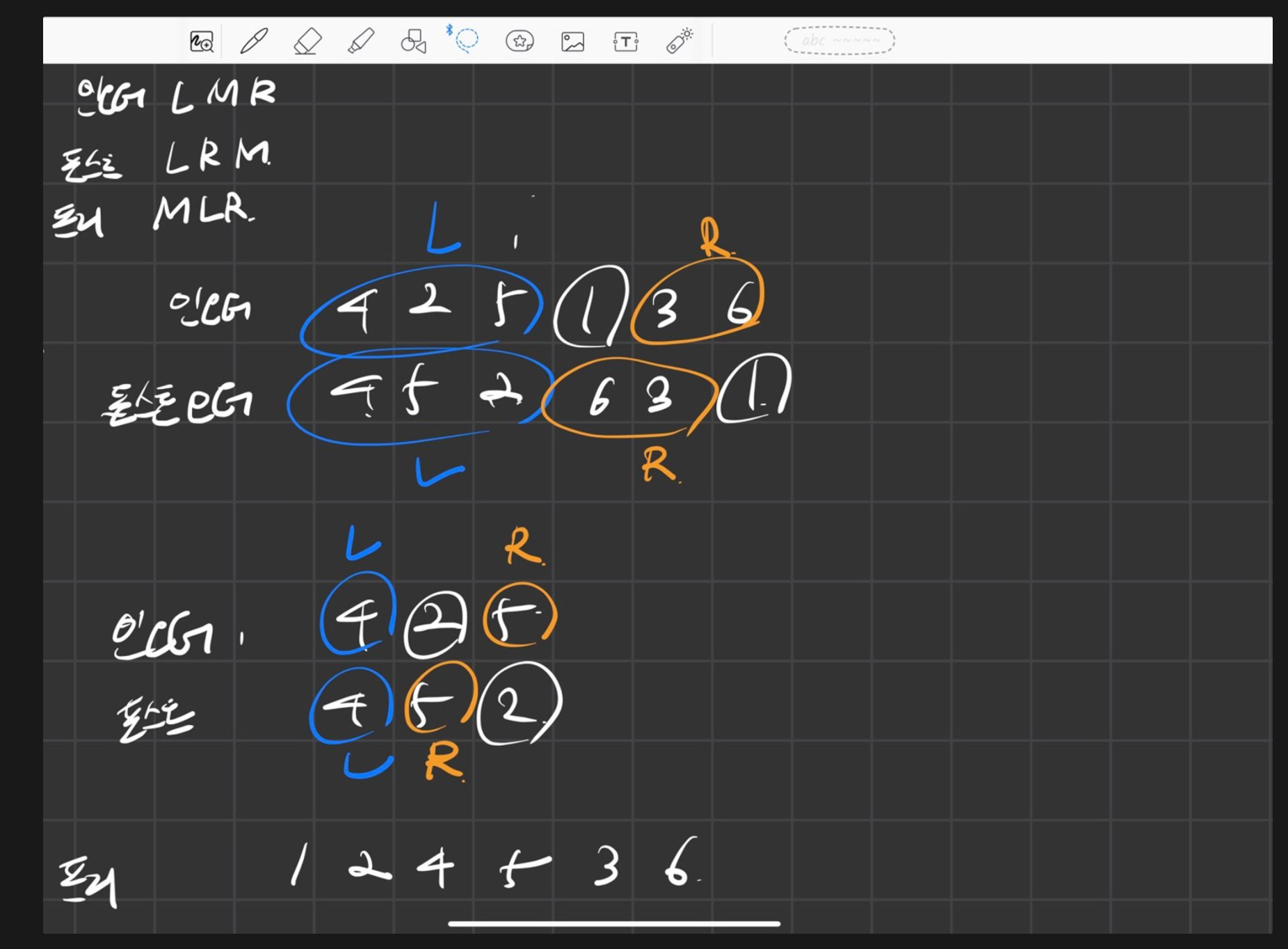
3. 매개변수를 인오더의 시작, 인오더의 마지막, 포스트오더의 시작, 포스트오더의 마지막을 준다.

4. 재귀를 돌면서 현재 서브트리의 부모 노드를 계속 출력한다. 어차피 리프노드만 남게 되어도, 리프 노드 자체가 부모노드가 되기에 루트 - 왼쪽 - 오른쪽 순으로 결국 출력이 된다.

5. 범위 제어는 다음과 같다. 중위순회 탐색을 통해 기준 인덱스를 찾자. 기준을 $mid$ 라고 한다면,

   • 인오더의 범위제어는 생각보다 쉽다. 이분탐색과 같이 mid 의 왼편 전부가, 왼쪽 서브트리이며, 오른편 전부가 오른쪽 서브트리이다.

   • 따라서 인오더의 왼쪽 서브트리는 in_order 의 시작 ~ mid-1 까지이다.

   • 따라서 인오더의 오른쪽 서브트리는 mid+1 ~ in_order 의 마지막 까지이다.

   • 포스트오더의 범위제어는 인오더와 포스트오더가 서브트리 노드와 갯수가 동일하다는 것을 이용하자. 중위순회를 통해 임의의 $mid$ 값이 정해져 있다면 해당 중위순회의 왼쪽 서브트리의 갯수는 mid - in_order의 시작 이 된다.

   • 따라서 포스트오더의 왼쪽 서브트리는 post_order 의 시작 ~ post_order 의 시작 + 중위순회의 왼쪽 서브트리 갯수 - 1 이다.

   • 따라서 포스트오더의 오른쪽 서브트리는 post_order 의 시작 + 중위순회의 왼쪽 서브트리 갯수 ~ post_order 마지막의 바로 앞 직전 까지 이다. post_order의 마지막 은 프리오더의 부모 노드로 이미 출력되므로, 서브트리에 포함될 수 없다.

정답

#include <iostream>
using namespace std;
const int MAX = 1e6 + 4;
int io[MAX], po[MAX], N;
void input() {
    cin >> N;
    for (int i = 0; i < N; i++) {
        cin >> io[i]; // in order;
    }
    for (int i = 0; i < N; i++) {
        cin >> po[i]; // post order;
    }
}

void dvcq(int is, int ie, int ps, int pe) {
    if (is > ie || ps > pe)
        return;
    cout << po[pe] << ' ';
    int mid = -1;
    for (int i = is; i <= ie; i++) {
        if (io[i] == po[pe]) {
            mid = i;
            break;
        }
    }

    dvcq(is, mid - 1, ps, ps + mid - is - 1);
    dvcq(mid + 1, ie, ps + mid - is, pe - 1);
};

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    input();
    dvcq(0, N - 1, 0, N - 1); // divide & conquer
    return 0;
}