BOJ 1722 : 순열의 순서

풀이 요약

기본 순열의 확장판, 수학에 대한 지식을 기반으로 한 백트래킹

풀이 상세

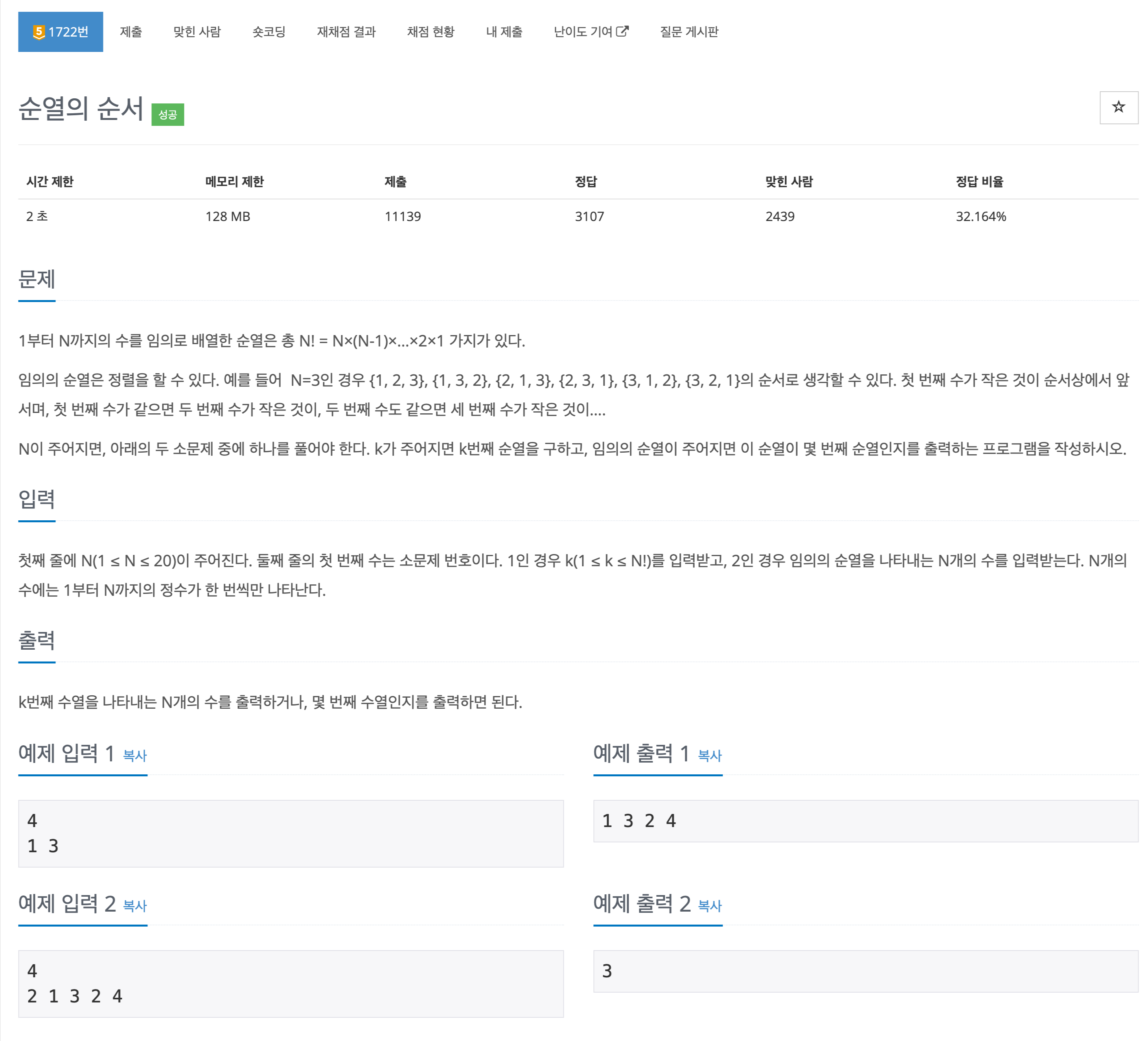
1. 이 문제는 단순 순열 방식으로 하나하나 확인한다면, 시간초과가 나오는 문제이다. 시간제한 : 2초 , 20! = 2.432902e+18

2. 정렬된 순열을 사용한다는 전제하에 나타나는 증명에 대해 파악한 후, 이를 통해 시간을 단축시키는 방법을 찾는 문제이다. 해당 증명은 다음과 같다. (구글링 참조)

   • 임의의 값 $A$ 로 시작하는 순열이 [A,x,x,x] 가 $A$의 자리를 유지한 체 나타낼 수 있는 모든 순열의 경우의 수는 $3!$ 이다.
   • 당연히 임의의 값 $A,B$ 로 시작하는 순열 [A,B,x,x] 가 $A$ 의 자리와 $B$의 자리를 그대로 유지한 체 나타낼 수 있는 모든 순열의 경우의 수는 $(N-2)!$ 인 $2$ 가된다.
   • 첫 자리를 시작으로 매 탐색을 통해 남은 자리수로 나타나는 모든 경우의 수 $(N-idx)!$ 을 업데이트 하여, 순열 혹은 순번을 출력하는 문제이다. 단 해당 순열은 중복 순열이 아니므로 방문 처리를 꼭 진행해주도로 하자.

3. 소규모 문제 1 의 경우에는 주어진 순번을 업데이트 하며, 현재 넣어야 하는 수를 찾는다. 첫 자리에서 부터, 만약 현재 순번보다 $(N-idx)!$ 작은 경우라면, 현재 자리 수에 숫자가 들어갈 수 있는 타이밍이며, 방문 처리를 통해 이전에 값이 이미 먼저 들어갔다면 다음 숫자로 차례를 넘긴다. 참고로 최대 $N$ 의 값이 20 까지 이므로 최대 경우의 수를 생각해서 Long 을 꼭 사용해주자.

4. 소규모 문제 2 의 경우에는 첫 순번 1을 시작으로 주어진 순열을 차례로 방문하며, 남은 자리 수를 순번에 더해간다. 모든 순열을 모두 방문했을 때까지 더한 순번이 해당 순열을 순서대로 진행했을 때 나오는 순번이다.

배운점

• 수학 잘하고 싶다. 구몬 수학이라도 시작해야하나.

정답코드

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    static int N, k;
    static long[] ftrl;
    static boolean[] visited;
    static int[] cmp;
    static long idx;
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static StringTokenizer stk;
    private static void input() throws Exception {
        N = Integer.parseInt(br.readLine());
        stk = new StringTokenizer(br.readLine());
        k = Integer.parseInt(stk.nextToken());
        ftrl = new long[N+1];
        visited = new boolean[N+1];
        ftrl[0] = 1;
        for (int i = 1; i <= N; i++) {
            ftrl[i] = ftrl[i-1]*i;
        }
    }

    private static void solve() {
        cmp = new int[N+1];
        if (k == 1) {
            idx = Long.parseLong(stk.nextToken());
            solve_one();
        } else {
            for(int i=1; i<=N; i++) {
                cmp[i] = Integer.parseInt(stk.nextToken());
            }
            solve_two();
        }
    }

    private static void solve_one() {
        for(int i=1; i<=N; i++) {
            for(int j=1; j<=N; j++) {
                if(visited[j]) continue;
                if(ftrl[N-i]<idx) {
                    idx-=ftrl[N-i];
                } else {
                    cmp[i]=j;
                    visited[j]= true;
                    break;
                }
            }
        }
        for(int i=1; i<=N; i++) {
            System.out.print(cmp[i]+" ");
        }
    }

    private static void solve_two() {
        idx = 1;
        for(int i=1; i<=N; i++) {
            for(int j=1; j<cmp[i]; j++) {
                if(visited[j]) continue;
                idx+=ftrl[N-i];
            }
            visited[cmp[i]]= true;
        }
        System.out.println(idx);
    }

    public static void main(String[] args) throws Exception {
        input();
        solve();
    }
}

오답 코드

평범한 순열이다. 그냥 순열 안 잊어먹으려고 낸건데, 아주 크게 혼났네ㅠ

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    static int N, k, idx;
    static int[] arr, cmp;

    private static void input() throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        StringTokenizer stk = new StringTokenizer(br.readLine());
        k = Integer.parseInt(stk.nextToken());
        arr = new int[N];
        for (int i = 1; i <= N; i++) {
            arr[i-1] = i;
        }
        if (k == 1) {
            idx = Integer.parseInt(stk.nextToken());
        } else {
            idx = 0;
            cmp = new int[N];
            for (int i = 0; i < N; i++)
                cmp[i] = Integer.parseInt(stk.nextToken());
        }
    }

    private static void perm(int d) {
        if (d == N) {
            if (k == 1) {
                if(--idx == 0) printArr();
            } else {
                ++idx;
                if(check()) printIdx();
            }
            return;
        }

        for (int i = d; i < N; i++) {
            swap(i, d);
            perm(d + 1);
            swap(i, d);
        }
    }

    private static void swap(int n1, int n2) {
        int tmp = arr[n1];
        arr[n1] = arr[n2];
        arr[n2] = tmp;
    }

    private static void printArr() {
        for(int i=0; i<N; i++) {
            System.out.print(arr[i]+" ");
        }
        System.exit(0);
    }

    private static void printIdx() {
        System.out.println(idx);
        System.exit(0);
    }

    private static boolean check() {
        int idx = 0;
        while(idx != N) {
            if(arr[idx] != cmp[idx++]) break;
        }
        return idx == N;
    }

    public static void main(String[] args) throws Exception {
        input();
        perm(0);
    }
}