Programmers : 최대공약수와 최소공배수

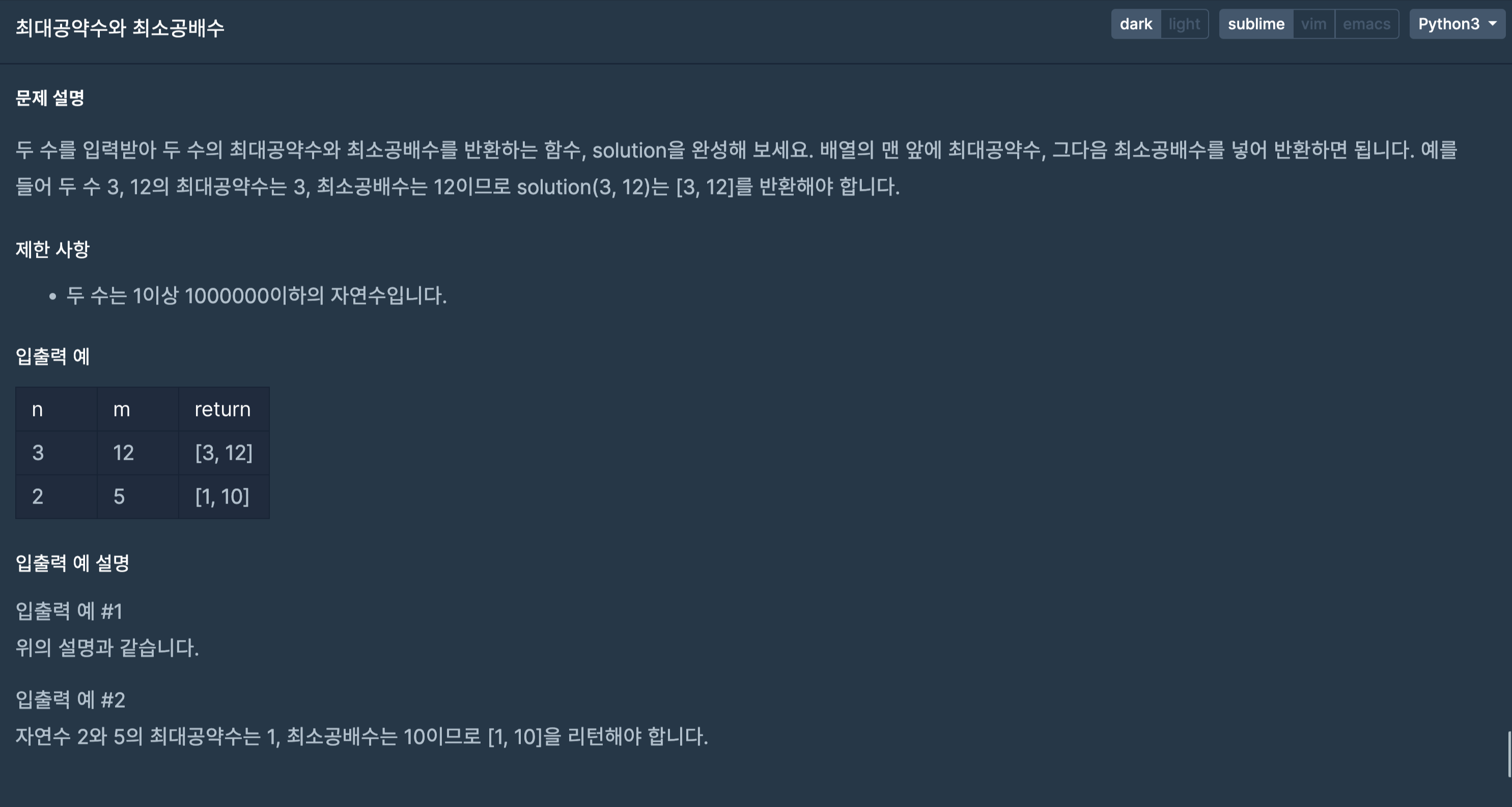
프로그래머스 코딩테스트 연습 - 최대공약수와 최소공배수

풀이 요약

유클리드 호제법.

풀이 상세

1. 유클리드 호제법이란, 최대공약수를 구하는 알고리즘으로, 두 수 $A,B$ 에 대하여 $(A>B)$ $A,B$ 의 최대 공약수는 $B$ 와 $A\%B$ 최대공약수와 동일하다는 것을 전제로 한다.
2. 유클리드 호제법의 증명은 다음과 같다.
   1. 만약 두 수 $A$, $B$ 의 최대공약수를 $G$ 라고 한다면,
      $A = aG$ , $B= bG$ (단 a,b 는 서로소) 로 표현이 가능하며
   2. $A$ 를 $B$ 로 나눈 몫을 $t$ 라고 한다면, 나머지를 $r$ 이라고 하는 경우
      $A= tB+r$ 로 표현할 수 있다.
   3. 이를 $aG, bG$ 로 바꾸면,
      $aG = t(bG) + r$ 이 되고, $r= G(a-tb)$ 의 값이 성립한다.
   4. 나머지 $r$ 은 $G(a-tb)$, $B$ 는 $bG$ 이므로, 역시 최대 공약수 $G$ 가 성립한다.
3. 최소공배수를 찾는 것은 최대공약수가 있다면 쉽다. $(A*B)/G$ 가 바로 최소공배수 값이다.
   1. 두 수 $A,B$ 를 곱하는 경우, 교집합 (최대공약수) 이 2번 곱해지기에 해당 교집합인 $G$ 로 다시 한번 나눠, 온전한 합집합 (최소공배수) 만 나타나게 하는 것이다.

배운점

• 알고리즘을 공부할 때 마다 느끼는 거지만, 늘 이렇게 이해하고 또 금새 잊어먹는다. 어떻게 해야 오래 기억할 수 있을까??
• 수학이랑 친하면 알고리즘을 잘하는 건 맞는 얘기인듯 하다.

코드

#include <string>
#include <vector>

using namespace std;
int GCD(int n, int m) {
    return m ? GCD(m, n%m) : n;
}

vector<int> solution(int n, int m) {
    vector<int> answer;
    answer.push_back(n<m ? GCD(m,n) : GCD(n,m));
    answer.push_back(n*m/answer[0]);
    return answer;
}