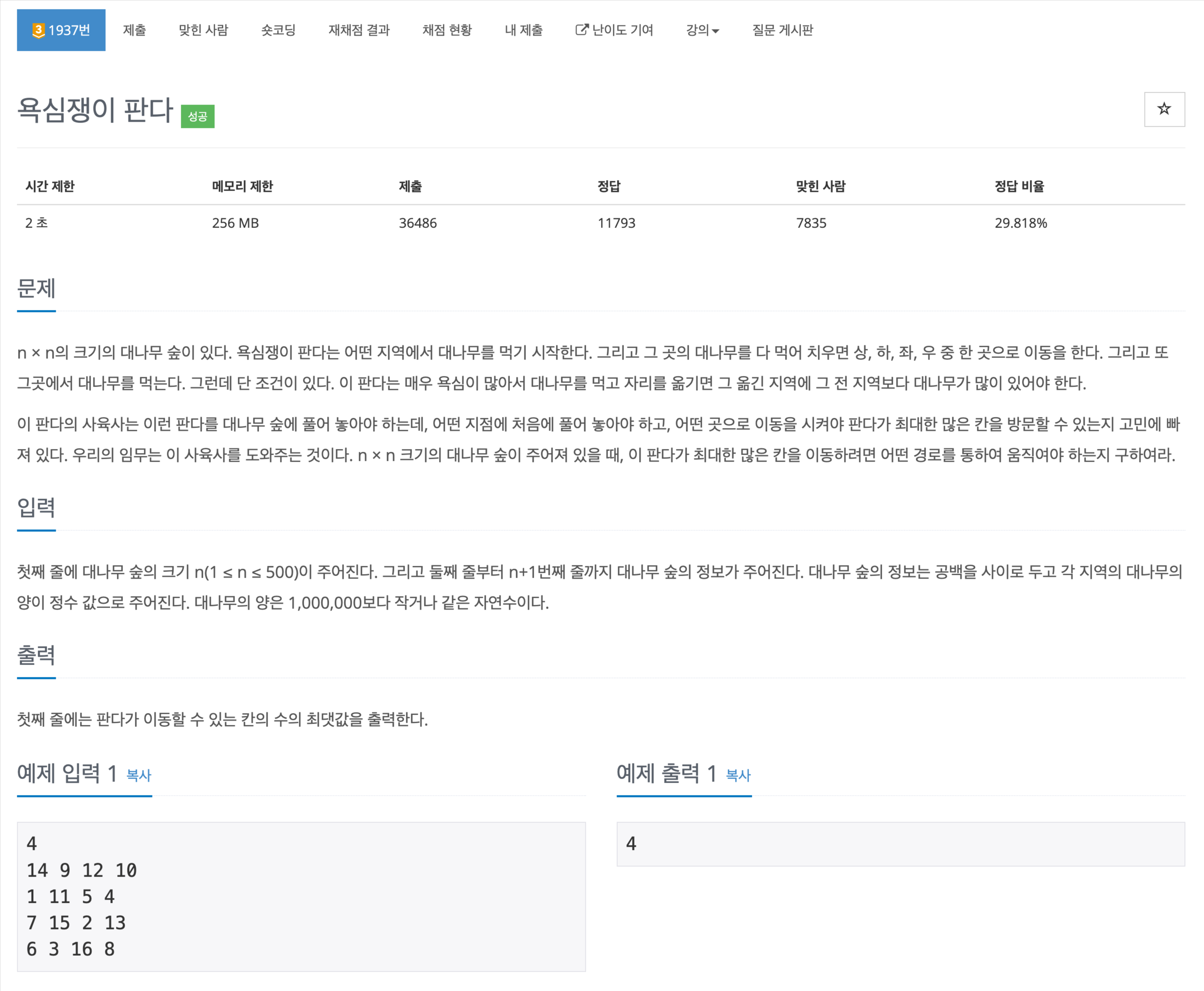
문제

풀이 과정

요약

DP + DFS 를 결합한 문제.
return 하는 재귀를 많이 풀어봐야겠다고 느껴진 문제.

상세

1. 매 좌표마다 DFS()를 호출한다. 만약 현재 좌표 $currPos$ 가 처음 오는 구간이라면 이곳을 1로 만들어준다.

2. 만약 $currPos$ 와 인접한 임의의 좌표 $nextPos$ 의 값이 $x$ 라면, (단, $x > 0$), 현재 좌표 $currPos$ 는 자기 자신을 포함한 $x+1$ 만큼 도달할 수 있게 된다. 단 모든 경우 가운데 언제나 큰 값을 선택할 수 있도록 이를 현재 자신이 가진 좌표와 비교하여 최댓값을 산출한다.

3. 현재 좌표 $currPos$ 에서 도달할 수 있는 최댓값을 이전 좌표까지의 최댓값 들과 비교하는 식으로 진행하다보면 모든 DFS() 가 끝났을 때는 판다가 이동할 수 있는 최대 거리가 나올 것이다.

정답

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    static int[][] map;
    static int[][] dp;
    static int n;
    static final int[] dr = new int[]{-1, 0, 1, 0};
    static final int[] dc = new int[]{0, -1, 0, 1};
    static int ans;

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.parseInt(br.readLine());
        map = new int[n][n];
        for (int i = 0; i < n; i++) {
            StringTokenizer stk = new StringTokenizer(br.readLine());
            for (int j = 0; j < n; j++) {
                map[i][j] = Integer.parseInt(stk.nextToken());
            }
        }

        dp = new int[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                ans = Math.max(ans, DFS(i, j));
            }
        }
        System.out.println(ans);
    }

    private static int DFS(int r, int c) {
        if (dp[r][c] != 0)
            return dp[r][c];

        dp[r][c] = 1;
        for (int d = 0; d < 4; d++) {
            int nr = r + dr[d];
            int nc = c + dc[d];
            if (nr < 0 || nc < 0 || nr >= n || nc >= n) continue;

            if(map[r][c] < map[nr][nc]) {
                dp[r][c] = Math.max(dp[r][c], DFS(nr, nc) + 1);
            }
        }
        return dp[r][c];
    }
}