Programmers : 3x3 타일링

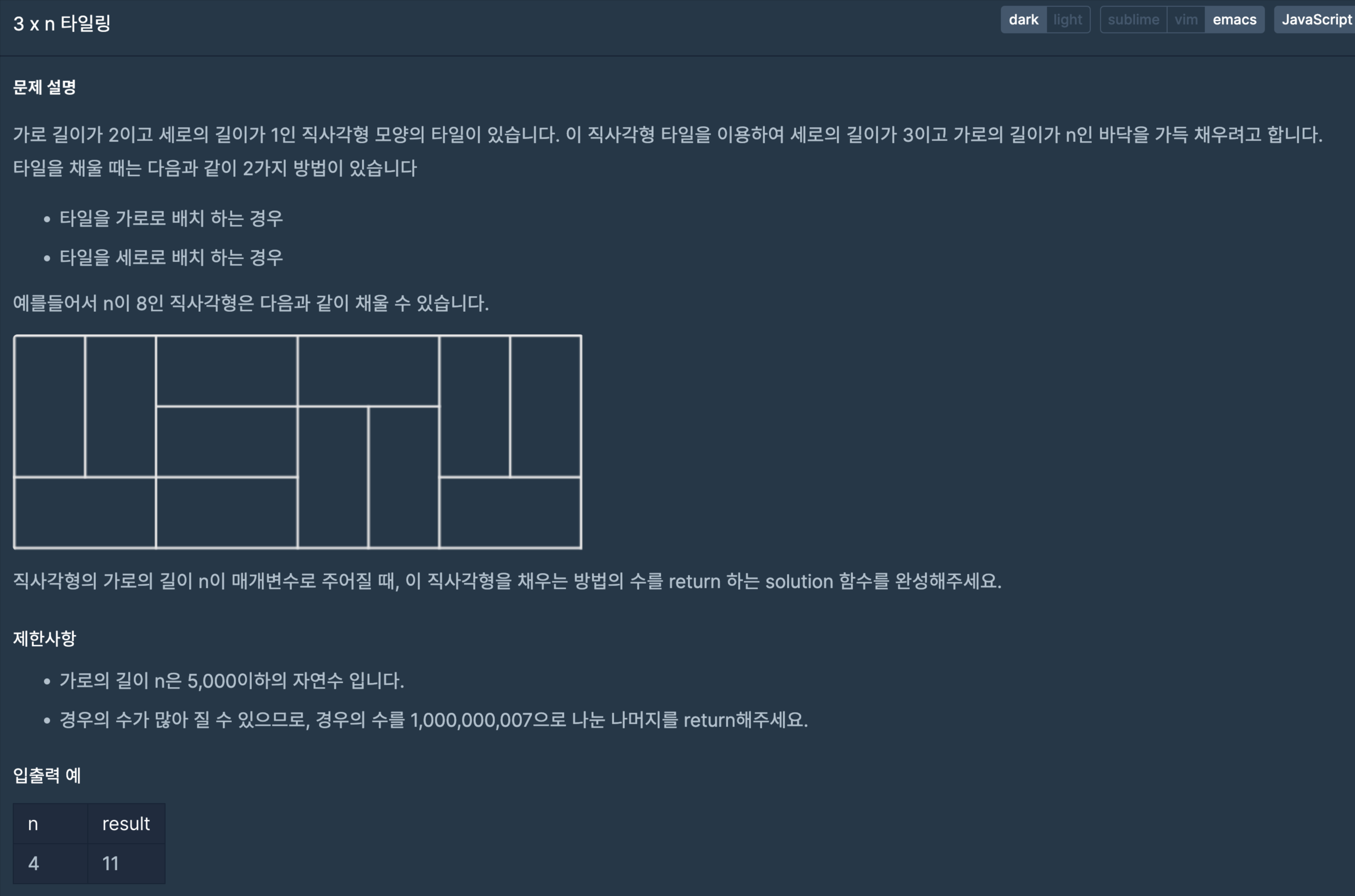
풀이 요약

DP

풀이 상세

1. DP 를 활용한 문제. 먼저 홀수 인 경우에는 절대 배치가 불가능하다는 것을 인지해야한다. 예를들어 가로가 $3$ 인 경우 총 면적은 $9$ 인데, 놓는 직사각형의 면적은 $2$ 이므로, 어떻게 배치를 하여도 $1$ 의 면적이 남게 된다.

2. 따라서 짝수의 가로만 나온다고 가정한다면, 다음과 같은 경우의 수가 나온다.

   • $dp[0]=0$
   • $dp[2]=3$
   • $dp[4] = 11$
   • $dp[6]=41$ (구글 참조)

3. $dp[2]$ 의 값을 초기화 한다면, $dp[4]$ 의 값을 계산할 때, $dp[2]$ 의 값이 사용된다. 만약 $dp[6]$ 의 값을 계산할 때는, $4$ 의 배치와 $2$의 배치를 함께 활용할 수 있기 때문에, $4$의 배치와 $2$의 배치 모두 공간이 남는 곳을 포함하며, 동일한 배치를 한번 더 할 수 있다.

4. 이를 일반화하면 아래와 같은 점화식을 도출할 수 있다.
   $dp[i] = dp[i-1]3 + (2(dp[0]+dp[1]+...+dp[i-2])+2)$

5. 위의 점화식을 이용하여 주어진 n에 대해 DP 알고리즘을 수행하면 정답을 구할 수 있다.

배운점

• reduce() 함수는 시간을 오래 잡아먹는다.

function solution(n) {
  const arr = [0, 3, 11];
  let [sum, div] = [14, 1e9 + 7];
  for (let i = 3; i <= n / 2; i++) {
    const prev = arr[i - 1];
    arr[i] = (prev * 3 + ((sum - prev) * 2 + 2)) % div;
    sum += arr[i];
  }
  return arr[n / 2] % div;
}