

Anomaly Dectection을 요즘에 좀 알아보면서, Time Series Forecasting 분야를 계속 접할 수 밖에 없었고, Transformer의 sequence 적인 특징을 TSF에 사용한 예시가 없을까 하여서 이렇게 찾아보던 중 좋은 논문을 찾게 되었다.
놀랍게도,,, 이 논문은 유명한 모델인 Transformer를 기반으로 하는 모델들이 시계열 예측에 있어서 과연 효과적인지 의문을 가지고 간단한 구조의 모델과 비교하며 transformers가 시간 정보를 학습하지 못함을 증명하는 논문이다...
처음 이 논문을 읽는 분들이라면 유튜브 채널에 먼저 들어가서 이 논문에 대해서 한 번 먼저 들어보길 바란다.
0. Abstract
[상황]
- Long-term Time Series Forecasting(LTSF) 문제의 해결책으로 Transformer 기반의 모델들이 급증
- Transformers는 틀림없이 long sequence의 요소들의 semantic correlations 을 추출하는데 가장 성공적인 해결책
⇒ 그러나 시계열 모델링에서는 연속된 점들의 순서화된 집합에서 시간적 관계를 추출해야 함
[가설과 실험]
- Transformers는 ordering information을 보존하는데 용이한 positional encoding 과 tokens 을 사용하여 sub-series를 embedding
⇒ 이 경우 self-attention 메커니즘의 permutation-invariant 특성으로 인해 필연적으로 temproal information 의 손실이 발생
⇒ Transformers은 LTSF task에 뛰어난 성능보이지 않을 것으로 봄
⇒ 이러한 주장을 평가하기 위해 LTSF-Linear 라는 이름의 매우 단순한 one-layer linear 모델을 통해 비교
[실험 결과]
- 9개의 real-life 데이터셋을 통한 실험 결과에서 현존하는 정교한 Transformer 기반 LTSF 모델들보다 좋은 성능을 보임
- 추가적으로 LTSF 모델의 구성 요소들의 temporal relation 추출 능력에 대한 영향력을 비교
🤔 Transformer 기반의 TSF 모델??
- Informer (AAAI 2021)
- Autoformer (Neurips 2021)
- Pyraformer (ICLR 2022)
- Fedformer (ICML 2022)
- EarthFormer (Neurips 2022)
- Non-Stationary Transformer (Neurips 2022)
- ...
TSF를 위한 Transformer 모델 연구는 많지만,,, 의문이 많고, 성능과 직결되지는 않는다는 평이 많음...
1. Introduction
[Transformer?]
-
Transformer는 NLP, speech recognition, computer vision 등의 분야에서 가장 성공적인 sequence-modeling 아키텍처
-
최근에는 시계열 분석에도 Transformer 기반 솔루션들이 많이 연구되었음
(Ex.)LongTrans,Informer,Autoformer,Pyraformer,FED-former등이 LTSF 문제에서 주목할만한 모델 -
Transformer 의 가장 주요한 부분 : multi-head self-attention (long sequence의 요소들 간의 semantic correlations 을 효과적으로 추출)
✨self-attention의 특징
1) permutation-invariant (입력 벡터 요소의 순서와 상관없이 같은 출력을 생성)
2) anti-order 하여 temporal information loss를 피할 수 없음 -
다양한
positional encoding을 사용하면 몇몇 ordering information 을 보존할 수 있지만, 그 이후 self-attention을 적용하면 이 또한 손실을 피할 수 없음
🤔 단어의 순서를 바꾸더라도 문장의 의미론적 의미는 대부분 유지되는 NLP와 같은 경우 위의 문제를 특징이 크게 상관없으나.. TSF에선 문제가 됨...그렇다면 ,,,
Are Transformers really effective for long-term time series forecasting?
[시계열 데이터의 핵심, 순서]
- 시계열 데이터를 분석하는 경우, numerical data 자체에는 의미가 부족
⇒ 주로 continuous set of points(연속적인 점 집합) 간의 teporal changes(시간적 변화)를 모델링하는 데 관심
⇒ 순서 자체가 가장 중요한 역할을 함!!
[실험 속 오류 제시]
- Transformer 기반 LTSF 솔루션들은 기존 방법론들에 비해 개선된 예측 정확도를 보임
⇒ 그러나 해당 실험에서 non-Transformer 기반의 비교군들은 LTSF 문제에서 error accumulation이 있다고 알려진 autoregressive forecasting 혹은 Iterated
Multi-Step(IMS) forecasting 모델이었음...
[실험 내용]
⇒ 본 논문에선 실제 성능을 확인하기위해 Direct Multi-Step(DMS) forecasting 과 비교
가설: 장기 예측은 물론, 모든 시계열을 예측할 수 있는 것은 아니기 때문에 비교적 명확한 추세(trend) 와 주기성(periodicity) 을 가진 시계열에 대해서만 장기 예측이 가능하다새로운 모델 제시: 선형 모델은 이미 이러한 정보를 추출할 수 있기 때문에, 본 논문에선 매우 간단한LTSF-Linear 모델을 새로운 비교의 기준으로 제시LTSF-Linear 모델: one-layer linear 모델만을 통해 과거 시계열에 대한 회귀를 수행하여 미래 시계열을 직접 예측실험 데이터셋: 교통, 에너지, 경제, 날씨, 재해 예측 등의 널리 사용되는 벤치마크 데이터셋실험 결과:LTSF-Linear는 모든 경우에서복잡한 Transformer 기반 모델보다 성능을 앞섬, 심지어 몇몇 경우에는 큰 차이(20~50%)의 성능을 보임Transformer 기반 모델 문제 발견: (Transformer 기반 모델들의 주장과는 다르게) look-back window sizes 의 증가에도 불구하고 예측 오류가 감소하지 않아 long sequences에서 temporal relations을 추출하는데 실패하는 것을 발견
[contributions]
✅ LSTF task에서의 Transformers의 효과에 대한 첫 번째 의문을 제기한 연구
✅ 간단한 one-layer linear models인 LTSF-Linear와 Transformer 기반 LTSF 솔루션들을 9개의 벤치마크 데이터셋을 통해 비교
✅ LTSF-Linear가 LTSF 문제의 새로운 baseline이 될 수 있음
✅ 기존 Transformer 기반 솔루션의 다양한 측면에 대한 연구 수행
1. long inputs을 모델링하는 능력
2. 시계열 order에 대한 sensitivity
3. positional encoding과 sub-series embedding의 영향력 효율성 비교
✅ 결론적으로, 시계열에 대한 Transformer의 temporal modeling 기능은 적어도 기존 LTSF 벤치마크에서는 과장됨
2. Preliminaries: TSF Problem Formulation

3. Transformer-Based LTSF Solutions
vanilla Transformer 모델을 LTSF 문제에 적용시킬 때에는 두 가지 한계점이 존재
1) original self-attention의 quadractic time/memory complxity
2) autoregressive decoder 설계로 인해 발생하는 error accumulation
Informer는 이러한 문제를 해결하기 위해 complexity를 줄이고, DMS 예측 전략을 사용하는 새로운 Transformer 아키텍처를 제시- 이후 여러 Transformer 기반 모델들이 성능과 효율성을 개선하였고, 이러한 현재 Trasnformer 기반 LTSF 솔루션의 설계 요소를 요약하면 다음과 같음

[1] Time series decomposition
- data preprocessing 과정에서 zero-mean normalization 은 흔하게 사용
Autoformer에서 seasonal-trend decomposition 을 각 neural block 이전에 처음으로 적용
+ 시계열 분석에서 raw data를 더욱 predictable하게 만드는 standard method
+ input sequence에서 moving average kernels 을 통해 시계열 데이터의 trend-cyclical component 를 추출
+ trend component와 origina sequence의 차이는 seasonal component 로 간주된다는 것FEDformer는 전문가의 전략과 다양한 kernel sizes의 moving average kernels로 추출한 trend components를 혼합한 형태를 제시
[2] Input embedding strategies
-
Transformer 아키텍처의 self-attention layer는 시계열의 position information 을 보존하지 못함
⇒ 그러나 시계열의 local positional information 즉 시계열의 ordering은 매우 중요 (+ hierarchial timestamps (week, month, year), agnostic timestamps (holidays and events)와 같은 global temporal information 또한 유익한 정보) -
시계열 inputs의 temporal context 를 강화하기 위해 SOTA Transformer 기반 모델들은 여러 embedding을 input sequence에 활용
+ fixed positional encoding channel projection embedding learnable temporal embeddings
+ temporal convolution layer를 통한 temporal embeddings learnable timestamps
[3] Self-attention schemes
- Transformers는 paired elements 간의 semantic dependencies 를 추출하기 위해 self-attention 메커니즘 활용
- 최근 연구에서는 vanilla Transformer의 O() time/memory complexity를 줄이기 위해 두 가지 전략 제시
1.LogTrans와Pyraformer는 self-attention 메커니즘에 sparsity bias 를 도입
⇒LogTrans는 Logsparse mask 를 사용하여 computational complexity를 O(LlogL)로 감소
⇒Pyraformer는 hierarchically multi-scale temporal dependencies 를 포착하는 pyramidal attention 을 통해 time/memory complexity를 O(L)로 감소
2.Informer와FEDformer는 self-attention matirx에 low-rank property를 사용
⇒Informer는 ProbSparse self-attention 메커니즘과 self-attention distilling operation 을 통해 complexity를 O(LlogL)로 감소
⇒FEDformer는 random selection으로 Fourier enhanced block 과 wavelet enhanced block 을 설계해 complexity를 O(L)로 감소
⇒Autoformer는 original self-attention layer를 대체하는 series-wise auto-correlation 설계
[4] Decoders
-
vanilla Transformer decoder는 autoregressive한 방법으로 outputs을 생성해 특히 long-term predictions에서 느린 추론 속도와 error accumulation 발생
-Informer는 DMS forecasting을 위한 generative-style decoder 를 설계
-Pyraformer는 fully-connected layer를 Spatio-temporal axes와 concatenating하여 decoder로 사용
-Autoformer는 최종 예측을 위해 trend-cyclical components와 seasonal components의 stacked auto-correlation 메커니즘을 통해 재정의된
decomposed features를 합침
-FEDformer는 최종 결과를 decode하기 위해 frequency attention block을 통한 decomposition scheme를 사용 -
Transformer 모델의 핵심 전제는 paired elements 간의 semantic correlations
✔️ self-attention 자체는 permutation-invariant하며 temproal relations을 모델링하는 능력은 input tokens과 관련된 positional encoding에 크게 좌우됨
✔️ 시계열의 numerical data를 고려해보면, 데이터 사이에는 point-wise semantic correlations 가 거의 없음 -
시계열 모델링에서 가장 중요한 부분은 연속적인 데이터들의 집합에서의 temporal relations 이며, 데이터 간의 순서가 Transformer의 핵심인 paired
relationship보다 중요한 역할을 수행 -
positional encoding와 tokens을 사용하여 sub-series를 embedding하면 일부 ordering information을 보존할 수 있지만, permutation-invariant한 self-
attention 메커니즘의 특성상 필연적으로 temporal information loss가 발생
4. An Embarrassingly Simple Baseline
LTSF-Linear의 기초 수식은 weighted sum 연산을 통해 미래 예측을 위해 과거 시계열 데이터를 직접 회귀하는 것
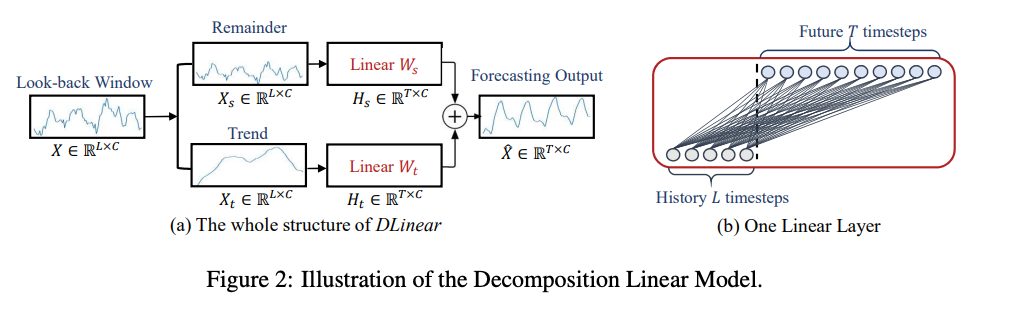
5. Experiments
5.1 Experimental Settings
| Dataset
- 9개의 다변량 real-world 데이터셋 활용
- ETTh1, ETTh2, ETTm1 ETTm2, Traffic, Electricity, Weather, ILI, Exchange-Rate
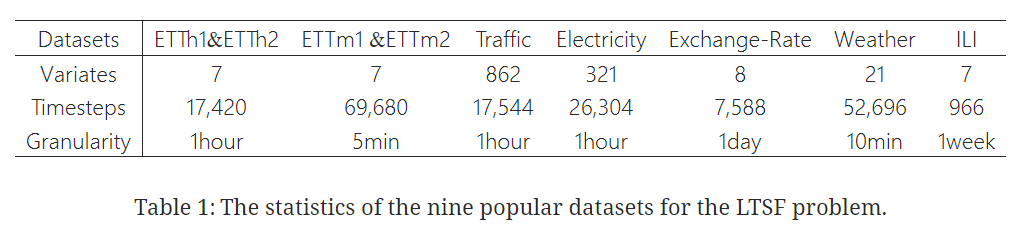
| Evaluation Metric
- Mean Squared Error(MSE) Mean Absolute Error(MAE)
| Compared Method
- 5개의 Transformer 기반 방법론 :
FEDformer,Autoformer,Informer,Pyraformer,LogTrans - naive DMS 방법론
Closest Repeat : look-back window의 마지막 값을 반복
5.2 Comparison with Transformers
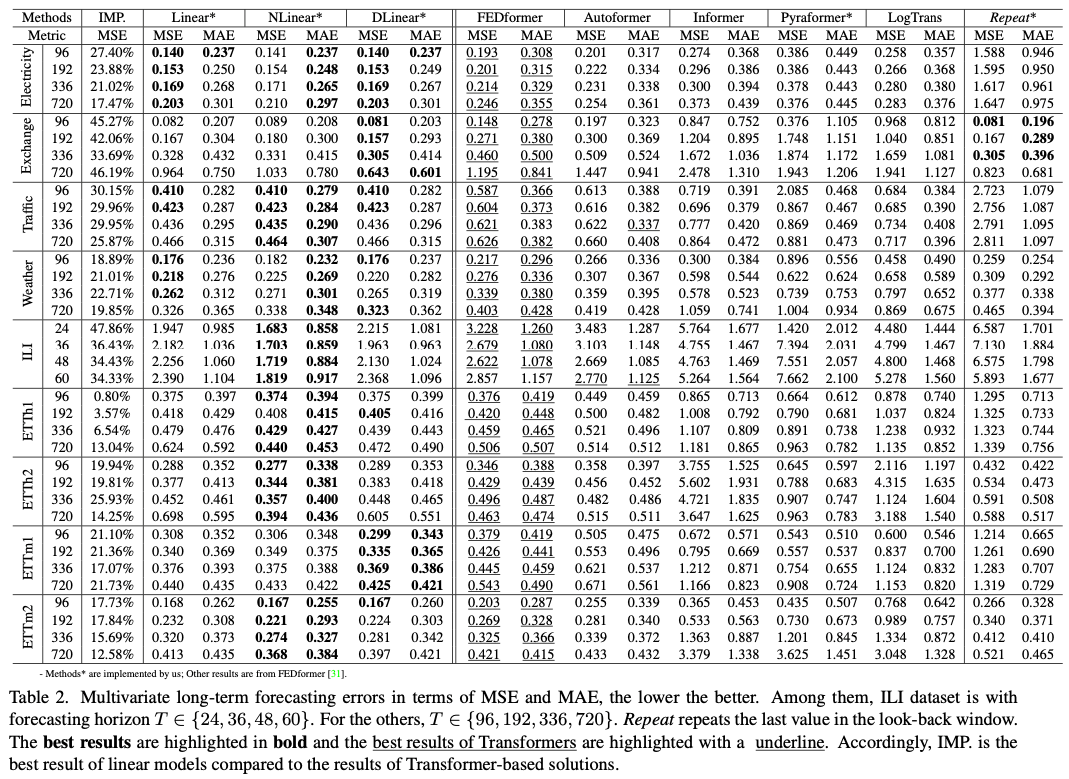
✔️ LSTF-Linear는 변수 간의 correlations을 모델링하지 않았음에도 불구하고, SOTA 모델인 FEDformer를 대부분의 경우 multivariate forecasting에서 약
20%~50% 높은 성능을 보임
✔️ NLinear와 DLinear는 distribution shift와 trend-seasonality features를 다루는 능력에서 우세
✔️ univariate forecasting의 결과에서도 LTSF-Linear가 여전히 Transformer 기반 LTSF 솔루션들과 큰 차이를 보임
✔️ Repeat 모델은 long-term seasonal data(e.g, Electricity and Traffic)에서 가장 좋지 않은 성능을 보였지만, Exchange-Rate 데이터셋에선 모든 Transformer
기반 모델들보다 나은 성능을 보임
++++ 이는 Transformer 기반 모델들이 학습 데이터의 갑작스러운 change noises에 overfit하여 잘못된 trend 예측으로 이어져 정확도가 크게 저하될 수 있음
++++ Repeat은 bias가 존재 X
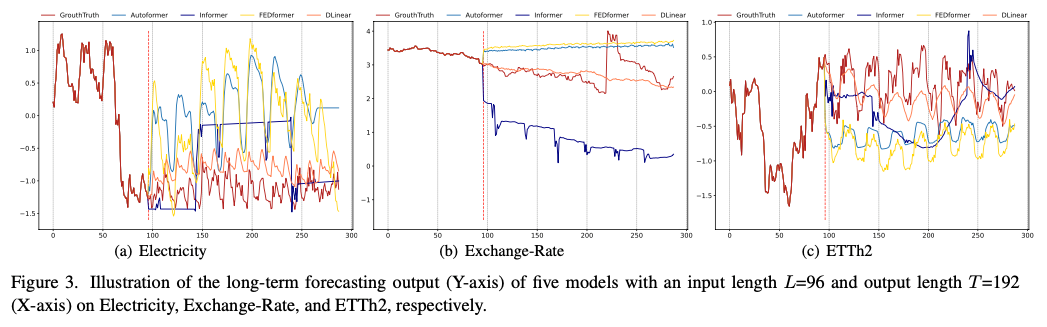
✔️ 3개의 데이터셋에 대한 Transformer 기반 모델들과 LTSF-Linear 모델의 예측 결과
✔️ Electricity(Sequence 1951, Variate 36), Exchange-Rate(Sequence 676, Variate 3), ETTh2(Sequence 1241, Variate 2)
✔️ 해당 데이터셋은 각기 다른 temporal patterns을 보임
✔️ input의 길이가 96 steps이고, output horizon이 336 steps일 때 Transformer는 Electricity와 ETTh2 데이터셋에서 미래 데이터의 scale과 bias를 포착하는데 실패
✔️ 또한 Exchange-Rate 데이터셋에서도 적절한 trend를 예측하지 못함
기존 Transformer 기반 솔루션이 LTSF 작업에 적합하지 않다는 것을 나타냄
5.3 More Analyses on LTSF-Transformers
💡 Can existing LTSF-Transformers extract temporal relations well from longer input sequences?
- look-back window size 는 과거 데이터로부터 얼마만큼을 학습할 수 있는지를 결정하기 때문에 예측 정확도에 많은 영향을 끼침
- 강한 temporal relation 추출 능력을 가진 강력한 TSF 모델은 더 큰 look-back window sizes를 통해 더 좋은 결과를 얻어낼 수 있어야 함
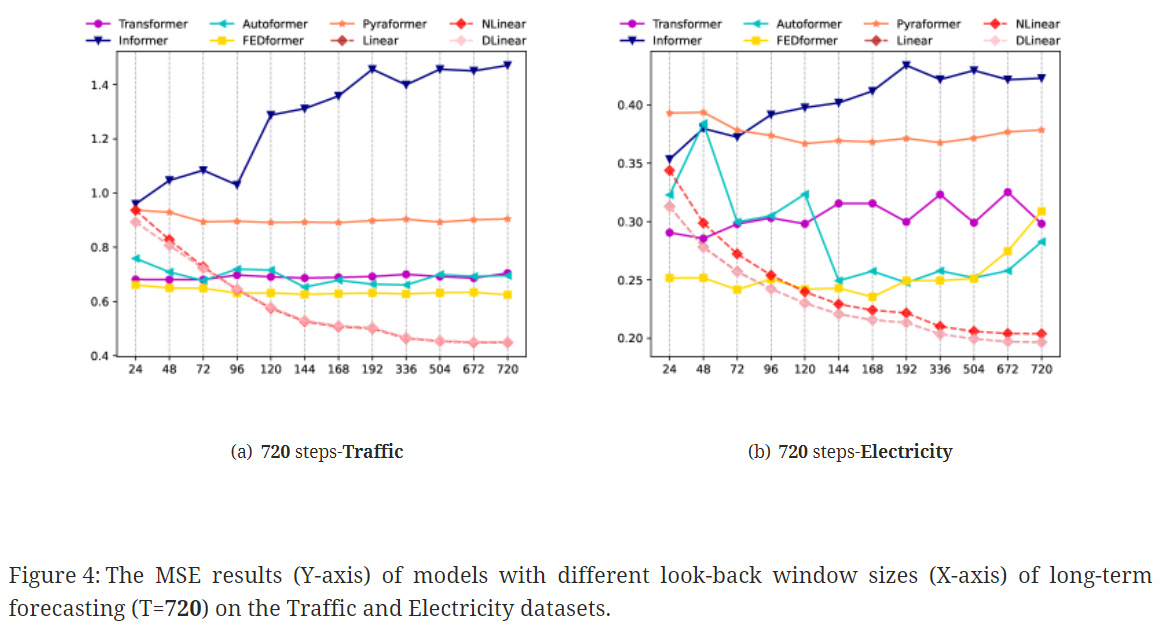
✔️ Transformer 기반 모델들의 성능은 기존 연구의 결과와 동일하게 look-back window size가 커지면서 성능이 악화되거나 안정적으로 유지
✔️ 반면 LTSF-Linear 모델은 look-back windows sizes가 커짐에 따라 성능이 향상
💡 What can be learned for long-term forecasting?
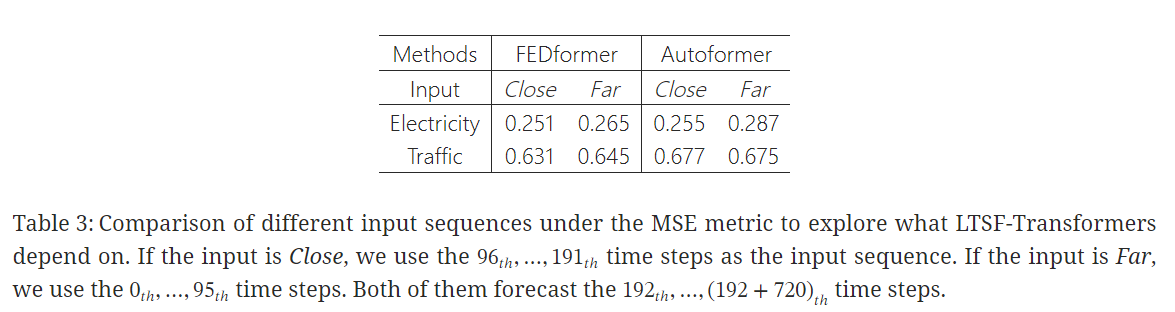
실험 결과,,
✔️ SOTA Transformers의 성능은 Far setting에서 조금씩 떨어지는데, 이는 모델이 인접한 시계열 시퀀스에서 유사한 temproalinformation만 포착한다는 것을 의미
✔️ 데이터셋의 내재적 특성을 파악하는 데 일반적으로 많은 수의 파라미터가 필요하지 않으므로, 하나의 파라미터를 통해 periodicity를 나타낼 수 있음
✔️ 너무 많은 파라미터를 사용하는 것은 overfitting을 유발할 것이고, 이는 LTSF-Linear의 성능이 Transformer보다 좋았던 것을 일부분 설명
💡 Are the self-attention scheme effective for LTSF?
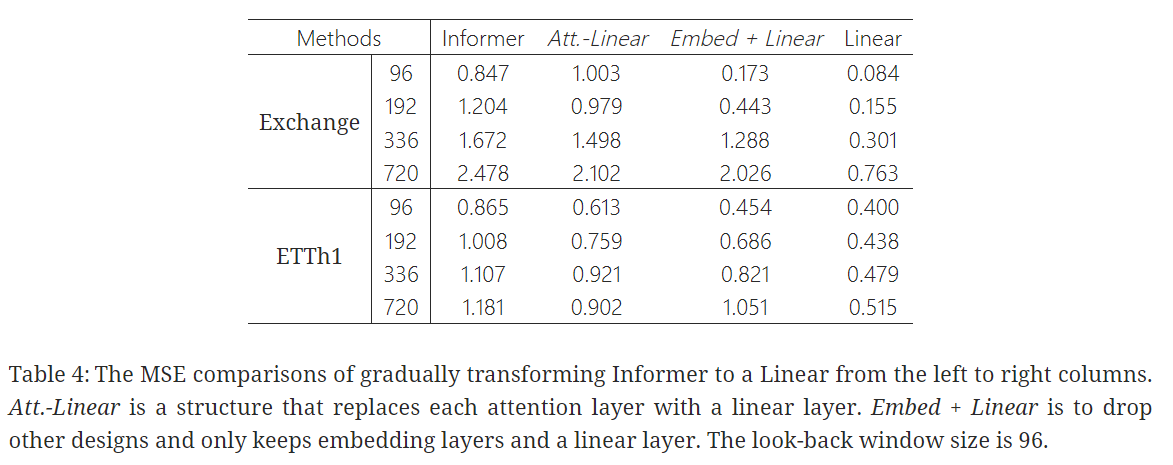
✔️ Informer의 성능은 점진적으로 단순화할수록 향상되어 LTSF 벤치마크에서는 self-attention 체계 및 기타 복잡한 모듈이 필요하지 않음을 나타냄
💡 Can existing LTSF-Transformers preserve temporal order well?
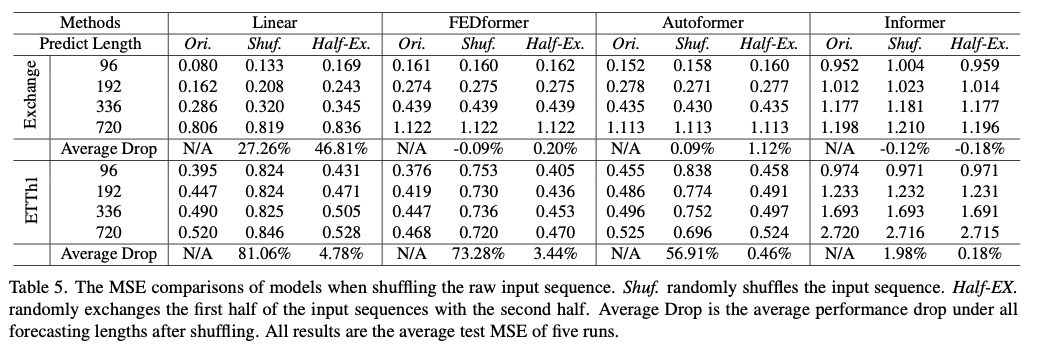
✔️ 전체적으로 LTSF-Linear 모델들이 Transformer 기반 모델들보다 평균적인 성능 하락이 모든 경우에 컸으며, 이는 Transformers 기반 모델들이 temporal order
를 잘 보존하지 않는 것을 나타냄
💡 How effective are different embedding strategies?
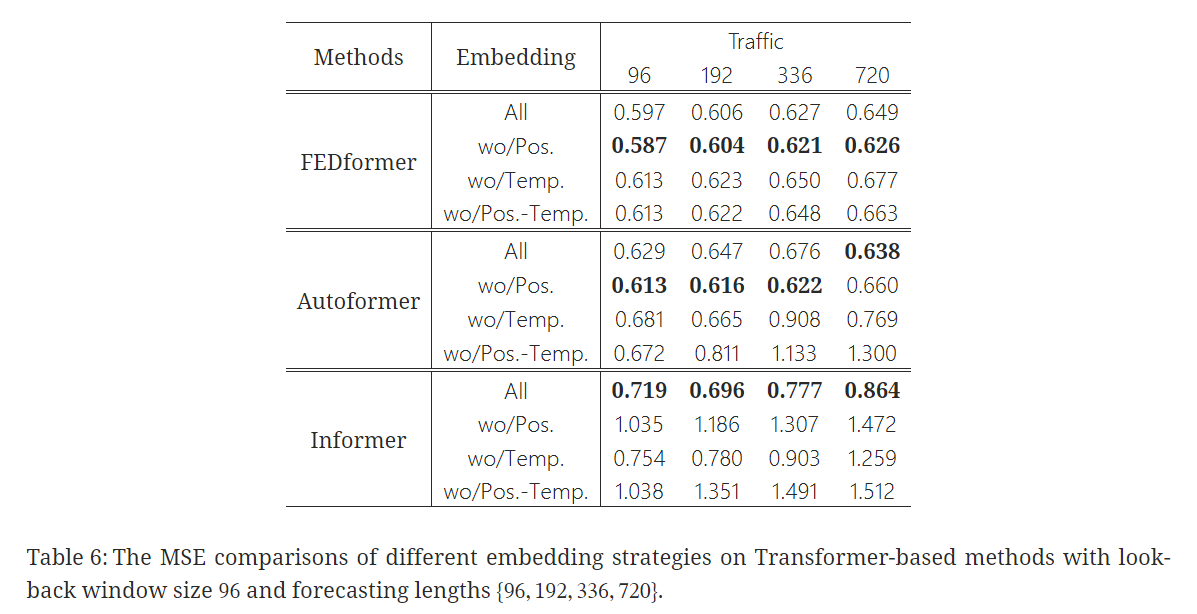
- Transformer 기반 모델들에서 사용된 position & timestamp embeddings의 이점에 대해 확인
✔️ Informer는 positional embeddings가 없을 경우 예측 오류가 크게 증가
++++timestamp embeddings가 없는 경우에는 예측 길이가 길어짐에 따라 성능이 점차 하락
++++ Informer가 각 토큰에 대해 단일 time step을 사용하기 때문에 temporal information을 토큰에 도입해야 함
✔️ FEDformer와 Autoformer는 각 토큰마다 단일 time step을 사용하지 않고 temporal information을 도입하기 위해 timestamps의 시퀀스를 입력
++++ 고정된 positional embeddings 없이도 비슷하거나 더 나은 성능을 달성
++++ global temporal information loss 때문에 timestamp embeddings이 없으면 Autoformer의 성능은 빠르게 하락
++++ FEDformer는 temporal inductive bias를 도입하기 위한 frequency-enhanced module 덕분에 position/timestamp embeddings을 제거해도 성능이 덜
하락
💡 Is training data size a limiting factor for existing LTSF-Transformers?
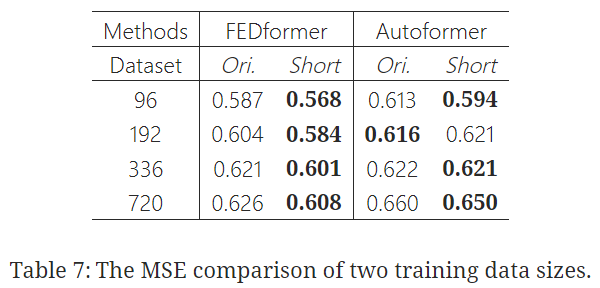
✔️ 기대와는 달리 실험 결과 더 작은 크기의 training data에서의 예측 오류가 더 작게 나옴
✔️ whole-year data가 더 길지만 불완전한 data size보다 더 분명한 temporal features를 유지하기 때문으로 보임
✔️ training을 위해 더 적은 데이터를 써야 한다고 결론지을 수는 없지만, 이는 Autoformer와 FEDformer의 training data scale이 성능에 제한을 주는 요인은 아니란 것을 증명
💡 Is efficiency really a top-level priority?
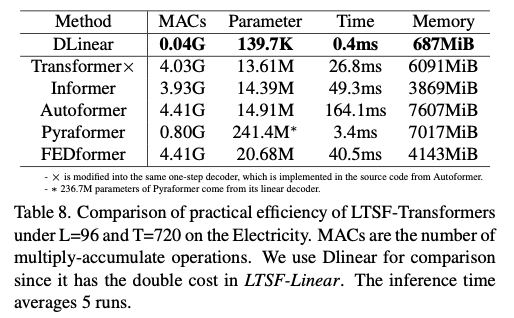
✔️ 흥미롭게도 vanilla Transformer(동일한 DMS decoder)와 비교했을 때, 대부분의 Transformer를 변형한 모델들의 실제 추론 시간과 파라미터의 개수는 비슷하거나 더 나쁨
✔️ 게다가 vanilla Transformer의 memory cost는 output length L = 720에서도 실질적으로 허용 가능한 수준이기 때문에 적어도 기존 벤치마크에서는 메모리 효울이 높은 Transformer의 개발의 중요성이 약화
6. Conclusion and Future Work
Conclusion
· 본 논문은 long-term time series forecasting 문제에서 Transformer 기반 모델들의 효과에 대한 의문을 제시
· 놀라울만큼 간단한 linear model인 LTSF-Linear 를 DMS forecasting baseline으로 삼아 본 논문의 주장을 검증
Future work
· LSTF-Linear는 모델 용량이 제한되어 있어 여러 문제점이 발생하며, 향후 연구의 기준선 역할을 할 뿐임
· one-layer linear network는 change points에 의해 발생하는 temporal dynamics를 포착하는 데 어려움이 있음
· 새로운 모델 설계와 데이터 전처리, 벤치마크 등을 통해 까다로운 LTSF 문제를 해결할 가능성이 있음
🔖 Reference
논문 리뷰
Transfomer 기반 TSF 모델 종류
