[자료구조] BBST

🎞️ BBST

Balanced Binary Search Tree, 균형 이진 탐색 트리: 왼쪽 서브트리와 오른쪽 서브트리의 height 차이가 1 이하인 이진트리

• 노드의 삽입/삭제 시에도 높이 차이를 유지해야 함
• 종류: Red-black 트리, AVL 트리

🎞️ Red-Black Tree

• 트리의 모든 노드는 레드 or 블랙
• Root 노드는 무조건 블랙
• 모든 단말노드는 블랙
• 루트 노드에서 단말 노드까지 블랙의 개수는 항상 같음
• 레드 노드의 자식은 모두 블랙
• 블랙 노드의 자식은 상관 없음

🎞️ Red-Black Tree 균형 유지 방법

Restructuring, Recoloring 연산

• 자신과 부모 노드가 레드일 때:
  • 삼촌 노드가 블랙이거나 Null이면: Restructuring
    • 1. 나와 내 부모, 내 부모의 부모를 오름차순으로 정렬
    • 2. 가운데 값을 부모로 만들고 나머지 둘을 자식으로 만듬
    • 3. 올라간 가운데 값을 블랙, 두 자식을 레드로 만듬
  • 삼촌 노드가 레드면: Recoloring
    • 1. 새 노드와 부모와 삼촌을 블랙으로 변경하고, 부모의 부모 노드를 레드로 만듬
    • 2. 내 조상 노드가 root가 아니면 더블 레드 발생 가능성

🎞️ Red-Black Tree가 선호되는 이유

삽입/삭제 연산이 더 수월함

시간복잡도 성능이 더 좋음

🎞️ AVL Tree

• 이진 탐색 트리
• 왼쪽, 오른쪽 서브트리의 height은 최대 1 차이
• 높이 차이가 1보다 커지면 회전을 통해 균형 맞춤
• 삽입/검색/삭제 시간복잡도: O(log N)

Balance Factor - BF(K) = (K의 왼쪽 서브트리의 높이) - (K의 오른쪽 서브트리의 높이)

🎞️ AVL Tree 균형 유지 방법

Right Rotation (우회전)

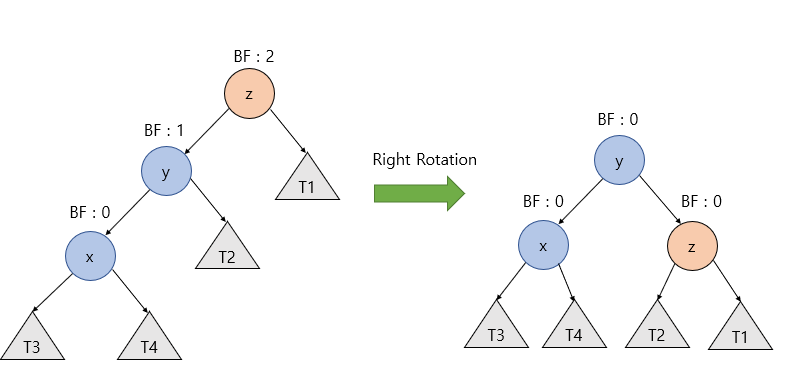
1. y 노드의 오른쪽 자식 노드를 z 노드로 변경
2. z 노드의 왼쪽 자식 노드를 y 노드의 오른쪽 서브트리로 변경

Left Rotation (좌회전)

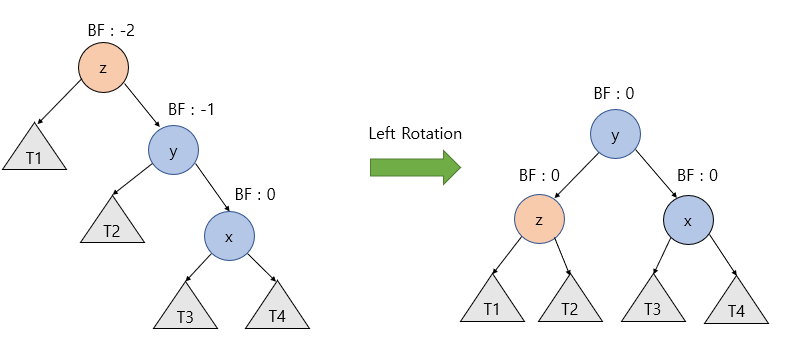
1. y 노드의 왼쪽 자식 노드를 z 노드로 변경
2. z 노드의 오른쪽 자식 노드를 y 노드의 왼쪽 서브트리로 변경

Left Left Case (LL) - 우회전 적용

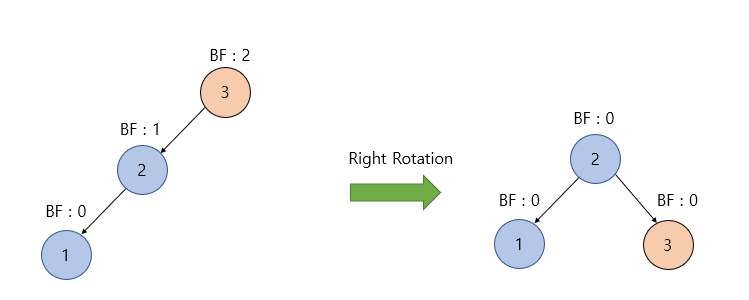
Right Right Case (RR) - 좌회전 적용

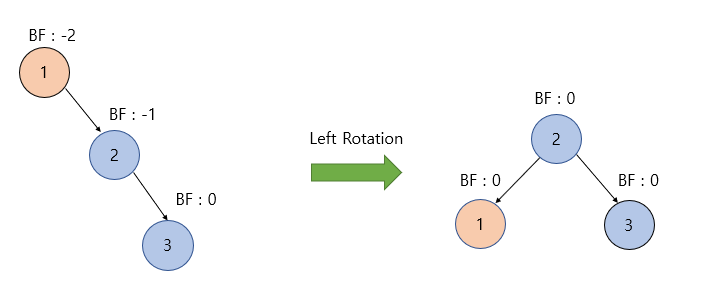
Left Right Case (LR) - 좌회전 > 우회전

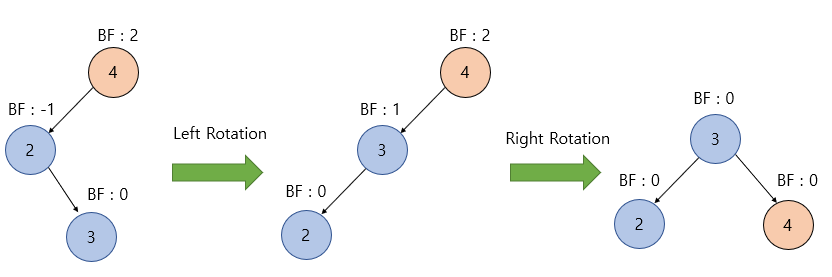
Right Left Case (RL) - 우회전 > 좌회전

---

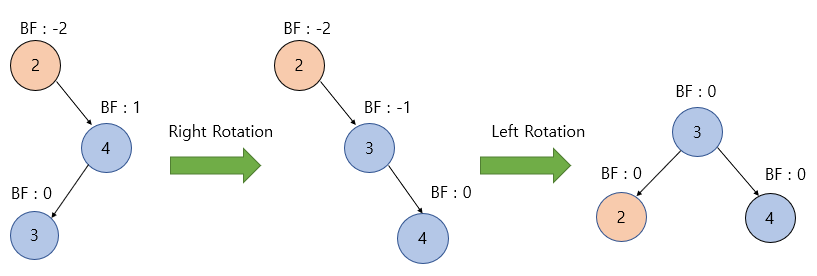
참고:

• [자료구조] 레드-블랙 트리(Red-Black Tree)란? | 레드-블랙 트리 쉽게 이해하기