[자료구조] 문자열 저장 자료구조/알고리즘

🎞️ Trie

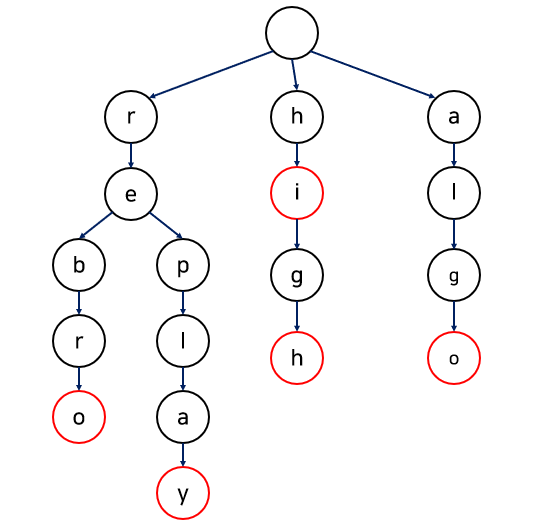
Trie: 문자열 저장/탐색을 위한 트리 형태의 자료구조

• DFS으로 검색하면 단어 찾을 수 있음
• 루트 노드: 비어있음
• 나머지 노드: 집합에 포함된 문자열의 prefix부터 시작해서 서브트리로 문자열 형성
• 리프 노드: 문자열의 끝을 나타냄

장점: 문자열 탐색/삽입이 빠름

• 삽입: O(N)
  • 이미 존재하는 문자열과 겹치면 문자열의 길이만큼 노드를 따라가서 글자를 추가
  • 아예 겹치지 않으면 추가하는 문자열 길이만큼 추가

단점: 필요한 메모리가 너무 큼

• 문자열이 모두 영소문자로 구성됐다 해도 자식 노드를 가리키는 26개의 포인터를 저장해야 함
• 최악의 경우, 집합에 포함되는 문자열들의 길이의 총합만큼 노드가 필요함
  • 총 메몰: O(포인터 크기 포인터 배열 개수 총 노드 개수)

구현

public class Trie {
	class Node {
    	Map<Character, Node> childNode = new HashMap<Character, Node>();
        boolean endOfWord;
    }
    Node = rootNode = new Node();
    
    void insert(String str) {
    	Node node = this.rootNode;
        for (int i = 0; i < str.length(); i++) {
        	node = node.childNode.computeIfAbsent(str.charAt(i), key -> new Node());
        }
        node.endOfWord = true;
    }
    
    boolean search(String str) {
    	Node node = this.rootNode;
        for (int i = 0; i < str.length(); i++) {
        	node = node.childNode.getOrDefault(str.charAt(i), null);
            if (node == null) {
            	return false;
            }
        }
        return node.endOfWord;
}

🎞️ KMP

접두사(prefix)와 접미사(suffix)의 개념을 활용해 모든 경우를 계산하지 않고 반복되는 연산을 줄여나가 매칭 문자열을 빠르게 점프하는 기법

과정

• 1. 부분 일치 테이블 준비
  • 부분 일치 테이블: 접두사와 접미사가 되는 문자열의 최대 길이를 저장하는 테이블
• 2. 문자열 맨 앞부분은 begin, matched = 0부터 탐색
  • matched: 일치하는 문자열의 수
• 3. 만약 pattern과 parent의 해당 글자가 일치하면 matched 카운트 증가
• 4. 만약 matched 카운트와 pattern 총 길이가 일치하면 답에 추가
• 5. pattern과 parent의 해당 글자가 일치하지 않을 때
  • matched가 0이면 다음칸에서 계속
  • begin의 위치 옮김
    • 옮겼다고 처음부터 다시 비교할 필요는 없음

🎞️ Rabin Karp

문자열에 해싱 기법을 사용해 해시 값으로 비교하는 알고리즘

• 간단하게 해시 값을 만들려면 문자열의 각 문자(ASCII 테이블 값)에 특정 수의 제곱수를 차례대로 곱하여 모두 더하면 됨

검색 과정: 지정한 수 (검색 대상 문자열 해시 값 - 맨 앞의 문자열 값 지정한 수^제곱 수) + 새로 탐색된 문자열 값

public void findString(String original, string search) {
	int originalSize = original.length();
    int searchSize = search.length();
    
    int originalHash = 0;
    int searchHash = 0;
    int power = 1;
    
    for (in ti = 0; i <= originalSize - searchSize; i++) {
    	if (i == 0) {
        	for (int j = 0; j < searchSize; j++) {
            	originalHash =+ original[searchSize - 1 - j] * power;
                searchHash += search[searchSize - 1 - j] * power;
                if (j < searchSize -1) {
                	power *= 3;
                }
            }
        } else {
        	originalHash = 3 * (originalHash - original[i-1] * power) + original[searchSize - 1 + i];
        }
        
        if (originalHash == searchHash) {
        	boolean found = true;
            
            for (int j = 0; j < searchSize; j++) {
            	if (original[i + j] != saerch[j]) {
                	found = false;
                    break;
                }
            }
            
            if (found) {
            	return (i+1)
            }
        }
    }
}

---

참고:

• [자료구조] 트라이(Trie) 자료구조
• [Algorithm] Trie를 Java로 구현해보자
• [알고리즘] 문자열 매칭 알고리즘 KMP (Java)
• [알고리즘] 라빈-카프 알고리즘 (Rabin-Karp)